Solutions for Sample Final Exam
- Page ID
- 6267
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\[\mathbf{BioSci\: 102,\\ Sample\: Study\: Problems\: for\: Final\: Exam}\]
1. To determine the \(\mathrm{K_{m}}\) and \(\mathrm{k_{cat}}\) (= turnover number) of an enzyme, 0.1 nmole of enzyme was added to substrate at various concentrations and the appearance of product was measured.
When the substrate concentration was \(\mathrm{1 \times 10^{-5}\: M}\), the product formed by:
15 seconds was 0.5 \(\mu\)mole
30 seconds was 1.0 \(\mu\)mole
45 seconds was 1.5 \(\mu\)mole
\[\mathbf{V=2\mu mol/min\: (or\: 33\: nmol/sec)}\]
\[\mathbf{\dfrac{1}{V}=0.5\: min/\mu mol,\: \dfrac{1}{[S]}=10^{5}\: M^{-1}}\]
When the substrate concentration was \(\mathrm{2\times 10^{-5}\: M}\), the product formed by:
15 seconds was 0.75 \(\mu\)mole
30 seconds was 1.5 \(\mu\)mole
45 seconds was 2.25 \(\mu\)mole
\[\mathbf{V=3\mu mol/min\: (or\: 50\: nmol/sec)}\]
\[\mathbf{\dfrac{1}{V}=0.33\: min/ \mu mol, \: \dfrac{1}{[S]}=5\times 10^{4}\: M^{-1}}\]
When the substrate concentration was \(\mathrm{4\times 10^{-5}\: M}\), the product formed by:
15 seconds was 1.0 \(\mu\)mole
30 seconds was 2.0 \(\mu\)mole
45 seconds was 3.0 \(\mu\)mole
\[\mathbf{V=4\mu mol/min\: (or\: 67\: nmol/sec)}\]
\[\mathbf{\dfrac{1}{V}=0.25\: min/ \mu mol,\: \dfrac{1}{[S]}=2.5\times 10^{4}\: M^{-1}}\]
When the substrate concentration was \(\mathrm{10\times 10^{-5}\: M}\), the product formed by:
15 seconds was 1.25 \(\mu\)mole
30 seconds was 2.5 \(\mu\)mole
45 seconds was 3.75 \(\mu\)mole
\[\mathbf{V=5\: \mu mol/min\: (or\: 83\: nmol/sec)}\]
\[\mathbf{\dfrac{1}{V}=0.20\: min/ \mu mol,\: \dfrac{1}{[S]}=10^{4}\: M^{-1}}\]
Using the supplied graph paper, and showing all work, calculate the \(\mathrm{K_{m}}\) and \(\mathrm{K_{cat}}\) for this enzyme.
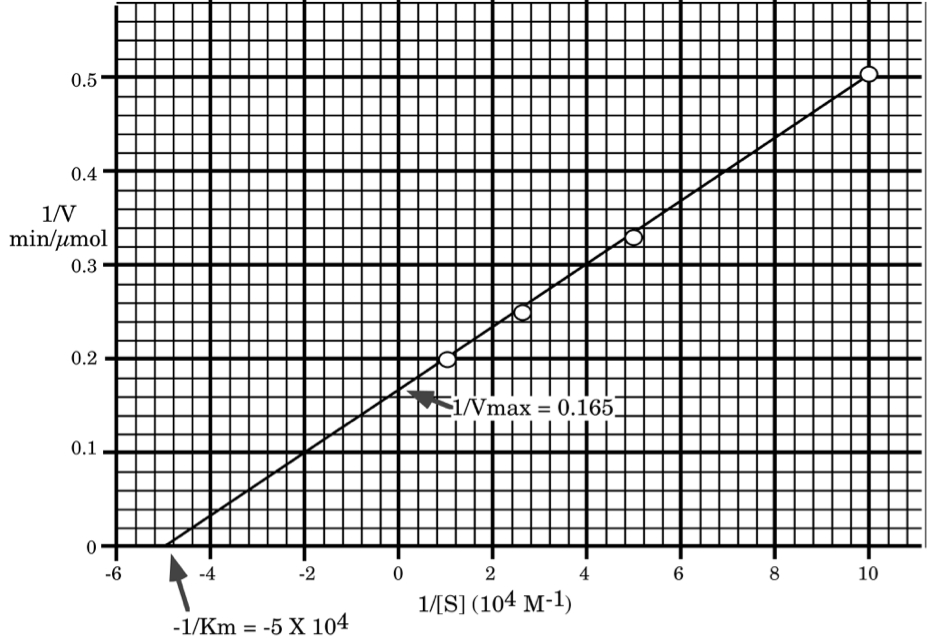
\[\mathbf{\dfrac{1}{V_{max}}=0.165\: sec/ \mu mole,\: V_{max}=6.1\: \mu mol/min\: (100\: nmol/sec)}\]
\[\mathbf{\dfrac{-1}{[K_{m}]}=-5\times 10^{4}\: M^{-1},\: [K_{m}]=2\times 10^{-5}\: M}\]
\[\mathbf{K_{cat}= \dfrac{V_{max}}{[E_{t}]}=\dfrac{6.1\: \mu mol/min}{10^{-4}\: \mu mol}=6.1\times 10^{4}\: min^{-1}\: (or\: 1,000/sec)}\]
\[\mathbf{check\: V_{max}\: and\: K_{m}\: to\: make\: sure\: we\: made\: no\: error.}\]
\[\mathbf{For\: [S]=10\: \mu M\: V=\dfrac{6.1\times 10}{20+10}=2.03\: (very\: close\: to\: 2)}\]
\[\mathbf{For\: [S]=100\: \mu M\: V=\dfrac{6.1\times 100}{20+100}=5.08\: (very\: close\: to\: 5)}\]
2. An enzyme was assayed at different concentrations of substrate in the presence and in the absence of an inhibitor. The initial velocities (\(\mathrm{\mu moles\: \times\: liter^{-1}\: \times min^{-1}}\)) were measured at various substrate concentrations (moles/liter) were plotted according to the Lineweaver-Burk method and the following plot was obtained.
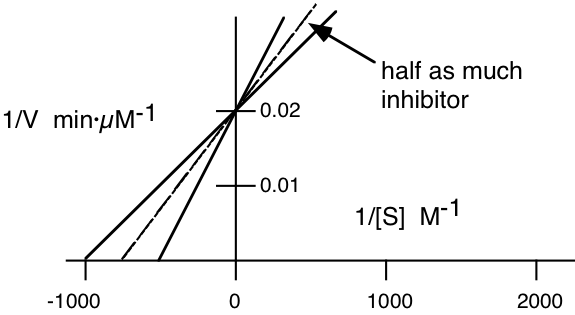
Answer the follow questions:
a) Label the X axis and the Y axis with the appropriate symbols and units.
b) What is the \(\mathrm{K_{m}}\) of the enzyme for the substrate in the absence of inhibitor?
\[\mathbf{-1/K_{m}=-1000\: M^{-1}}\]
\[\mathbf{K_{m}=10^{-3}\: M}\]
c) What is the \(\mathrm{V_{max}}\) of the enzyme solution in the absence of inhibitor?
\[\mathbf{1/V_{max}=0.02}\]
\[\mathbf{V_{max}=50\: \mu M/min}\]
d) On the graph above, sketch the plot that would be obtained if the amount of inhibitor were decreased to about half the amount originally used.
e) Write an equation which you could be used to determine the \(\mathrm{K_{i}}\) of the inhibitor from the above information.
\[\mathbf{Km_{app}\: (Km\: in\: the\: presence\: of\: inhibitor)=Km(1+\dfrac{[I]}{K_{I}}})\]
3. The \(\mathrm{K_{m}}\) for an enzyme catalyzed reaction is \(\mathrm{10^{-4}\: M}\). The apparent \(\mathrm{K_{m}}\) for the same reaction in the presence of \(\mathrm{9\times 10^{-5}\: M}\) inhibitor is \(\mathrm{10^{-3}\: M}\).
a) Is the binding of substrate to enzyme greater or less in the presence of inhibitor? Why?
\[\mathbf{Less.\: Km_{app}>Km\: so\: less\: binding\: when\: inhibitor\: present}\]
b) What is the \(\mathrm{K_{i}}\) for the inhibitor?
\[\mathbf{Km_{app}=Km(1+\dfrac{[I]}{K_{I}})}\]
\[\mathbf{10^{-3}=10^{-4}(1+\dfrac{9\times 10^{-5}}{K_{I}})}\]
\[\mathbf{(1+\dfrac{9\times 10^{-5}}{K_{I}})=10}\]
\[\mathbf{\dfrac{9\times 10^{-5}}{K_{I}}=9}\]
\[\mathbf{K_{I}=\dfrac{9\times 10^{-5}}{9}=10^{-5}}\]
c) How would \(\mathrm{V_{max}}\) without the inhibitor compare with \(\mathrm{V_{max}}\) with the inhibitor?
This must be a competitive inhibitor so \(\mathrm{V_{max}}\) will not change.
4. (12) An enzymatic reaction containing 5 nM enzyme is found to have a \(\mathrm{V_{max}}\) of 50 nM/min and a \(\mathrm{K_{m}}\) for substrate of \(\mathrm{4\times 10^{-5}\: M}\). If the enzyme is incubated with substrate at a concentration of \(\mathrm{4\times 10^{-5}\: M}\) what would be the concentration of the enzyme substrate (ES) complex once the steady state had been reached? Show your reasoning.
\[\mathbf{[ES]=\dfrac{[E_{t}][S]}{K_{m}+[S]}=\dfrac{5\times 10^{-9}\cdot 4\times 10^{-5}}{4\times 10^{-5}+4\times 10^{-5}}=2.5\: nM}\]
\[\mathbf{or,\: K_{m}=[S],\: so\: V=1/2\: V_{max},\: so\: k_{cat}[ES]=1/2k_{cat}[E_{t}],\\ so\: [ES]=1/2[E_{t}]=0.5\times 5\: nM=2.5\: nM}\]
5. The enzyme triose-phosphate isomerase catalyzes the interconversion of glyceraldehyde-3-phosphate (G-3-P) and dihydroxyacetone phosphate (DHAP). Which of the following factors influence the rate of this enzyme catalyzed reaction?
\(\mathrm{\Delta G^{\circ’}}\)
X [E] or enzyme concentration
X \(\mathrm{k_{cat}}\) or turnover number of the enzyme
X T (temperature)
\(\mathrm{K’_{eq}}\)
X [G-3-P]
6. Enzyme inhibitors can be classified into four types: Irreversible (I), Competitive (C), Non-competitive (N) and Uncompetitive (U). The following statements are valid for one or more of these four inhibitors. In the space to the left of each statement, indicate by letter (I, C, N, or U) for which inhibitors the statement is true. Indicate all correct answers for each!
I, C Addition of this inhibitor can lead to a decrease in the fraction of enzyme with a bound substrate molecule.
C In the presence of this inhibitor, the enzyme's affinity for the substrate appears to have decreased (versus the enzyme's affinity for the substrate in the absence of the inhibitor).
N, I In the presence of this inhibitor, the enzyme's affinity for the substrate is the same as in the inhibitors absence.
C, N, U This inhibitor can usually be removed from the enzyme by dialysis.
I, N, U The \(\mathrm{V_{max}}\) of the enzyme solution is decreased by this inhibitor.
C In the presence of this inhibitor the \(\mathrm{K_{m}}\) of the enzyme for its substrate is larger than the \(\mathrm{K_{m}}\) value measured for the same substrate in the absence of the inhibitor.
N, U This inhibitor can be bound to the enzyme while the substrate is also bound to the enzyme.
I This inhibitor cannot be removed from the enzyme by ion exchange chromatography.
7. The following types of bonds and interactions have been discussed throughout this course.
\[\begin{matrix} \mathrm{A)\: Hydrogen\: Bond}& \mathrm{D)\: Ionic\: interaction\: (salt\: bridge)}\\ \mathrm{B)\: Hydrophobic\: interactions}& \mathrm{E)\: Peptide\: bond}\\ \mathrm{C)\: Disulfide\: bond}& \: \end{matrix}\]
For each of the following statements, insert the letter of the one, most appropriate bond or interaction that is being described. (In these statements the word "bond" is used to represent bonds or interactions). A given letter may be used more than once.
B The "bond" that is disrupted by urea.
D The disruption of these "bonds" results in a change in \(\mathrm{pK_{a}}\) of hemoglobin after combination with oxygen.
A The "bond" responsible for stabilizing the \(\alpha\)-helix structure of proteins.
E The type of "bond" broken when asparagine is converted to aspartic acid.
8. One liter of a 0.2 M glycine buffer (\(\mathrm{pK_{a1}=2.34,\: pK_{a2}=9.60}\)) at pH 9.4 is titrated with 0.05 moles of HCl. What is the pH of the resulting solution?
\[\begin{matrix} \mathbf{start: \: 9.4=9.6+log\dfrac{[G^{-}]}{[G^{\circ}]}} & \mathbf{End: \: add\: 0.05\: M\: H^{+}}\\ \mathbf{=-0.2=log\dfrac{[G^{-}]}{[G^{\circ}]}}& \mathbf{[G^{\circ}]=0.12+0.05=0.17\: M}\\ \mathbf{[G^{-}]=0.63[G^{\circ}]}& \mathbf{[G^{-}]=0.08-0.05=0.03\: M}\\ \mathbf{0.63[G^{\circ}]+[G^{\circ}]=0.2\: M}& \mathbf{pH=9.6+log\dfrac{0.03}{0.17}}\\ \mathbf{1.63[G^{\circ}]=0.2\: M}& \mathbf{=8.85}\\ \mathbf{[G^{\circ}=0.12\: M}& \: \\ \mathbf{[G^{-}]=0.08\: M}& \: \end{matrix}\]
9. Consider the following peptides:
1. his ala pro pro tyr a pentapeptide
2. asn glu trp a tripeptide
3. tyr glu ala arg a tetrapeptide
a) Which would move further toward the anode (+) in electrophoresis at pH 7.0 (in the absence of SDS)? Why? What would its charge be at pH 7.0?
#2 would move most rapidly toward the anode because it would have the most negative charge.
The charge on #2 would be +1 -1 -1 = -1 (for N-term, glu side chain, C-term)
[Note charge on #1 is approximately +1 +0.1 -1 = +0.1 (N-term, his, C-term)
#3 is +1 -1 +1 -1 = 0 (N-term, glu, arg, C-term)]
b) Which would least likely be found in an \(\alpha\)-helix? Why?
#1 is least likely because of the presence of two proline residues that have a tendency to destabilize this structure.
c) Draw the structural formula for peptide #3 at pH = 7.
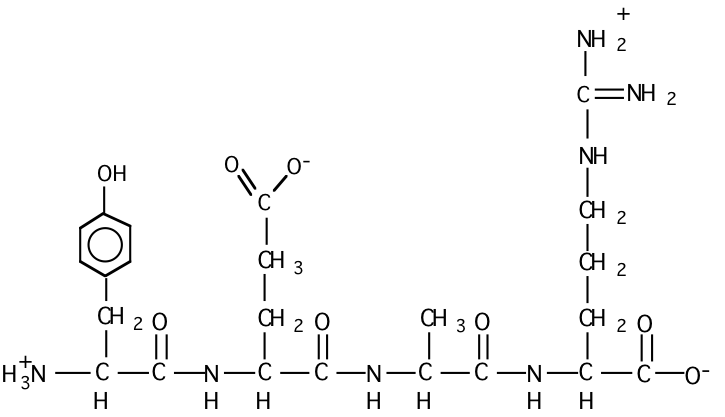
d) Which peptide would have the highest isoelectric point? Why?
Peptide #1
Why? Quick way - Peptide #2 is acidic so it has a low pI. In peptide #3 the N and C-term would essentially cancel each other, the Glu and Arg side chains would essentially cancel each other as well, and the pI would be near neutrality. For peptide #1 the N and C term would cancel, but the His would raise the pI to higher than neutral.
Or calculate all of the pIs:
\[\mathbf{Number\: 1}\: \begin{matrix} \: & \mathbf{2.2}&\: & \mathbf{6.0}&\: & \mathbf{9.2}& \: \\ \mathbf{+2}& \Leftrightarrow & \mathbf{+1}& \Leftrightarrow& \mathbf{0} &\Leftrightarrow & \mathbf{-1}\\ \: & \mathbf{C-term}& \: & \mathbf{His}& \: & \mathbf{N-term} &\: \end{matrix}\: \mathbf{etc. \: pI=(6.0+9.2)/2=7.6}\]
\[\mathbf{Number\: 2\: acidic\: so\: it\: is\: very\: negative}\]
\[\mathbf{Number\: 3}\: \begin{matrix} \: & \mathbf{2.2}& \: & \mathbf{4.2}& \: & \mathbf{9.0} &\: \\ \mathbf{+2}& \Leftrightarrow & \mathbf{+1}& \Leftrightarrow & \mathbf{0} & \Leftrightarrow & \mathbf{-1} \\ \: & \mathbf{C-term}& \: & \mathbf{Glu} & \: & \mathbf{N-term}& \: \end{matrix}\: \mathbf{etc.\: pI=(4.2+9.0)/2=6.6}\]
e) What would the one letter code for the three peptides be?
1) HAPPY
2) NEW
3) YEAR
10. Recently bacteria have been found living in thermal vents (temperatures of \(\mathrm{80^{\circ}C}\) and above) under the ocean. How might you expect the lipids in the membranes of such bacteria to differ from those of the bacteria in your own gut? Why?
Higher temperatures would favor longer, more saturated lipids in the membranes. This would maintain proper membrane fluidity/rigidity at the higher temperature. (Cholesterol would also help, but it is not usually present in prokaryotic membranes).
11. The \(\mathrm{\Delta G^{\circ’}}\) of hydrolysis of acetylphosphate to acetate and \(\mathrm{H_{3}PO_{4}}\) is -10 kcal/mole at pH 7 and \(\mathrm{25^{\circ}C}\). The \(\mathrm{\Delta G^{\circ’}}\) for hydrolysis of ATP to ADP and Pi is -7.3 kcal/mole under these same conditions.
a) Calculate the \(\mathrm{\Delta G^{\circ’}}\) and \(\mathrm{K’_{eq}}\) of the following reaction (give units of your answer).

\[\begin{matrix} \mathbf{AcPO_{4}+H_{2}O\rightarrow Ac+H_{3}PO_{4}}& \mathbf{\Delta G^{\circ’}=-10\: kcal/mol}\\ \mathbf{ADP+H_{3}PO_{4}\rightarrow ATP+H_{2}O}& \mathbf{\underline{+\Delta G^{\circ’}=+7.3\: kcal/mol}}\\ \: & \mathbf{ -2.7\: kcal/mol} \end{matrix}\]
\[\mathbf{\Delta G^{\circ’}=-RTlnK’_{eq}}\]
\[\mathbf{-2.7\: kcal/mol=-1.98\times 10^{-3}\: kcal/^{\circ}mol\cdot 298 k\: ln K’_{eq}}\]
\[\mathbf{lnK’_{eq}=\dfrac{-2.7\: kcal/mol}{-1.98\times 10^{-3}\: kcal/^{\circ} mol\cdot 298\:k}}\]
\[\mathbf{lnK’_{eq}=4.58}\]
\[\mathbf{K’_{eq}=97.5}\]
b) Assume the concentrations of both ATP and ADP are equal to 3.0 mM in the above reaction mixture and that \(\mathrm{CH_{3}CO_{2}^{-}}\) is at 5 mM. What concentration of acetylphosphate must be present in order for neither the forward nor the reverse reaction to be thermodynamically favored?
at equilibrium neither reaction is favored, so answer by determining the equilibrium concentration
\[\mathbf{K’_{eq}=\dfrac{[ATP][Ac]}{[ADP][AcP]}}\]
\[\mathbf{97.5=\dfrac{3\times 10^{-3}\cdot 5\times 10^{-3}}{3\times 10^{-3}\cdot [AcP]}}\]
\[\mathbf{[AcP]=\dfrac{5\times 10^{-3}}{97.5}=5.15\times 10^{-5}\: M\: or\: 51.3\: \mu M}\]
12. For the items below place the symbol "<" (less than), ">" (greater than), "=" (equal) or "?" (cannot say from information given) in the space to indicate the relationship between the two quantities. (e. g. amount of DNA in a human cell > amount of DNA in E. coli cell). Note: MW is abbreviation for molecular weight. (2 pts each).
a) ten H-bonds < one covalent bond (e. g. C–C)
b) charge on His at pH 7.0 > charge on His at pH 8.0
c) charge on Tyr in solution > charge on Asp in the same solution
d) charge on Tyr in solution ? charge on Asp in a different solution
e) MW of amino acid I = MW of Leu
f) MW of Trp = MW of amino acid W
g) One hundred H-bonds > one covalent bond (e. g. C–C)
h) MW of amino acid E > MW of amino acid D
13. A solution of tubulin monomers is warmed to \(\mathrm{37^{\circ}C}\), and the following change in light scattering (measured by \(\mathrm{A_{340}}\)) is observed:

Explain what is happening at time points "A", "B", and "C".
A. Lag phase - no nucleation has occured so tublin is not yet polymerizing
B. Some nucleation events have occured and tubulin monomers add rapidly to form microtubules.
C. [monomers] has decreased to a level where monomer addition rate is equal to the rate of depolymerization – steady state reached (treadmilling).
14. Under one set of conditions the following constants apply to the rate of subunit addition and loss from the two ends of actin filaments:
| + end | - end | |
|---|---|---|
| \(\mathrm{k_{on}\: (\mu M^{-1}S^{-1})}\) | 11.6 | 1.3 |
| \(\mathrm{k_{off}\: (S^{-1})}\) | 1.4 | 0.8 |
Assuming that actin filaments are present in solution at time zero, determine if there will be a net increase or decrease in the length of the filaments over time under the following conditions:
a) 1.0 \(\mu\)M actin monomers
\[\mathbf{\dfrac{dn^{+}}{dt}=11.6\cdot 1-1.4=+10.2\: sec^{-1}}\]
\[\mathbf{\dfrac{dn^{-}}{dt}=1.3\cdot 1-0.8=+0.5\: sec^{-1}}\]
\[\mathbf{net=10.7\: sec^{-1},\underline{\: net\: increase}}\]
b) 0.5 \(\mu\)M actin monomers
\[\mathbf{\dfrac{dn^{+}}{dt}=11.6\cdot 0.5-1.4=+4.4\: sec^{-1}}\]
\[\mathbf{\dfrac{dn^{-}}{dt}=1.3\cdot 0.5-0.8=-0.15\: sec^{-1}}\]
\[\mathbf{net=4.25\: sec^{-1},\: \underline{net\: increase}}\]
c) 0.1 \(\mu\)M actin monomers
\[\mathbf{\dfrac{dn^{+}}{dt}=11.6\cdot 0.1-1.4=-0.24\: sec^{-1}}\]
\[\mathbf{\dfrac{dn^{-}}{dt}=1.3\cdot 0.1-0.8=-0.67\: sec^{-1}}\]
\[\mathbf{net=-0.91\: sec^{-1},\: \underline{net\: decrease}}\]
d) Which, if any of the above answers would be changed if all of the actin filaments present at the beginning of the experiment are modified so that no subunit addition or loss can occur from their minus ends?
No change, a and b still positive, c still negative
15. The compound tosyl-phenylalaninechloromethyl ketone (TPCK, below) is an affinity ligand for chymotrypsin.

a) (10) Draw the structure of a similar affinity ligand that would be appropriate for trypsin.
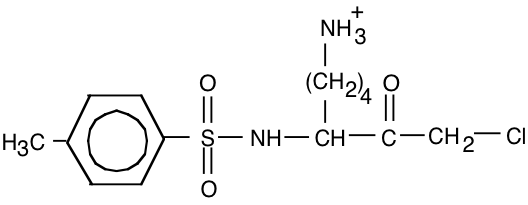
Replace “Y” with “K” or “R”.
b) (8) How would you test the affinity ligand you have drawn to see if it has the desired properties?
Add it to a sample of trypsin and compare the activity of this sample to a control sample without added "inhibitor" (by testing for ability to digest a protein or peptide). Inhibition would be a first indication that the reagent worked. Next, a sample of trypsin + inhibitor could be hydrolyzed and the hydrolysate could be analyzed to see if an amino acid had been modified by attachment of the inhibitor molecule.
16.
a) What forces and interactions are responsible for binding the substrate of chymotrypsin to the active site. Explain.
Primarily hydrogen bonds and hydrophobic interactions. The substrate polypeptide chain is held in a groove on the surface of chymotrypsin by a series of hydrogen bonds in a structure resembling an anti-parallel \(\beta\)-pleated sheet. The aromatic residue of the substrate polypeptide where the chymotrypsin will cleave is held in the "hydrophobic pocket" by hydrophobic interactions to position the substrate properly for cleavage.
b) Give an example of a change in the substrate binding site of chymotrypsin (as in a mutation which results in one amino acid being substituted for another) that would alter how tightly the enzyme binds substrate. Indicate whether it would increase or decrease the affinity of the enzyme for substrate.
A hydrophobic amino acid in the hydrophobic pocket could be replaced by a charged AA. This would reduce the binding of the substrate. (one example of many possible)
c) Give an example as in b) except that the mutation would change the activity of the enzyme but not binding. Explain your answer.
The Asp in the catalytic triade could be replced by a Glu. This would change the position of the acid group, reducing the catalytic activity of the enzyme. The \(\mathrm{k_{cat}}\) would be decreased, but the \(\mathrm{K_{m}}\) would not necessarily change.

