6.5: ATP- Adenosine Triphosphate
- Page ID
- 75465
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Explain the role of ATP as the cellular energy currency
- Describe how energy is released through hydrolysis of ATP
Even exergonic, energy-releasing reactions require a small amount of activation energy in order to proceed. However, consider endergonic reactions, which require much more energy input, because their products have more free energy than their reactants. Within the cell, where does energy to power such reactions come from? The answer lies with an energy-supplying molecule called adenosine triphosphate, or ATP. ATP is a small, relatively simple molecule (Figure \(\PageIndex{1}\)), but within some of its bonds, it contains the potential for a quick burst of energy that can be harnessed to perform cellular work. This molecule can be thought of as the primary energy currency of cells in much the same way that money is the currency that people exchange for things they need. ATP is used to power the majority of energy-requiring cellular reactions.
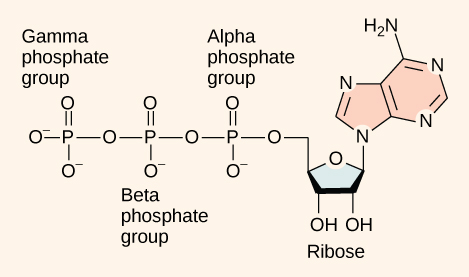
As its name suggests, adenosine triphosphate is comprised of adenosine bound to three phosphate groups (Figure \(\PageIndex{1}\)). Adenosine is a nucleoside consisting of the nitrogenous base adenine and a five-carbon sugar, ribose. The three phosphate groups, in order of closest to furthest from the ribose sugar, are labeled alpha, beta, and gamma. Together, these chemical groups constitute an energy powerhouse. However, not all bonds within this molecule exist in a particularly high-energy state. Both bonds that link the phosphates are equally high-energy bonds (phosphoanhydride bonds) that, when broken, release sufficient energy to power a variety of cellular reactions and processes. These high-energy bonds are the bonds between the second and third (or beta and gamma) phosphate groups and between the first and second phosphate groups. The reason that these bonds are considered “high-energy” is because the products of such bond breaking—adenosine diphosphate (ADP) and one inorganic phosphate group (Pi)—have considerably lower free energy than the reactants: ATP and a water molecule. Because this reaction takes place with the use of a water molecule, it is considered a hydrolysis reaction. In other words, ATP is hydrolyzed into ADP in the following reaction:
\[\ce{ATP + H_2O \rightarrow ADP + P_{i} + free\: energy} \nonumber\]
Like most chemical reactions, the hydrolysis of ATP to ADP is reversible. The reverse reaction regenerates ATP from ADP + Pi. Indeed, cells rely on the regeneration of ATP just as people rely on the regeneration of spent money through some sort of income. Since ATP hydrolysis releases energy, ATP regeneration must require an input of free energy. The formation of ATP is expressed in this equation:
\[\ce{ADP + P_{i} + free\: energy \rightarrow ATP + H_2O} \nonumber\]
Two prominent questions remain with regard to the use of ATP as an energy source. Exactly how much free energy is released with the hydrolysis of ATP, and how is that free energy used to do cellular work? The calculated ∆G for the hydrolysis of one mole of ATP into ADP and Pi is −7.3 kcal/mole (−30.5 kJ/mol). Since this calculation is true under standard conditions, it would be expected that a different value exists under cellular conditions. In fact, the ∆G for the hydrolysis of one mole of ATP in a living cell is almost double the value at standard conditions: 14 kcal/mol (−57 kJ/mol).
ATP is a highly unstable molecule. Unless quickly used to perform work, ATP spontaneously dissociates into ADP + Pi, and the free energy released during this process is lost as heat. The second question posed above, that is, how the energy released by ATP hydrolysis is used to perform work inside the cell, depends on a strategy called energy coupling. Cells couple the exergonic reaction of ATP hydrolysis with endergonic reactions, allowing them to proceed. One example of energy coupling using ATP involves a transmembrane ion pump that is extremely important for cellular function. This sodium-potassium pump (Na+/K+ pump) drives sodium out of the cell and potassium into the cell (Figure 6.4.2). A large percentage of a cell’s ATP is spent powering this pump, because cellular processes bring a great deal of sodium into the cell and potassium out of the cell. The pump works constantly to stabilize cellular concentrations of sodium and potassium. In order for the pump to turn one cycle (exporting three Na+ ions and importing two K+ ions), one molecule of ATP must be hydrolyzed. When ATP is hydrolyzed, its gamma phosphate doesn’t simply float away, but is actually transferred onto the pump protein. This process of a phosphate group binding to a molecule is called phosphorylation. As with most cases of ATP hydrolysis, a phosphate from ATP is transferred onto another molecule. In a phosphorylated state, the Na+/K+ pump has more free energy and is triggered to undergo a conformational change. This change allows it to release Na+ to the outside of the cell. It then binds extracellular K+, which, through another conformational change, causes the phosphate to detach from the pump. This release of phosphate triggers the K+ to be released to the inside of the cell. Essentially, the energy released from the hydrolysis of ATP is coupled with the energy required to power the pump and transport Na+ and K+ ions. ATP performs cellular work using this basic form of energy coupling through phosphorylation.

Often during cellular metabolic reactions, such as the synthesis and breakdown of nutrients, certain molecules must be altered slightly in their conformation to become substrates for the next step in the reaction series. One example is during the very first steps of cellular respiration, when a molecule of the sugar glucose is broken down in the process of glycolysis. In the first step of this process, ATP is required for the phosphorylation of glucose, creating a high-energy but unstable intermediate. This phosphorylation reaction powers a conformational change that allows the phosphorylated glucose molecule to be converted to the phosphorylated sugar fructose. Fructose is a necessary intermediate for glycolysis to move forward. Here, the exergonic reaction of ATP hydrolysis is coupled with the endergonic reaction of converting glucose into a phosphorylated intermediate in the pathway. Once again, the energy released by breaking a phosphate bond within ATP was used for the phosphorylation of another molecule, creating an unstable intermediate and powering an important conformational change.
Summary
ATP is the primary energy-supplying molecule for living cells. ATP is made up of a nucleotide, a five-carbon sugar, and three phosphate groups. The bonds that connect the phosphates (phosphoanhydride bonds) have high-energy content. The energy released from the hydrolysis of ATP into ADP + Pi is used to perform cellular work. Cells use ATP to perform work by coupling the exergonic reaction of ATP hydrolysis with endergonic reactions. ATP donates its phosphate group to another molecule via a process known as phosphorylation. The phosphorylated molecule is at a higher-energy state and is less stable than its unphosphorylated form, and this added energy from the addition of the phosphate allows the molecule to undergo its endergonic reaction.
Review Questions
The energy released by the hydrolysis of ATP is
- primarily stored between the alpha and beta phosphates
- equal to −57 kcal/mol
- harnessed as heat energy by the cell to perform work
- providing energy to coupled reactions
- Answer
-
Answer: D
Which of the following molecules is likely to have the most potential energy?
- sucrose
- ATP
- glucose
- ADP
- Answer
-
Answer: A
Free Response
Do you think that the EA for ATP hydrolysis is relatively low or high? Explain your reasoning.
- Answer
-
Answer: The activation energy for hydrolysis is very low. Not only is ATP hydrolysis an exergonic process with a large −∆G, but ATP is also a very unstable molecule that rapidly breaks down into ADP + Pi if not utilized quickly. This suggests a very low EA since it hydrolyzes so quickly.
Study Figure \(\PageIndex{2}\). The hydrolysis of one ATP molecule releases 7.3 kcal/mol of energy (∆G = −7.3 kcal/mol of energy). If it takes 2.1 kcal/mol of energy to move one Na+ across the membrane (∆G = +2.1 kcal/mol of energy), how many sodium ions could be moved by the hydrolysis of one ATP molecule?
- Answer
-
Answer: Three sodium ions could be moved by the hydrolysis of one ATP molecule. The ∆G of the coupled reaction must be negative. Movement of three sodium ions across the membrane will take 6.3 kcal of energy (2.1 kcal × 3 Na+ ions = 6.3 kcal). Hydrolysis of ATP provides 7.3 kcal of energy, more than enough to power this reaction. Movement of four sodium ions across the membrane, however, would require 8.4 kcal of energy, more than one ATP molecule can provide.
Glossary
- ATP
- adenosine triphosphate, the cell’s energy currency
- phosphoanhydride bond
- bond that connects phosphates in an ATP molecule
Contributors and Attributions
Connie Rye (East Mississippi Community College), Robert Wise (University of Wisconsin, Oshkosh), Vladimir Jurukovski (Suffolk County Community College), Jean DeSaix (University of North Carolina at Chapel Hill), Jung Choi (Georgia Institute of Technology), Yael Avissar (Rhode Island College) among other contributing authors. Original content by OpenStax (CC BY 4.0; Download for free at http://cnx.org/contents/185cbf87-c72...f21b5eabd@9.87).



