By now you should realize the similarities among the chemical and mathematical equations used to describe binding, facilitated diffusion, and enzyme kinetics of macromolecule interactions with ligands and substrates. In simple, noncooperative systems, it all starts with a macromolecule, usually a protein, binding a ligand, which can be a small molecule or another macromolecule.
\[M+L \rightleftharpoons ML\]
In some cases, the only function of M is to bind and release ligand (as in the case of myoglobin). In other cases, the ligand is transformed. In the simplest case involving transformation, the ligand is moved across a membrane down a concentration gradient (facilitated diffusion), a purely physical step.
\[R+A_{out} \rightleftharpoons RA \rightarrow R + A_{in}\]
In a yet more complicated case, the ligand can be transformed chemically (enzyme kinetics) into product.
\[E+S \rightleftharpoons ES \rightarrow E + P\]
In this chapter we added interactions (multiple substrates, inhibitors) and saw that the basic form of the binding, facilitated diffusion, and enzyme kinetic equations and graphs for noncooperative system were extremely similar since the biological function always depended in some fashion on the concentration of the macromolecule complex ( ML, RA, ES, EI, ESI etc). The PowerPoint below reviews the similarity in the results of the mathematical analyses and resulting graphs showing the concentration dependencies of complex formation, facilitated diffusion, and enzyme-catalyzed chemical reactions.
- PowerPoint: Summary of Graphical Descriptions of Noncooperative Binding, Facilitated Diffusion, and Enzyme Kinetics
A feel for the dissociation constant
In all of the curves shown in the above PowerPoint, a ligand concentration can be found at which the biological effect is half maximum (either activation or inhibition of a biological function). Remember, only in certain conditions is that number equal to the dissociation constant for ligand. This is clearly the case when the only interaction is a 1:1 binding of a macromolecule and ligand. If an inhibitor was unknowingly present during the direct or indirect measurement of a binding reaction, the ligand concentration at half-maximal binding would equal the apparent Kd, not the actual dissociation constant. In the case of facilitated diffusion and enzyme-catalyzed chemical transformation of a single substrate, the ligand concentration at half-maximal binding is equal to the dissociation constant only in the rapid equilibrium assumption holds. It clearly doesn't in the steady state assumption, and clearly not in more complicated systems. Consider the case when a ligand binds a neurotransmitter receptor and alters intracellular the calcium ion concentration through a complicated signal transduction system. If the step leading to the releases of stored intracellular calcium is several steps removed from the actual binding of ligand to a neurotransmitter receptor, the likelihood that the ligand concentration at half-maximal increase in intracellular calcium is equal to the Kd for ligand binding is small. If however, the actual ligand dissociation constant for the receptor can be determined (using radiolabeled ligand, for example), and it is equal to the ligand concentration for half-maximal calcium increase, then it might be argued the binding is "rate or effect determining". When inhibitors of biological function are used, IC50 values (the inhibitor concentration at which the response is reduced to 50%) are usually reported.
From the Simple to the Complex
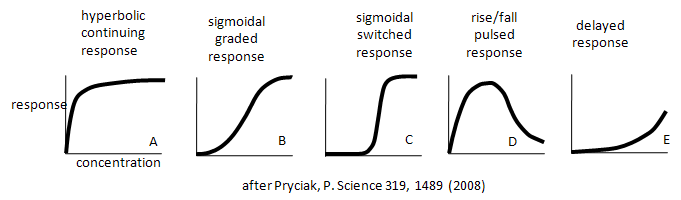
Enzymes don't work in isolation. Most are part of complex synthetic/degradative or signal transduction systems in which their biological response (product formation or degradation, pathway regulation, etc.) are functions of ligand concentration and are subject to signals further upstream or downstream in their resident pathways. How are the dose responses for biological activity modulated by other parts of the pathway? Although the equations we've derived don't directly predict the responses in lieu of knowing the concentrations, rate constants, and dissociation constants for all the steps in the pathway, an approach based on simple assumptions might illuminate the possibilities. A recent paper by Bashor et al and an analysis of it by Pryciak describe the input and output responses of signaling enzymes attached "in series" to a scaffold protein and how different dose responses outputs can be engineered to meet the requirements of the pathway. Examples of different dose-response curves from Bashor analysis are shown below. We've actually seen many of these response curves for individual protein/enzymes or chemical reaction systems. Curve A represents a typical response curve which could be produced by a process governed by a simple \(M + L \rightleftharpoons ML\) equilibrium. Curves B and C are sigmoidal and could be produced by a process governed by a multisubunit enzyme following the MWC model with different values for the parameters L and c. Curve D is similar to the output of consecutive irreversible reactions such as \(A \rightarrow B \rightarrow C\), where the response would be similar to the rise and fall B with time (not concentration, however). One could envision a dose/response, however, that could produce a rise/fall as in curve D. Likewise Curve E would reflect the rise of C in the same chemical reaction. To a first approximation, one could image that the responses shown below are produced by steps that are rate-limiting in the overall pathway such that the overall response is governed by those steps. Obviously a complex mathematical systems analysis involving the solving of matrices of differential equations for each step would be required for a more realistic understanding of actual biological responses, but I hope you can see that an understanding of real biological networks must start with a kinetic and thermodynamic understanding of the "simple" steps that constitute larger system pathways.
Contributors and Attributions



