Many enzymes do not demonstrate hyperbolic saturation kinetics, or typical Michaelis-Menten kinetics. Graphs of initial velocity vs substrate demonstrate sigmoidal dependency of \(v\) on \(S\), much as we discussed with hemoglobin binding of dioxygen. Enzymes that display this non Michaelis-Menten behavior have common characteristics. They:
- are multi-subunit
- bind other ligands at sites other than the active site (allosteric sites)
- can be either activated or inhibited by allosteric ligands
- exist in two major conformational states, \(R\) and \(T\)
- often control key reactions in major pathways, which must be regulated.
A classic examples of allosterically regulated enzymes includes glycogen phosphorylase which breaks down intracellular glycogen reserves.
 Glycogen Phosphorylase
Glycogen Phosphorylase
Aspartate Transcarbamyolase
Another is aspartate transcarbamyolase, which catalyzes the first step in the synthesis of pyrimidine nucleotides. CTP is an allosteric inhibitor of this enzyme, which makes physiological sense since high levels of this pyrimidine nucleotide should inhibit the first enzyme in the synthesis of pyrimidines. ATP is a allosteric activator. This also makes sense since if high levels of the purine nucleotide ATP are present, one would also want to balance the level of pyrimidine nucleotides.
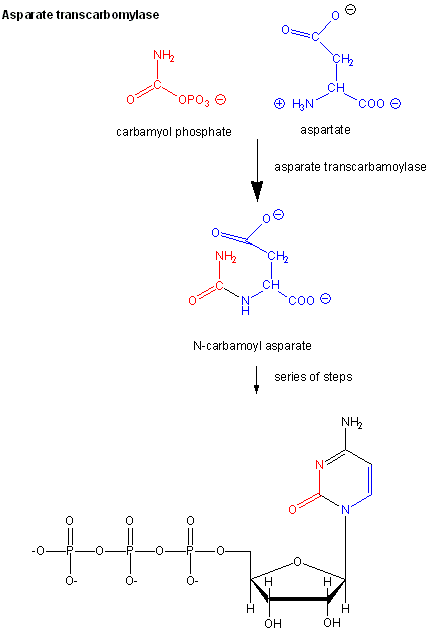
Figure \(\PageIndex{1}\): Aspartate transcarbamoylase: reactions
Earlier we saw that cooperative binding equilibrium could be modeled with the Hill Equation, which was introduced through the equation
\[Y = L^n/(K_d + L^n) = L^n/(P_{50}^n + L^n)\]
where n is the cooperativity or Hill Coefficient. Likewise, for an enzyme which demonstrates cooperative (sigmoidal) initial rates plots,
\[v_o = \dfrac{V_mS^n}{K {0.50}^n + L^n} \]
When \(n=1\), the equation reduces to the classical hyperbolic Michaelis Menten equation. For values of n>1, sigmoidal plots are observed. We found a more easily understandable molecular interpretation of cooperative binding of oxygen to hemoglobin using the MWC model (T and R states). The MWC model has also been applied successfully to multi-subunit enzymes which display cooperative, sigmoidal kinetics. In this model, allosteric inhibitors (which often don't resemble the substrate) bind preferentially to the T state, leading to lower activity, while allosteric activators bind preferentially to the R state, leading to greater activity. Activators shift the vo vs S curve to the left while inhibitors shift it to the right (much like protons and carbon dioxide in hemoglobin binding). These allosteric ligands induce their effects by shifting the To <=> Ro equilibrium.
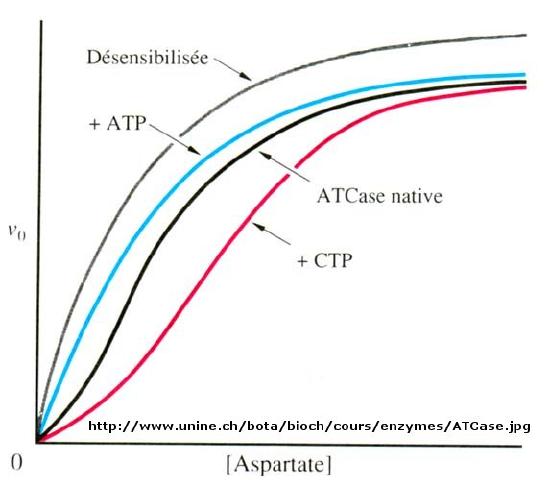
Figure \(\PageIndex{2}\): spartate transcarbamoylase: Non Michaelis-Menten Kinetics
How Do Allosteric Effectors Change \(V_m\) and \(Km\)?
We have just studied how competitive, uncompetitive, and noncompetitive (or mixed) inhibitors influence the apparent \(Km\) and \(V_m\) values for enzymes that display Michaelis-Menten kinetics.How are \(V_m\) and \(Km\) influenced in allosteric enzymes? The example given above (ATCase), analogous to effects observed in hemoglobin:oxgyen binding, influence the apparent \(Km\), but not the \(V_m\). Remember that in the case of hemoglobin binding curves, the allosteric activators and effectors we discussed shifted the sigmoidal binding curves to the left or right, but all reached a plateau at the same fractional saturation value of 1. Allosteric enzyme systems that behave like this are called K systems.
Enzymes in which allosteric regulators change \(V_m\), called V systems, are also known. V systems display hyperbolic \(v_o\) vs. \(S\) curves in which activators display a greater apparent \(V_m\) and inhibitors display a lower \(V_m\) without affecting the apparent \(Km\).In these systems, both the T and R forms have the same affinity for substrate (hence the same apparent \(K_m\)).This would be analogous to a situation in the MWC model where KR/KT =1 which also gave hyperbolic, not sigmoidal Y vs. a curves. This difference in V systems is that the R and T states have different catalytic rate constants, \(k_cat\), for turnover of the bound substrate (hence different apparent \(V_m\) values).In addition, the activator A and inhibitor I bind to the R and T forms with different affinity, which again shifts the \(T_o \rightleftharpoons R_o\) equilibrium in the presence of the allosteric effectors.
Cooperative binding of dioxygen to hemoglobin, regulated by allosteric effectors (protons and carbon dioxide), was ideal for an oxygen transport system which must load and unload oxygen over a narrow range of oxygen concentrations and allosteric effectors. Allosteric enzymes are usually positioned at key metabolic steps which can be regulated to activate or inhibit whole pathways.
Enzyme Regulation by Covalent Modification
Many enzymes are regulated not by allosteric ligands (activators and inhibitors), but by covalent modification. Often the covalent modification involves phosphorylation (by enzymes called kinases which transfer a phosphate from ATP to a Ser, Thr, or Tyr on the target enzyme) or phosphatases (which remove the phosphates from phospho-Ser, Thr, or Tyr in the target protein). In fact 1-2% of all genes in the human genome code for kinases and phosphatases.
Contributors and Attributions




