16.5: The Action Potential
- Page ID
- 34543
- Describe the components of the membrane that establish the resting membrane potential
- Describe the changes that occur to the membrane that result in the action potential
The functions of the nervous system—sensation, integration, and response—depend on the functions of the neurons underlying these pathways. To understand how neurons are able to communicate, it is necessary to describe the role of an excitable membrane in generating these signals. The basis of this communication is the action potential, which demonstrates how changes in the membrane can constitute a signal. Looking at the way these signals work in more variable circumstances involves a look at graded potentials, which will be covered in the next section.
Electrically Active Cell Membranes
Most cells in the body make use of charged particles, ions, to build up a charge across the cell membrane. Previously, this was shown to be a part of how muscle cells work. For skeletal muscles to contract, based on excitation–contraction coupling, requires input from a neuron. Both of the cells make use of the cell membrane to regulate ion movement between the extracellular fluid and cytosol.
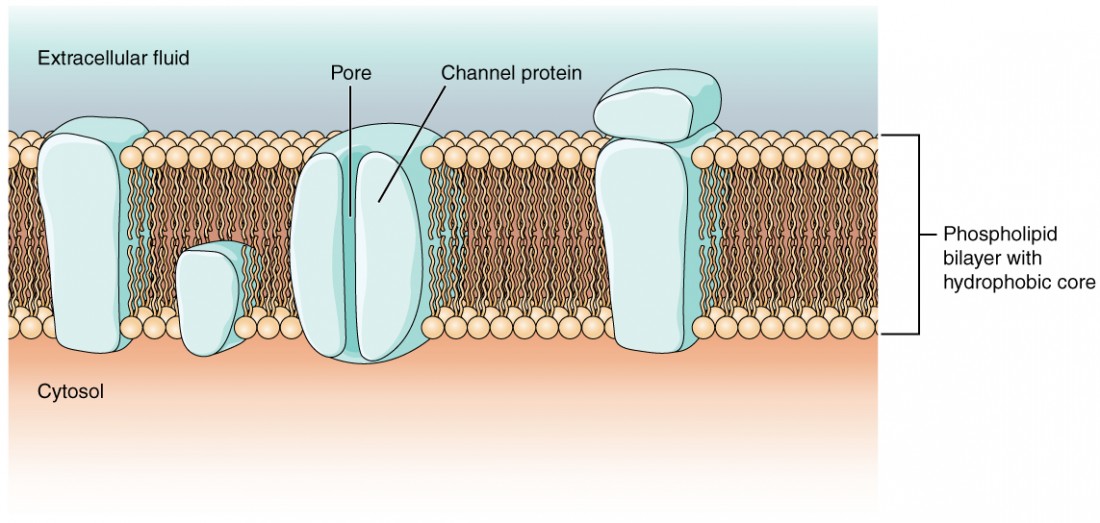
As you learned in the chapter on cells, the cell membrane is primarily responsible for regulating what can cross the membrane and what stays on only one side. The cell membrane is a phospholipid bilayer, so only substances that can pass directly through the hydrophobic core can diffuse through unaided. Charged particles, which are hydrophilic by definition, cannot pass through the cell membrane without assistance (Figure 1). Transmembrane proteins, specifically channel proteins, make this possible. Several channels, as well as specialized energy dependent “ion-pumps,” are necessary to generate a transmembrane potential and to generate an action potential. Of special interest is the carrier protein referred to as the sodium/potassium pump that moves sodium ions (Na+) out of a cell and potassium ions (K+) into a cell, thus regulating ion concentration on both sides of the cell membrane.
The sodium/potassium pump requires energy in the form of adenosine triphosphate (ATP), so it is also referred to as an ATPase. As was explained in the cell chapter, the concentration of Na+ is higher outside the cell than inside, and the concentration of K+ is higher inside the cell is higher than outside. That means that this pump is moving the ions against the concentration gradients for sodium and potassium, which is why it requires energy. In fact, the pump basically maintains those concentration gradients.
Ion channels are pores that allow specific charged particles to cross the membrane in response to an existing concentration gradient. Proteins are capable of spanning the cell membrane, including its hydrophobic core, and can interact with the charge of ions because of the varied properties of amino acids found within specific domains or regions of the protein channel. Hydrophobic amino acids are found in the domains that are apposed to the hydrocarbon tails of the phospholipids. Hydrophilic amino acids are exposed to the fluid environments of the extracellular fluid and cytosol. Additionally, the ions will interact with the hydrophilic amino acids, which will be selective for the charge of the ion. Channels for cations (positive ions) will have negatively charged side chains in the pore. Channels for anions (negative ions) will have positively charged side chains in the pore. This is called electrochemical exclusion, meaning that the channel pore is charge-specific.
Ions can also be specified by the diameter of the pore. The distance between the amino acids will be specific for the diameter of the ion when it dissociates from the water molecules surrounding it. Because of the surrounding water molecules, larger pores are not ideal for smaller ions because the water molecules will interact, by hydrogen bonds, more readily than the amino acid side chains. This is called size exclusion. Some ion channels are selective for charge but not necessarily for size, and thus are called a nonspecific channel. These nonspecific channels allow cations—particularly Na+, K+, and Ca2+—to cross the membrane, but exclude anions.
Ion channels do not always freely allow ions to diffuse across the membrane. They are opened by certain events, meaning the channels are gated. So another way that channels can be categorized is on the basis of how they are gated. Although these classes of ion channels are found primarily in cells of nervous or muscular tissue, they also can be found in cells of epithelial and connective tissues.
A ligand-gated channel opens because a signaling molecule, a ligand, binds to the extracellular region of the channel. This type of channel is also known as an ionotropic receptor because when the ligand, known as a neurotransmitter in the nervous system, binds to the protein, ions cross the membrane changing its charge (Figure 2).

A mechanically gated channel opens because of a physical distortion of the cell membrane. Many channels associated with the sense of touch (somatosensation) are mechanically gated. For example, as pressure is applied to the skin, these channels open and allow ions to enter the cell. Similar to this type of channel would be the channel that opens on the basis of temperature changes, as in testing the water in the shower (Figure 3).

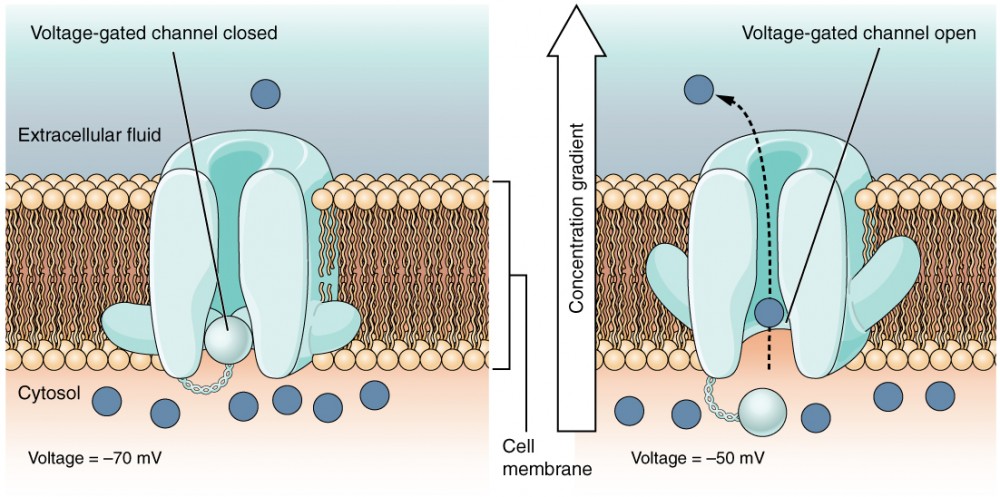
A voltage-gated channel is a channel that responds to changes in the electrical properties of the membrane in which it is embedded. Normally, the inner portion of the membrane is at a negative voltage. When that voltage becomes less negative, the channel begins to allow ions to cross the membrane (Figure 4).
A leakage channel is randomly gated, meaning that it opens and closes at random, hence the reference to leaking. There is no actual event that opens the channel; instead, it has an intrinsic rate of switching between the open and closed states. Leakage channels contribute to the resting transmembrane voltage of the excitable membrane (Figure 5).

The Membrane Potential
The electrical state of the cell membrane can have several variations. These are all variations in the membrane potential. A potential is a distribution of charge across the cell membrane, measured in millivolts (mV). The standard is to compare the inside of the cell relative to the outside, so the membrane potential is a value representing the charge on the intracellular side of the membrane based on the outside being zero, relatively speaking (Figure 6).

The concentration of ions in extracellular and intracellular fluids is largely balanced, with a net neutral charge. However, a slight difference in charge occurs right at the membrane surface, both internally and externally. It is the difference in this very limited region that has all the power in neurons (and muscle cells) to generate electrical signals, including action potentials.
Before these electrical signals can be described, the resting state of the membrane must be explained. When the cell is at rest, and the ion channels are closed (except for leakage channels which randomly open), ions are distributed across the membrane in a very predictable way. The concentration of Na+ outside the cell is 10 times greater than the concentration inside. Also, the concentration of K+ inside the cell is greater than outside. The cytosol contains a high concentration of anions, in the form of phosphate ions and negatively charged proteins. Large anions are a component of the inner cell membrane, including specialized phospholipids and proteins associated with the inner leaflet of the membrane (leaflet is a term used for one side of the lipid bilayer membrane). The negative charge is localized in the large anions.
With the ions distributed across the membrane at these concentrations, the difference in charge is measured at −70 mV, the value described as the resting membrane potential. The exact value measured for the resting membrane potential varies between cells, but −70 mV is most commonly used as this value. This voltage would actually be much lower except for the contributions of some important proteins in the membrane. Leakage channels allow Na+ to slowly move into the cell or K+ to slowly move out, and the Na+/K+ pump restores them. This may appear to be a waste of energy, but each has a role in maintaining the membrane potential.
The Action Potential
Resting membrane potential describes the steady state of the cell, which is a dynamic process that is balanced by ion leakage and ion pumping. Without any outside influence, it will not change. To get an electrical signal started, the membrane potential has to change.
This starts with a channel opening for Na+ in the membrane. Because the concentration of Na+ is higher outside the cell than inside the cell by a factor of 10, ions will rush into the cell that are driven largely by the concentration gradient. Because sodium is a positively charged ion, it will change the relative voltage immediately inside the cell relative to immediately outside. The resting potential is the state of the membrane at a voltage of −70 mV, so the sodium cation entering the cell will cause it to become less negative. This is known as depolarization, meaning the membrane potential moves toward zero.
The concentration gradient for Na+ is so strong that it will continue to enter the cell even after the membrane potential has become zero, so that the voltage immediately around the pore begins to become positive. The electrical gradient also plays a role, as negative proteins below the membrane attract the sodium ion. The membrane potential will reach +30 mV by the time sodium has entered the cell.
As the membrane potential reaches +30 mV, other voltage-gated channels are opening in the membrane. These channels are specific for the potassium ion. A concentration gradient acts on K+, as well. As K+ starts to leave the cell, taking a positive charge with it, the membrane potential begins to move back toward its resting voltage. This is called repolarization, meaning that the membrane voltage moves back toward the −70 mV value of the resting membrane potential.
Repolarization returns the membrane potential to the −70 mV value that indicates the resting potential, but it actually overshoots that value. Potassium ions reach equilibrium when the membrane voltage is below −70 mV, so a period of hyperpolarization occurs while the K+ channels are open. Those K+ channels are slightly delayed in closing, accounting for this short overshoot.

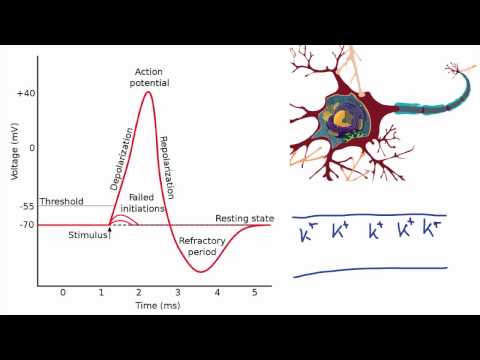
What has been described here is the action potential, which is presented as a graph of voltage over time in Figure 7. It is the electrical signal that nervous tissue generates for communication. The change in the membrane voltage from −70 mV at rest to +30 mV at the end of depolarization is a 100-mV change. That can also be written as a 0.1-V change.
To put that value in perspective, think about a battery. An AA battery that you might find in a television remote has a voltage of 1.5 V, or a 9-V battery (the rectangular battery with two posts on one end) is, obviously, 9 V. The change seen in the action potential is one or two orders of magnitude less than the charge in these batteries. In fact, the membrane potential can be described as a battery. A charge is stored across the membrane that can be released under the correct conditions. A battery in your remote has stored a charge that is “released” when you push a button.
What happens across the membrane of an electrically active cell is a dynamic process that is hard to visualize with static images or through text descriptions. View this animation to learn more about this process.
What is the difference between the driving force for Na+ and K+? And what is similar about the movement of these two ions?
The question is, now, what initiates the action potential? The description above conveniently glosses over that point. But it is vital to understanding what is happening. The membrane potential will stay at the resting voltage until something changes. The description above just says that a Na+ channel opens. Now, to say “a channel opens” does not mean that one individual transmembrane protein changes. Instead, it means that one kind of channel opens. There are a few different types of channels that allow Na+ to cross the membrane. A ligand-gated Na+ channel will open when a neurotransmitter binds to it and a mechanically gated Na+ channel will open when a physical stimulus affects a sensory receptor (like pressure applied to the skin compresses a touch receptor). Whether it is a neurotransmitter binding to its receptor protein or a sensory stimulus activating a sensory receptor cell, some stimulus gets the process started. Sodium starts to enter the cell and the membrane becomes less negative.
A third type of channel that is an important part of depolarization in the action potential is the voltage-gated Na+ channel. The channels that start depolarizing the membrane because of a stimulus help the cell to depolarize from −70 mV to −55 mV. Once the membrane reaches that voltage, the voltage-gated Na+ channels open. This is what is known as the threshold. Any depolarization that does not change the membrane potential to −55 mV or higher will not reach threshold and thus will not result in an action potential. Also, any stimulus that depolarizes the membrane to −55 mV or beyond will cause a large number of channels to open and an action potential will be initiated.
Because of the threshold, the action potential can be likened to a digital event—it either happens or it does not. If the threshold is not reached, then no action potential occurs. If depolarization reaches −55 mV, then the action potential continues and runs all the way to +30 mV, at which K+ causes repolarization, including the hyperpolarizing overshoot. Also, those changes are the same for every action potential, which means that once the threshold is reached, the exact same thing happens. A stronger stimulus, which might depolarize the membrane well past threshold, will not make a “bigger” action potential. Action potentials are “all or none.” Either the membrane reaches the threshold and everything occurs as described above, or the membrane does not reach the threshold and nothing else happens. All action potentials peak at the same voltage (+30 mV), so one action potential is not bigger than another. Stronger stimuli will initiate multiple action potentials more quickly, but the individual signals are not bigger. Thus, for example, you will not feel a greater sensation of pain, or have a stronger muscle contraction, because of the size of the action potential because they are not different sizes.
As we have seen, the depolarization and repolarization of an action potential are dependent on two types of channels (the voltage-gated Na+ channel and the voltage-gated K+ channel). The voltage-gated Na+ channel actually has two gates. One is the activation gate, which opens when the membrane potential crosses −55 mV. The other gate is the inactivation gate, which closes after a specific period of time—on the order of a fraction of a millisecond. When a cell is at rest, the activation gate is closed and the inactivation gate is open. However, when the threshold is reached, the activation gate opens, allowing Na+ to rush into the cell. Timed with the peak of depolarization, the inactivation gate closes. During repolarization, no more sodium can enter the cell. When the membrane potential passes −55 mV again, the activation gate closes. After that, the inactivation gate re-opens, making the channel ready to start the whole process over again.
The voltage-gated K+ channel has only one gate, which is sensitive to a membrane voltage of −50 mV. However, it does not open as quickly as the voltage-gated Na+ channel does. It might take a fraction of a millisecond for the channel to open once that voltage has been reached. The timing of this coincides exactly with when the Na+ flow peaks, so voltage-gated K+ channels open just as the voltage-gated Na+ channels are being inactivated. As the membrane potential repolarizes and the voltage passes −50 mV again, the channel closes—again, with a little delay. Potassium continues to leave the cell for a short while and the membrane potential becomes more negative, resulting in the hyperpolarizing overshoot. Then the channel closes again and the membrane can return to the resting potential because of the ongoing activity of the non-gated channels and the Na+/K+ pump.

All of this takes place within approximately 2 milliseconds (Figure 8). While an action potential is in progress, another one cannot be initiated. That effect is referred to as the refractory period. There are two phases of the refractory period: the absolute refractory period and the relative refractory period. During the absolute phase, another action potential will not start. This is because of the inactivation gate of the voltage-gated Na+ channel. Once that channel is back to its resting conformation (less than −55 mV), a new action potential could be started, but only by a stronger stimulus than the one that initiated the current action potential. This is because of the flow of K+ out of the cell. Because that ion is rushing out, any Na+ that tries to enter will not depolarize the cell, but will only keep the cell from hyperpolarizing.
Plotting voltage measured across the cell membrane against time (as shown in Figure 8), the events of the action potential can be related to specific changes in the membrane voltage.
- At rest, the membrane voltage is −70 mV.
- The membrane begins to depolarize when an external stimulus is applied.
- The membrane voltage begins a rapid rise toward +30 mV.
- The membrane voltage starts to return to a negative value.
- Repolarization continues past the resting membrane voltage, resulting in hyperpolarization.
- The membrane voltage returns to the resting value shortly after hyperpolarization.
Propagation of the Action Potential
The action potential is initiated at the beginning of the axon, at what is called the initial segment. There is a high density of voltage-gated Na+ channels so that rapid depolarization can take place here. Going down the length of the axon, the action potential is propagated because more voltage-gated Na+ channels are opened as the depolarization spreads. This spreading occurs because Na+ enters through the channel and moves along the inside of the cell membrane. As the Na+ moves, or flows, a short distance along the cell membrane, its positive charge depolarizes a little more of the cell membrane. As that depolarization spreads, new voltage-gated Na+ channels open and more ions rush into the cell, spreading the depolarization a little farther.
Because voltage-gated Na+ channels are inactivated at the peak of the depolarization, they cannot be opened again for a brief time—the absolute refractory period. Because of this, depolarization spreading back toward previously opened channels has no effect. The action potential must propagate toward the axon terminals; as a result, the polarity of the neuron is maintained, as mentioned above.
Propagation, as described above, applies to unmyelinated axons. When myelination is present, the action potential propagates differently. Sodium ions that enter the cell at the initial segment start to spread along the length of the axon segment, but there are no voltage-gated Na+ channels until the first node of Ranvier. Because there is not constant opening of these channels along the axon segment, the depolarization spreads at an optimal speed. The distance between nodes is the optimal distance to keep the membrane still depolarized above threshold at the next node. As Na+ spreads along the inside of the membrane of the axon segment, the charge starts to dissipate. If the node were any farther down the axon, that depolarization would have fallen off too much for voltage-gated Na+ channels to be activated at the next node of Ranvier. If the nodes were any closer together, the speed of propagation would be slower.
Propagation along an unmyelinated axon is referred to as continuous conduction; along the length of a myelinated axon, it is saltatory conduction. Continuous conduction is slow because there are always voltage-gated Na+ channels opening, and more and more Na+ is rushing into the cell. Saltatory conduction is faster because the action potential basically jumps from one node to the next (saltare = “to leap”), and the new influx of Na+ renews the depolarized membrane. Along with the myelination of the axon, the diameter of the axon can influence the speed of conduction. Much as water runs faster in a wide river than in a narrow creek, Na+-based depolarization spreads faster down a wide axon than down a narrow one. This concept is known as resistance and is generally true for electrical wires or plumbing, just as it is true for axons, although the specific conditions are different at the scales of electrons or ions versus water in a river.
Glial cells, especially astrocytes, are responsible for maintaining the chemical environment of the CNS tissue. The concentrations of ions in the extracellular fluid are the basis for how the membrane potential is established and changes in electrochemical signaling. If the balance of ions is upset, drastic outcomes are possible.
Normally the concentration of K+ is higher inside the neuron than outside. After the repolarizing phase of the action potential, K+ leakage channels and the Na+/K+ pump ensure that the ions return to their original locations. Following a stroke or other ischemic event, extracellular K+ levels are elevated. The astrocytes in the area are equipped to clear excess K+ to aid the pump. But when the level is far out of balance, the effects can be irreversible.
Astrocytes can become reactive in cases such as these, which impairs their ability to maintain the local chemical environment. The glial cells enlarge and their processes swell. They lose their K+ buffering ability and the function of the pump is affected, or even reversed. If a Na+ gradient breaks down, this has a more important effect than interrupting the action potential. Glucose transport into cells is coupled with Na+ co-transport. When that is lost, the cell cannot get the energy it needs. In the central nervous system, carbohydrate metabolism is the only means of producing ATP. Elsewhere in the body, cells rely on carbohydrates, lipids, or amino acids to power mitochondrial ATP production. But the CNS does not store lipids in adipocytes (fat cells) as an energy reserve. The lipids in the CNS are in the cell membranes of neurons and glial cells, notably as an integral component of myelin. Proteins in the CNS are crucial to neuronal function, in roles such as channels for electrical signaling or as part of the cytoskeleton. Those macromolecules are not used to power mitochondrial ATP production in neurons.
Contributors and Attributions
- Anatomy & Physiology. Authored by: OpenStax College. Provided by: Rice University. Located at: http://cnx.org/contents/14fb4ad7-39a1-4eee-ab6e-3ef2482e3e22@9.1. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/14fb4ad7-39a...f2482e3e22@9.1