Skip to main content
Biology LibreTexts

10.2: Modelling Predator-Prey Interactions

  1. Last updated
  2. Save as PDF
  • Page ID
    73113

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    This material in this chapter has been adapted from Donovan and Welden (2002). 

    Donovan, T. M. and C. Welden. 2002. Spreadsheet exercises in ecology and evolution. Sinauer Associates, Inc. Sunderland, MA, USA.

     

     

    PREDATOR-PREY DYNAMICS

    Objectives

    • Develop a model for the interactions between predators and their prey.

    • Understand how variation in prey demographic rates, predator demographic rates, and predator attack rates influence the population growth of predators and their prey.

     

    INTRODUCTION

    In this chapter, we will explore the classic Lotka-Volterra predator-prey model (Rosenzweig and MacArthur 1963), which treats each population as if it were growing exponentially.

     clipboard_e67891232b2017bdfaebc41b6aebd4fc4.png

     

    The Classical Lotka-Volterra Predator-Prey Model

    In the classic Lotka-Volterra model, neither prey population nor predator population has an explicit carrying capacity. However, either or both may have an implicit carrying capacity imposed by the interaction between the two populations.

     

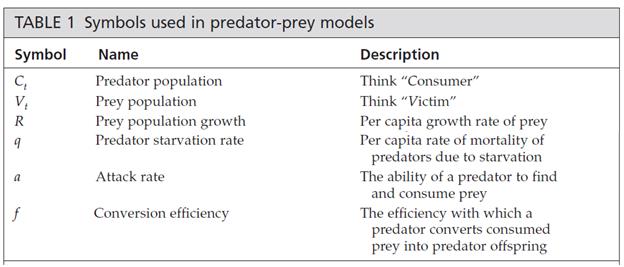
    To model the prey population, we begin with a basic geometric model for the prey population

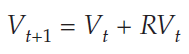
    clipboard_eb679815fa605a94a98541b190f62a987.png

    and subtract the number of prey individuals killed by predators in the interval from t  to t + 1. This number killed will depend on the number of predators: the more predators, the more prey they will kill. It will also depend on the number of prey available: the more prey, the more successful the predators. Finally, it will depend on the attack rate: the ability of a predator to find and consume prey. The number of prey killed in one time interval will be the product of these, or using the symbols given above, aCtVt. The equation for the prey population thus becomes

    clipboard_ec693ed7f9ee30410891392fe718b5fd5.png

    In words, the prey population grows according to its per capita growth rate minus losses to predators. Losses are determined by attack rate, predator population, and prey population.

     

    To model the predator population, we also begin with an exponential model, in concept. However, there is a wrinkle in this model, because we cannot assume a constant per capita rate of population growth. There is no simple R for the predator population because its growth rate will depend on how many prey are caught. As in the prey model, the number of prey caught will be aCtVt. The growth of the predator population will depend on this number, and on the efficiency with which predators convert consumed prey into predator offspring. We will represent this conversion efficiency with the parameter f, so the per capita population growth of predators will be afVtCt. We should reduce this predator population growth by some quantity to represent the starvation rate of predators who fail to consume prey. This will be the product of the per capita starvation rate times the predator population: qCt. Taking all this into account, we can write an equation for the predator population:

    clipboard_eafd12d0ebe2d22872589e4925d42e64e.png

    In words, the predator population grows according to the attack rate, conversion efficiency, and prey population, minus losses to starvation. Note that the product afVt acts as the predator’s R.

     

    Having created these models, we can ask several questions about the interaction they portray, such as

    • Under what conditions (i.e., parameter values) will the predator population drive the prey to extinction?

    • Under what conditions will the predator population die off, leaving the prey population to expand unhindered?

    • Under what conditions will predator and prey populations both persist indefinitely? What will be their population dynamics while they coexist? In other words, will one or both populations stabilize, or will they continue to change over time?

     

    Equilibrium Solutions

    As we did for the Interspecific Competition model, we will begin to answer these questions by seeking equilibrium solutions to Equations 1 and 2. For the prey population, we want to find values of predator and prey population sizes at which the prey population remains stable. In other words, we want to solve for ΔVt = 0.

    Beginning with Equation 1

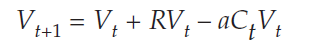
    clipboard_efdeefc40262f534fcc2a947eab7222c7.png

    we subtractVt from both sides, and get

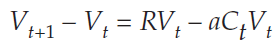
    clipboard_ecc6b8ae3cbb0965ac49a987af2668c11.png

    Because Vt+1 – Vt = ΔVt we can substitute into the equation and get

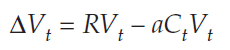
    clipboard_e2e681eeb9bd390163160cfc36f0ad0aa.png

    We are looking for a solution when ΔVt = 0, so we substitute again:

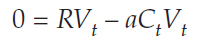
    clipboard_e319dd21606cb1482f95fff6ccc4d9024.png

    Adding aCtVt to both sides gives us

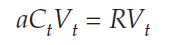
    clipboard_e0881c9550aef861ecb0b294454e0bb2d.png

    Dividing both sides byVt, we get

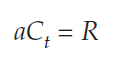
    clipboard_ef8ce6cde398a810170988bb57f387456.png

    Dividing both sides by a gives us our solution:

    clipboard_e8722f9034075acf5aa4486f5f2f2e195.png

    In words, the prey population reaches equilibrium when the predator population equals the prey’s per capita growth rate divided by the predator’s attack rate. Note that this is a constant. Strangely, the equilibrium size of the prey population is not determined by this solution, which says, in effect, that the prey population can be stable at any size as long as the predator population is at the specified size. 

     

    For the predator population, we follow the same strategy, and solve for ΔC = 0. Beginning with Equation 2,

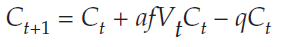
    clipboard_ee5b5ce03fd8a8bae030422a45acf4668.png

    we subtract Ct  from both sides, and get

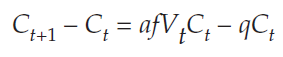
    clipboard_e31d7bb2569e298ba855ce888bb75ea97.png

    Because Ct+1 – Ct = ΔCt, we can substitute into the equation and get

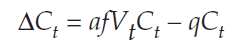
    clipboard_e99ef6fbbd84f32e07e1fcc20f7942e9e.png

    We are looking for a solution when ΔCt = 0, so we substitute again:

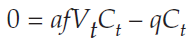
    clipboard_e4867be7f22cc548e798591c99c384599.png

    Adding qCt to both sides gives us

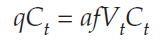
    clipboard_ec8396f421e7a939a05387f3a97f9a0ad.png

    Dividing both sides by Ct, we get

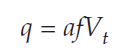
    clipboard_e546ed1c97ea231491d936328bd9d3330.png

     

     

    Dividing both sides by af gives us our solution:

    clipboard_efb0cf733eafc46a0e5793d2005198a6b.png

    In words, the predator population reaches equilibrium when the prey population equals the predator’s starvation rate over the product of attack rate times conversion efficiency.  Note that this is also a constant, and like the solution for the prey population, it does not specify the equilibrium size of the predator population, only the size of the prey population at which the predators are at equilibrium. 

     

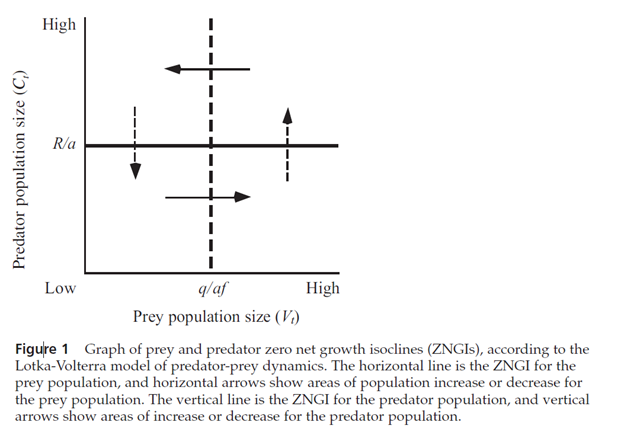
    As we did in the model of interspecific competition, we can plot the population sizes of the two interacting populations on the two axes of a graph (Figure 1). The equilibrium solutions (Equations 3 and 4) then become straight-line zero net growth isoclines (ZNGIs), as they did in the interspecific competition model.

    On this graph, the ZNGI for the prey population is a horizontal line at Ct = R/a (the solid line in Figure 1), below which the prey population increases, and above which it decreases (solid arrows).

    The ZNGI for the predator population is a vertical line at Vt = q/af (dashed line), to the left of which the predator population decreases, and to the right of which it increases (dashed arrows).

    Where the two lines cross, the two populations are at equilibrium. As in the Interspecific Competition exercise, the two populations are represented by a point on this phase diagram, and that point will trace out a trajectory through phase space as the populations change in size.

    As discussed in most ecology texts, the continuous-time Lotka-Volterra model predicts that the point representing the two populations will cycle endlessly around the point where the two ZNGIs cross.

     

    clipboard_e82fbdccdd2b2e193f4920ed1f1eaf573.png

     

    LITERATURE CITED

    King, A. A. and W. M. Schaffer. 2001. The geometry of a population cycle: A mechanistic model of snowshoe hare demography. Ecology 82: 814–830.

    Rosenzweig, M. L. and R. H. MacArthur. 1963. Graphical representation and stability conditions of predator-prey interactions. American Naturalist 97: 209–223.

     

     

    ES 211 – Lokta-Volterra Terms Sheet

    The terms we will use in ES 211 are slightly different than those above. The equations in the terms sheet below are the same as the equations shown above for ΔC (“consumer”, in our sheet, dNpred/dt) and ΔV (“victim”, in our sheet dNprey/dt)

     

    clipboard_e13e41e4a3f8dd62438c7d5f9e054b62e.png

    clipboard_ec8624a7a028de647d21e7219f3d441e2.png

     

    dNprey/dt = rate of change in prey population (change in number over change in time)

    dNpred/dt = rate of change in predator population (change in number over change in time)

    c = rate at which prey are converted into offspring (a slope: predators produced per predator per time as a function of prey consumed per unit time)

    p = attack rate efficiency (a slope: the change in prey consumed per predator per time as a function of the number of prey); higher search or handling time leads to a lower p

    dpred = predator death rate

    rprey = prey per capita rate of increase

    Nprey = number of prey

    Npred = number of predators

    Isocline of Zero Growth for Prey occurs at Npred = rprey/p 

    Isocline of Zero Growth for Predator occurs at Nprey = d/cp

    10.2: Modelling Predator-Prey Interactions is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
    2. Tags
      This page has no tags.