4.1: Population Demographics and Dynamics

Imagine sailing down a river in a small motorboat on a weekend afternoon; the water is smooth, and you are enjoying the sunshine and cool breeze when suddenly you are hit in the head by a 20-pound silver carp. This is a risk now on many rivers and canal systems in Illinois and Missouri because of the presence of Asian carp. This fish—actually a group of species including the silver, black, grass, and big head carp—has been farmed and eaten in China for over 1,000 years. It is one of the most important aquaculture food resources worldwide. In the United States, however, Asian carp is considered a dangerous invasive species that disrupts ecological community structure to the point of threatening native species. The effects of invasive species (such as the Asian carp, kudzu vine, predatory snakehead fish, and zebra mussel) are just one aspect of what ecologists study to understand how populations interact within ecological communities, and what impact natural and human-induced disturbances have on the characteristics of communities.

Populations are dynamic entities. Their size and composition fluctuate in response to numerous factors, including seasonal and yearly changes in the environment, natural disasters such as forest fires and volcanic eruptions, and competition for resources between and within species. The study of populations is called demography.

Population Size and Density

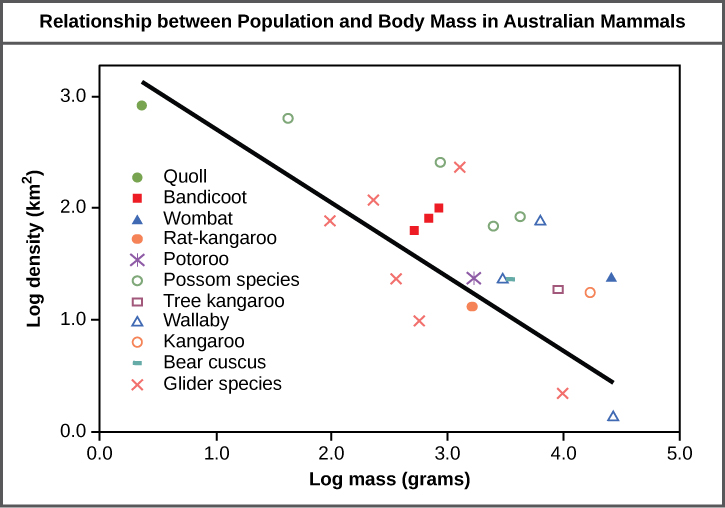
Populations are characterized by their population size (total number of individuals) and their population density (number of individuals per unit area). A population may have a large number of individuals that are distributed densely, or sparsely. There are also populations with small numbers of individuals that may be dense or very sparsely distributed in a local area. Population size can affect potential for adaptation because it affects the amount of genetic variation present in the population. Density can have effects on interactions within a population such as competition for food and the ability of individuals to find a mate. Smaller organisms tend to be more densely distributed than larger organisms (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\). Australian mammals show a typical inverse relationship between population density and body size. As this graph shows, population density typically decreases with increasing body size. Why do you think this is the case?

Estimating Population Size

The most accurate way to determine population size is to count all of the individuals within the area. However, this method is usually not logistically or economically feasible, especially when studying large areas. Thus, scientists usually study populations by sampling a representative portion of each habitat and use this sample to make inferences about the population as a whole. The methods used to sample populations to determine their size and density are typically tailored to the characteristics of the organism being studied. For immobile organisms such as plants, or for very small and slow-moving organisms, a quadrat may be used. A quadrat is a square structure that is randomly located on the ground and used to count the number of individuals that lie within its boundaries. To obtain an accurate count using this method, the square must be placed at random locations within the habitat enough times to produce an accurate estimate.

For smaller mobile organisms, such as mammals, a technique called mark and recapture is often used. This method involves marking captured animals in and releasing them back into the environment to mix with the rest of the population. Later, a new sample is captured and scientists determine how many of the marked animals are in the new sample. This method assumes that the larger the population, the lower the percentage of marked organisms that will be recaptured since they will have mixed with more unmarked individuals. For example, if 80 field mice are captured, marked, and released into the forest, then a second trapping 100 field mice are captured and 20 of them are marked, the population size (N) can be determined using the following equation:

\[N = \frac{(\text{number marked first catch} \times \text{total number of second catch})}{\text{number marked second catch}}\]

Using our example, the equation would be:

\[\frac{(80 \times 100)}{20} = 400\]

These results give us an estimate of 400 total individuals in the original population. The true number usually will be a bit different from this because of chance errors and possible bias caused by the sampling methods.

Species Distribution

In addition to measuring size and density, further information about a population can be obtained by looking at the distribution of the individuals throughout their range. A species distribution pattern is the distribution of individuals within a habitat at a particular point in time—broad categories of patterns are used to describe them.

Individuals within a population can be distributed at random, in groups, or equally spaced apart (more or less). These are known as random, clumped, and uniform distribution patterns, respectively (Figure \(\PageIndex{2}\)). Different distributions reflect important aspects of the biology of the species. They also affect the mathematical methods required to estimate population sizes. An example of random distribution occurs with dandelion and other plants that have wind-dispersed seeds that germinate wherever they happen to fall in favorable environments. A clumped distribution, may be seen in plants that drop their seeds straight to the ground, such as oak trees; it can also be seen in animals that live in social groups (schools of fish or herds of elephants). Uniform distribution is observed in plants that secrete substances inhibiting the growth of nearby individuals (such as the release of toxic chemicals by sage plants). It is also seen in territorial animal species, such as penguins that maintain a defined territory for nesting. The territorial defensive behaviors of each individual create a regular pattern of distribution of similar-sized territories and individuals within those territories. Thus, the distribution of the individuals within a population provides more information about how they interact with each other than does a simple density measurement. Just as lower density species might have more difficulty finding a mate, solitary species with a random distribution might have a similar difficulty when compared to social species clumped together in groups.

Figure \(\PageIndex{2}\). Species may have a random, clumped, or uniform distribution. Plants such as (a) dandelions with wind-dispersed seeds tend to be randomly distributed. Animals such as (b) elephants that travel in groups exhibit a clumped distribution. Territorial birds such as (c) penguins tend to have a uniform distribution. (credit a: modification of work by Rosendahl; credit b: modification of work by Rebecca Wood; credit c: modification of work by Ben Tubby)

Life tables provide important information about the life history of an organism and the life expectancy of individuals at each age. They are modeled after actuarial tables used by the insurance industry for estimating human life expectancy. Life tables may include the probability of each age group dying before their next birthday, the percentage of surviving individuals dying at a particular age interval (their mortality rate, and their life expectancy at each interval. An example of a life table is shown in Table 1 from a study of Dall mountain sheep, a species native to northwestern North America. Notice that the population is divided into age intervals (column A).

As can be seen from the mortality rate data (column D), a high death rate occurred when the sheep were between six months and a year old, and then increased even more from 8 to 12 years old, after which there were few survivors. The data indicate that if a sheep in this population were to survive to age one, it could be expected to live another 7.7 years on average, as shown by the life-expectancy numbers in column E.

Table 1: Life Table of Dall Mountain Sheep

Age interval (years)	Number dying in age interval out of 1000 born	Number surviving at beginning of age interval out of 1000 born	Mortality rate per 1000 alive at beginning of age interval	Life expectancy or mean lifetime remaining to those attaining age interval
0–0.5	54	1000	54.0	7.06
0.5–1	145	946	153.3	—
1–2	12	801	15.0	7.7
2–3	13	789	16.5	6.8
3–4	12	776	15.5	5.9
4–5	30	764	39.3	5.0
5–6	46	734	62.7	4.2
6–7	48	688	69.8	3.4
7–8	69	640	107.8	2.6
8–9	132	571	231.2	1.9
9–10	187	439	426.0	1.3
10–11	156	252	619.0	0.9
11–12	90	96	937.5	0.6
12–13	3	6	500.0	1.2
13–14	3	3	1000	0.7

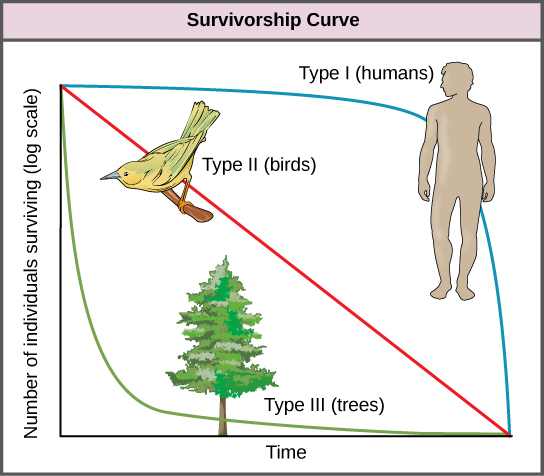
Another tool used by population ecologists is a survivorship curve, which is a graph of the number of individuals surviving at each age interval versus time. These curves allow us to compare the life histories of different populations (Figure \(\PageIndex{3}\)). There are three types of survivorship curves. In a type I curve, mortality is low in the early and middle years and occurs mostly in older individuals. Organisms exhibiting a type I survivorship typically produce few offspring and provide good care to the offspring increasing the likelihood of their survival. Humans and most mammals exhibit a type I survivorship curve. In type II curves, mortality is relatively constant throughout the entire life span, and mortality is equally likely to occur at any point in the life span. Many bird populations provide examples of an intermediate or type II survivorship curve. In type III survivorship curves, early ages experience the highest mortality with much lower mortality rates for organisms that make it to advanced years. Type III organisms typically produce large numbers of offspring, but provide very little or no care for them. Trees and marine invertebrates exhibit a type III survivorship curve because very few of these organisms survive their younger years, but those that do make it to an old age are more likely to survive for a relatively long period of time.

Figure \(\PageIndex{3}\). Survivorship curves show the distribution of individuals in a population according to age. Humans and most mammals have a Type I survivorship curve, because death primarily occurs in the older years. Birds have a Type II survivorship curve, as death at any age is equally probable. Trees have a Type III survivorship curve because very few survive the younger years, but after a certain age, individuals are much more likely to survive.

Contributors and Attributions

• Population Demography by OpenStax is licensed under CC BY 4.0. Modified from the original by Matthew R. Fisher.