24.3: Computational Techniques

This section will focus on techniques on processing raw data from the ENCODE project. Before ENCODE data can be analyzed (e.g. for motif discovery, co-association analysis, signal aggregation over elements, etc), the raw data must be processed.

Even before the data is processed, some quality control is applied. Quality control is needed for several reasons. Even without anti-bodies, reads are not uniformly-scattered. The biological reasons include non- uniform fragmentation of the genome, open chromatin regions fragmenting easier, and repetitive sequences over-collapsed in assembled genomes. The ENCODE project corrected for these biases in several ways. Portions of the DNA were removed before the ChIP step, removing large portions of unwanted data. Control experiments were also conducted without the use of anti-bodies. Finally, fragment input DNA sequence reads were used as a background.

Because of inherent noise in the ChIP-seq process, some reads will be of lower quality. Using a read quality metric, reads below a threshold were thrown out.

Shorter reads (and to a lesser extent, longer reads) can map to exactly one location (uniquely mapping), multiple locations (repetitive mapping), or no locations at all (unmappable) in the genome. There are many potential ways to deal with repetitive mapping, ranging from probabilistically spreading the read to use an EM approach. However, since the ENCODE project aims to be as correct as possible, it does not assign repetitive reads to any location.

Figure 24.3: ENCODE uniform Processing Pipeline

ENCODE Project. All rights reserved. This content is exculeded from our Creative

Commons license. For more information, see http://ocw.mit.edu/help/faq-fair-use/.

If a sample does not contain sucient DNA and/or if it is over-sequenced, you will simply be repeatedly sequencing PCR duplicates of a restricted pool of distinct DNA fragments. This is known a low-complexity library and is not desirable. To solve this problem, a histogram with the number of duplicates is created and samples with a low non-redundant fraction (NRF) are thrown out.

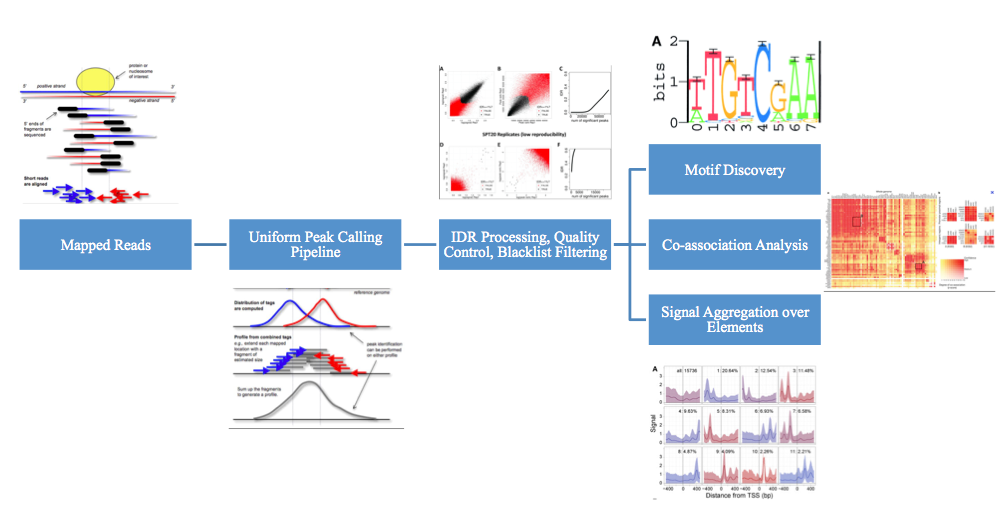
ChIP-seq randomly sequences from one end of each fragment, so to determine which reads came from which segment, typically strand cross-correlation analysis is used [Fig. 04]. To accomplish this, the forward and and reverse strand signals are calculated. Then, they are sequentially shifted towards each other. At every step, the correlation is calculated. At the fragment length offset f, the correlation peaks. f is the length at which ChIP DNA is fragmented. Using further analysis, we can determine that we should have a high absolute cross-correlation at fragment length, and high fragment length cross-correlation relative to read-length cross-correlation. The RSC (Relative Strand Correlation) should be greater than 1.

Figure 24.4: Shifting forward and reverse strand signals, Cross Correlation plot

\[R S C=\frac{C C_{\text {fragment}}-\min (C C)}{C C_{\text {readlength}}-\min (C C)}\]
Once quality control is applied, the data is further processed to determine actual areas of enrichment. To accomplish this, the ENCODE project used a modified version of peak calling. There are many existing peak calling algorithms, but the ENCODE project used MACS and PeakSeq, as they are deterministic. However, it is not possible to set a uniform p-value or false discovery rate (FDR) constant. The FDR and p-value depends on ChIP and input sequencing depth, the binding ubiquity of the factor, and is highly unstable. Moreover, different tools require different values.

The ENCODE project uses replicates (of the same experiment) and combines the data to find more meaningful results. Simple solutions have major issues: taking the union of the peaks keeps garbage from both, the intersection is too stringent and throws away good peaks, and taking the sum of the data does not exploit the independence of the datasets. Instead, the ENCODE project uses the independent discovery rate (IDR). The key idea is that true peaks will be highly ranked in both replicates. Thus, to find significant peaks, the peaks are considered in rank order, until ranks are no longer correlated.

Figure 24.5: IDR to assess reproducibility of CHIP-seq datasets. Scatter plots display signal scores of peaks that overlap in each replicate pair. (A,B) results for high quality replicate. (C) Estimated IDR for varying rank thresholds. [1]

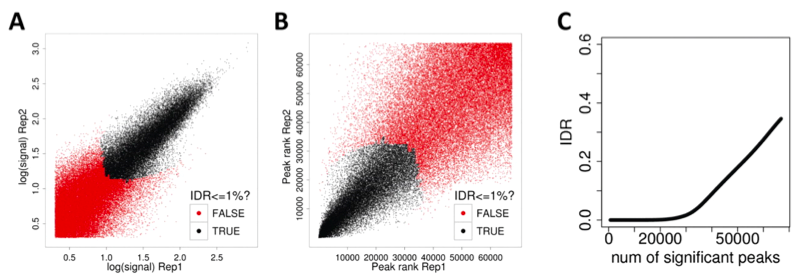
The cutoff could be different for the two replicates and actual peaks included may differ between replicates. It is modeled as a Gaussian mixture model, which can be fit via an EM-like algorithm. Using IDR leads to higher consistence between peak callers. This is because FDR only relies on enrichment over input, IDR exploits replicates. Also, using sampling methods, if there is only one replicate, the IDR pipeline can still be used with pseudo-replicates.