14.5: Reconstruction
- Page ID
- 40999
Reconstruction of reads is a largely statistical problem. The goal is to determine a score for each fixed-sized window in the genome. This score represents the probability of seeing the observed number of reads given the window size. In other words, is the number of reads in a particular window unlikely given the genome? The expected number of reads per window is derived from a uniform distribution based on the total number of reads (Figure 3). This score is modeled by a Poisson distribution.
However, this score must account for the problem of multiple testing hypotheses, due to the approximately 150 million expected bases. One option for dealing with this is the Bonferroni correction, where the nominal
Figure 14.3: Box 1: How Do We Calculate qMS?


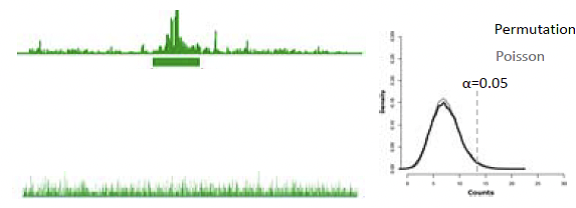
Figure 14.4: Figure 3: Reconstruction works by determining, for a particular window, the probability of observing that number of reads (top left) given the uniform distribution of the total reads (bottom left). This probability follows the Poisson distribution.
p-value = n * p-value. This method leads to low sensitivity, due to its very conservative nature. Another option is to permute the reads observed in the genome, and find the maximum number of reads seen on a single base. This allows for a max count distribution model, but the process is very slow. The scan distribution speeds up this process by computing a closed form for max count distribution to account for dependency of overlapping windows (Figure 4). The probability of observing k reads on a window of size w in a genome of size L given a total of N reads can be approximated by [slide is not clear].
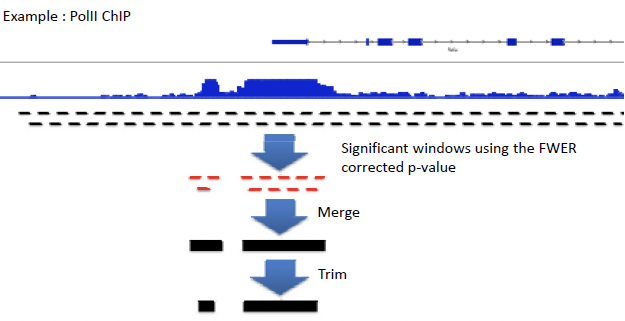
Figure 14.5: Figure 4: Process for reconstructing genome based on reads, using the scan distribution
Choosing a window size is also an important decision, as genes exist at different expression levels and span different orders of magnitude. Small windows are better at detecting punctuate regions, while larger windows can detect longer spans of moderate enhancement. In most cases, windows of different sizes are used to pick up signals of varying size.
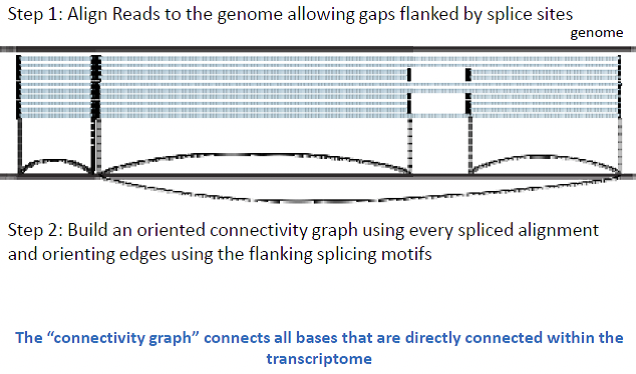
Transcript reconstruction can be seen as a segmentation problem, with several challenges. As mentioned above, genes are expressed at different levels, over several orders of magnitude. In addition, the reads used for reconstruction are obtained from both mature and immature mRNA, the latter still containing introns. Finally, many genes have multiple isoforms, and the short nature of reads makes it difficult to differentiate between these different transcripts. A computational tool called Scripture uses a priori knowledge of fragment connectivity to detect transcripts.
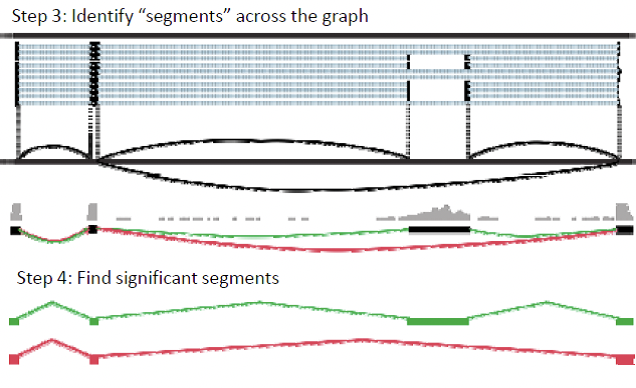
Alternative isoforms can only be detected via exon junction spanning reads, which contain the ends of an exon. Longer reads have a greater chance of spanning these junctions (Figure 5). Scripture works by modeling the reads using graph structure, where bases are connected to neighbor bases, as well as splice neighbors. This process differs from the string graph technique, because it focuses on whole genome, and does not map overlapping sequences directly. When sliding the window, Scripture can jump across splice junctions yet still examine alternative isoforms. From this oriented connectivity graph, the program identifies segments across the graph, and looks for significant segments (Box 2).
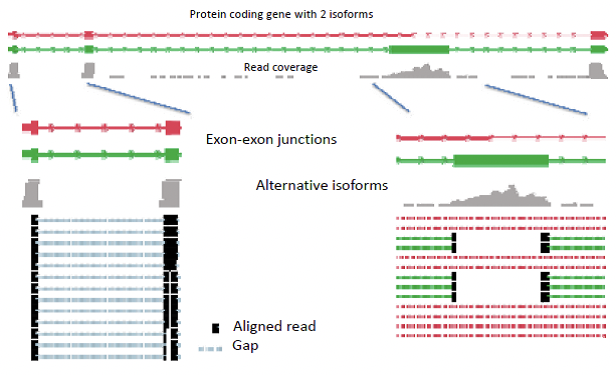
Figure 14.6: Figure 5: Alternative isoforms present a challenge for reconstruction, which must depend on exon junction spanning reads
Direct transcript assembly is another method of reconstruction (as opposed to genome-guided methods like Scripture). Transcript assembly methods are able to reconstruct transcripts from organisms without a reference sequence, while genome-guided approaches are ideal for annotating high quality genomes and expanding the catalog of expressed transcripts. Hybrid approaches are used for lesser quality transcripts or transcriptomes that have underwent major rearrangements, such as those of cancer cells. Popular transcript assembly tools include Oasis, Trans-ABySS, and Trinity. Another popular genome-guided software is Cufflinks. Regardless of methodology or software type, any sequencing experiment that produces more genome coverage will experience better transcript reconstruction.
Figure 14.7: Box 2: The Scripture Method