4.3: Deriving Simple Energy Relationships
- Page ID
- 16431
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A. Energy in the Universe: the Universe is a Closed System
Consider an event, any even. I think we can agree that when stuff happens, participants in the happening go from an unstable state to a relatively more stable state. For example, you carrying a bag of marbles and you accidentally drop the bag. The marbles would fall to the floor, roll and spread out, eventually coming to a stop. At that point, the marbles are in a more stable state than they were when you were holding the bag.
If asked, you would say that gravity made the marbles fall from the bag. That is certainly true. Could we then say that the drive to greater stability is what made the marbles fall? In fact, regardless of the force or impetus for the event, we can say that the drive to achieve greater stability that makes things/events happen! This is the essence of the Second Law of Thermodynamics: all universal energy transfer events occur with an increase in stability…, that is, an increase in entropy. We’ll consider the second law and entropy in detail shortly.
The tendency of things go from unstable to more stable is a natural, rational state of affairs…, like those marbles on the floor, or a messy bedroom with clothes strewn about. Intuitively, messy and disordered is more stable than ordered. Of course, marbles dropping or clothing going from folded and hung to wrinkled on the floor releases energy (potential energy) as they fall (kinetic energy). If you don’t believe that this release of energy is real, just think of how much energy you will need to pick up the marbles or re-fold your clothes (after laundering them of course!).
We can model the flow of energy in the universe in a way that is consistent with thermodynamic laws. Since the First law of Thermodynamics says that energy can be neither created nor destroyed, a simple statement of the First Law could be:
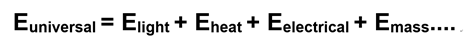
The equation sums up the different kinds of energy in the universe. Look at it this way:
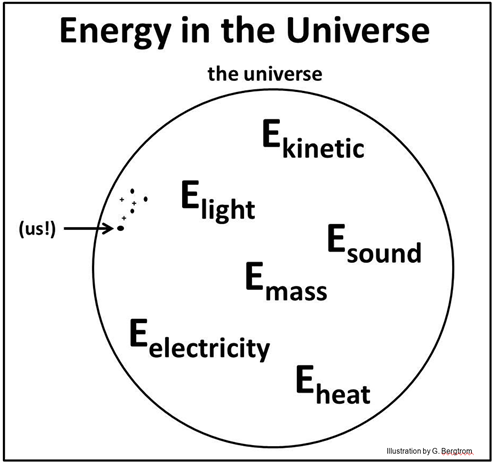
Energy cannot get in or out of the universe. Energy can only be transferred from one place to another, or converted from one form to another. It follows then that Euniversal is the sum of all kinds of energy in the universe, and that this sum is a constant. The equation below is consistent with this idea.
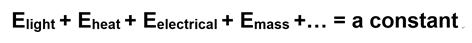
This is a statement of the First Law of Thermodynamics.
139 First Law of Thermodynamics
If we go with the simpler binary notion or useful and useless energy, our equation shortens to the sum of just two kinds of energy in the universe:

In this equation, G is useful energy (“Gibbs” free energy ), S is useless energy (entropy), and T is absolute temperature (included because of the third law). This is also a statement of the First Law. Here is our revised circle diagram:

By the way, segregating things and concepts into circles is a way of logically viewing relationships between them. John Venn first formalized this approach in the late 19th century. The Venn diagrams used here to describe the universe are very simple. For examples of more complex overlapping components of the universe that share some but not all attributes, “Google” Venn Diagrams.
In this binary energy model, it follows that as universal entropy increases, free energy in the universe must decrease:
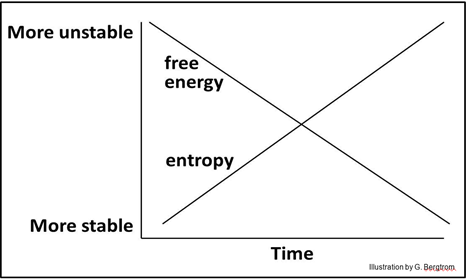
Free or ‘potentially useful’ energy is higher in more ordered, complex and therefore relatively unstable systems. Such unstable, ordered systems will release free energy spontaneously.
While the arithmetic statements about changes in energy are useful concepts, the parameters are of course, not measurable! But if we isolate a bit of the universe, we can measure energies and watch energy flow.
B. Energy is Exchanged Between Systems in the Universe
If we can measure the amount of energy put into or removed from a system within the universe, we can write a more useful equation to follow the transfer of energy between a system and its surroundings:
\[ΔH = ΔG + TΔS\]
In this formula, \(ΔH\) is the change (D) in enthalpy, i.e., as energy entering/leaving the system in units of heat energy); \(ΔG\) is change in free energy and \(ΔS\) is change in entropy; T = absolute temperature (oK).
Heat given off in a reaction (or other event) is often confused with entropy. It is true that much of the increase in entropy that occurs in living things is indeed in the form of random molecular motion, or heat. But remember that heat can have its uses; not all heat is entropic! Hence, it is more interesting (and accurate!) to think of energy in terms of changes in enthalpy, free energy and entropy during energy transfers.
According to the equation \(ΔH = ΔG + TΔS\), interacting systems in our universe would seem to be closed systems. Accordingly, energy put into or removed from the system (\(ΔH\)) will be exactly balanced by increases and/or decreases in the other two terms in the equation (\(ΔG + TΔS\)). Recall that we refer to these systems as closed systems not because they are really closed, but because we can isolate them well enough to account for energy flow into and out of the system. The value of this (or any) algebraic equation with three variables is that if you know two of the values, you can calculate the third! Here is a simple situation to illustrate the point: If I put a liter of water on a burner and light the flame, the water gets hot. If the temperature of the liter of water rises by 1oC, we know that it has absorbed 1000 calories (one Kcal, or one food Calorie) of the heat from the burner.
Since energy interactions depend on different physical conditions, such as temperature and air pressure, we need to standardize those conditions when conducting experiments that measure energy changes in experimentally isolated systems. For more on how standardizing these physical parameters enables measuring energy change in chemical reactions (in fact, any energy exchange), click the link below.
141 Deriving Closed System Thermodynamics
Turning to bioenergetics, let’s apply the equation \(ΔH = ΔG + TΔS\) to chemical reactions in cells. Because most life on earth lives at sea level where the air pressure is 1 atmosphere and the temperature is in the 20’s (Celsius), typical determinations of \(ΔH\), \(ΔG\), and \(ΔS\) are made under standard conditions where T=298oK (25oC), an atmospheric pressure of pressures of 1 atm, and a constant pH of 7.0. In addition, measured values are adjusted to calculate unimolar quantities of reactants (see below). Our equation for reactions under these standard conditions becomes: \(ΔH = ΔGo + TΔS\), where \(ΔGo\) is the standard free energy change for the reaction conducted in a closed system under standard conditions, while \(ΔH\) and \(ΔS\) are still the enthalpy and entropy changes, but determined under standard conditions.
What are unimolar conditions in practice? It means that if you burn 180 mg of glucose in a calorimeter, multiply the calories released (\(ΔH\)) by 1000. This gives you the calories released by burning 180 gm (i.e., a whole mole) of the stuff. Now we are ready to consider examples of how we determine the energetics of reactions.
c. How is Enthalpy Change (\(ΔH\)) Determined?
\(ΔH\) for a chemical reaction can easily be determined by conducting the reaction under standard conditions in a bomb calorimeter (illustrated below).

Food manufacturers determine the Calorie content of food using a bomb calorimeter. As a reaction takes place in the beaker in the illustration, it will either release or absorb heat, either heating or cooling the water in the calorimeter jacket, as measured by the thermometer. A reaction that releases heat as it reaches equilibrium is defined as exothermic, and the \(ΔH\) for an exothermic reaction will be negative. For example, a package says that a chocolate bar has 90 Calories. This means that burning the bar will generate 90 kilocalories (Kcal) of heat as measured in the calorimeter. Recall that one Calorie (with a capital C) = 1000 calories, or one Kcal. One calorie (lower case) is the energy needed to raise a gram of water by 1oC).
You are probably most familiar with reactions that release heat, but some chemical reactions actually absorb heat. Take the common hospital cold pack for example. Squeeze it to get it going and toss it in the calorimeter. You can watch the temperature in the calorimeter drop as the pack absorbs heat from the surroundings! Such reactions are defined as endothermic, with a positive \(ΔH\). OK, so we can determine the value of one of the energy parameters… we need to know at least one other, either \(ΔGo\) or \(ΔS\) before the equation \(ΔH = ΔGo + TΔS\) becomes useful.
D. How is Standard Free Energy Change (\(ΔGo\)) Determined?
As it turns out, standard free energy change, \(ΔGo\) , is directly proportional to the concentrations of reactants and products of a reaction conducted to completion (i.e., equilibrium) under standard conditions. Therefore, to determine \(ΔGo\), we need to be able to measure the concentration of reactants and reaction products before and after a chemical reaction (i.e., when the reaction reaches equilibrium). Take the following generic chemical reaction:
\[2A + B <===> 2C + D\]
The following equation relates \(ΔGo\) the equilibrium concentrations of A, B, C and D:
\[ΔGo = -RTlnKeq = -RTln((C^2+D)/(A^2+B))\]
R= the gas constant (1.806 cal/mole-deg), T = 298oK and Keq is the equilibrium constant. This is the Boltzman equation. As you can see, the Keq for the reaction is the ratio of the product of the concentrations of the products (raised to their stoichiometric powers) to the product of the concentrations of the reactants (raised to their stoichiometric powers).
If you can determine equilibrium concentrations of reactants and products in a chemical reaction, you can use this equation to calculate \(ΔGo\) (standard free energy change) for a reaction. Consider the following generic chemical reaction:
\[A + B ⇔ C + D\]
If the \(ΔGo\) is a negative number, the reaction is defined as exergonic. We say that exergonic reactions release free energy. If the \(ΔGo\) is a positive number, the reaction absorbs free energy and is defined as endergonic.
E. Working an Example Using These Equations for Closed Systems
Consider the following reaction:
\[X ⇔ Y\]
If you are given [X] and [Y], you can also do the math. At equilibrium, the concentrations of the reactants and products for this reaction measured (assayed), with the following results:
[X] = 2.5 Kcal/Mole; [Y] = 500 cal/Mole
Use the Boltzmann equation (above) to calculate the standard free energy for this reaction. What is the Keq for this reaction? What is the \(ΔGo\) for the reaction? If you did not come up with a Keq of 0.2 and an absolute value for the standard free energy for|\(ΔGo\)| of 866.2 Kcal/mole, re-calculate or collaborate with a classmate. Hint: make sure that you convert the units in your equation so that they are all the same!). Based on the calculated value of \(ΔGo\), is this reaction endergonic or exergonic?
If you conduct the reaction in a bomb calorimeter, it proceeds to equilibrium with a \(ΔH\) = -750 Kcal/Mole. What kind of reaction is this? Together with the enthalpy change, it is now possible to calculate an absolute value for the entropy change to be |\(ΔS\)| = 116.2 cal/mol-deg for this reaction. At equilibrium, did the reaction proceed with an increase or decrease in entropy under standard conditions? Again, if you did not get the correct answer, re-calculate or collaborate with a classmate.
F. Summary: The Properties of Closed Systems
First, let’s reiterate that there is no such thing as a closed system, unless of course the universe is one! What we call a closed system is simply one in which we can measure the energy going into or coming out of the system, and within which we can measure energy transfers and transductions (changes from one kind of energy to another.
Features of systems can be defined by their properties:
Properties of Closed Systems
- Closed systems are experimentally defined by an investigator.
- Standard conditions apply.
- Energy entering or leaving the system is measurable.
- Reactions reach equilibrium regardless of reaction rate.
- Product and reactant concentrations at equilibrium are constant.
- Measured energy transfer/transduction values are constant.
G. Actual Free Energy Change in Open Systems
Later we will be discussing the flow of energy through living things, from sunlight to chemical energy in nutrient molecules into ATP, from chemical energy as ATP into the performance of all manner of cellular work. Cells are open systems that constantly exchange mass and energy with their environment and never reach equilibrium. In addition, diverse organisms live under very different atmospheric conditions and maintain different body temperatures (e.g., your cat has a higher body temperature than you do!). Clearly, the conditions under which cells conduct their biochemical reactions are decidedly non-standard. However, while open systems do not reach equilibrium, they do achieve a steady state in which the rate of input of energy and matter is equal to the rate of output of energy and matter. Think of a biochemical pathway like glycolysis. If a cell’s energy needs are constant, the pathway will reach a steady state. Of course, a cell’s need for energy (as ATP) can change as energy needs change. If it does, then the steady state of ATP production will change to meet the needs of the cell.
Since reaction rates can change (and are in fact regulated in cells), implying that the steady state of a reaction or biochemical pathway can change. We characterize open systems by their properties, as listed below.
Properties of Open Systems
- Open systems exchange energy and mass with their surroundings.
- Open systems never reach equilibrium
- They achieve steady state where the energy input rate = output rate.
- The steady state can change.
- In open systems, endergonic reactions can be energetically favorable (spontaneous).
Fortunately, there is an equation to determine free energy changes in open systems. For our chemical reaction \(2A + B <===> 2C + D\), this equation would be:
\[ΔG' = ΔGo + RT\ln(((Css)^2+Dss)/((Ass)^2+Bss))\]
Here, \(ΔG'\) is the actual free energy change for a reaction in an open system. \(ΔGo\) is the standard free energy change for the same reaction under standard conditions. In a closed system. R is again the gas constant (1.806 cal/mole-deg) and T is the absolute temperature in which the reaction is actually occurring. The subscript ‘ss’ designates reactant and product concentrations measured under steady state conditions. To determine the actual free energy of a biochemical reaction in a cell (in fact in any living tissue), all you need to know are the \(ΔGo\) for the reaction, the steady state concentrations of reaction components in the cells/tissues, and the absolute T under which the reactions are occurring.
144 The Energetics of Open Systems
Elsewhere, we will use the reactions of the glycolytic pathway to exemplify the energetics of open and closed systems. At that time, pay careful attention to the application of the terminology of energetics in describing energy flow in closed vs. open systems.


