5.2.8: Food Chains and Food Webs

Learning Objectives

• Compare and contrast betrween a food chain and a food webs
• Describe energy transfer efficiency as it relates to trophic levels

Food Chains

A food chain is a linear sequence of organisms through which nutrients and energy pass as one organism eats another. Each organism in a food chain occupies a specific trophic level (energy level), its position in the food chain. The first trophic level in the food chain is the producers. The primary consumers (the herbivores the eat producers) are the second trophic level. Next are higher-level consumers. Higher-level consumers include secondary consumers (third trophic level), which are usually carnivores that eat the primary consumers, and tertiary consumers (fourth trophic level), which are carnivores that eat other carnivores. Higher-level consumers feed on the next lower tropic levels, and so on, up to the organisms at the top of the food chain: the apex consumers. In the Lake Ontario food chain shown in Figure \(\PageIndex{1}\), the Chinook salmon is the apex consumer at the top of this food chain.

Figure \(\PageIndex{1}\): These are the trophic levels of a food chain in Lake Ontario at the United States-Canada border. Trophic levels with green algae as the primary producer,  mollusks and snails are the primary consumers, and small fish (Slimy Sculpin) are the secondary consumers. The tertiary and apex consumer is Chinook salmon.

One major factor that limits the number of steps in a food chain is energy. Much of the energy from one tropic level to the next is lost as heat, due to the second law of thermodynamics. Only about 10% of the energy transfers from one trophic level to the next trophic level. Thus, after several transfers, the amount of energy remaining in the food chain may not be great enough to support viable populations at yet a higher trophic level.

Food Webs

While food chains are simple and easy to analyze, there is a one problem when using food chains to describe most communities. Even when all organisms are grouped into appropriate trophic levels, some of these organisms can feed at more than one trophic level. In addition, species feed on and are eaten by more than one species. In other words, the linear model of trophic interactions, the food chain, is a hypothetical and overly simplistic representation of community structure. A holistic model—which includes all the interactions between different species and their complex interconnected relationships with each other and with the environment—is a more accurate and descriptive model. A food web is a concept that accounts for the multiple trophic interactions between each species (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\) This food web shows the interactions between organisms across trophic levels. Arrows point from an organism that is consumed to the organism that consumes it. All the producers and consumers eventually become nourishment for the decomposers (fungi, mold, earthworms, and bacteria in the soil). (credit "fox": modification of work by Kevin Bacher, NPS; credit "owl": modification of work by John and Karen Hollingsworth, USFWS; credit "snake": modification of work by Steve Jurvetson; credit "robin": modification of work by Alan Vernon; credit "frog": modification of work by Alessandro Catenazzi; credit "spider": modification of work by "Sanba38"/Wikimedia Commons; credit "centipede": modification of work by “Bauerph”/Wikimedia Commons; credit "squirrel": modification of work by Dawn Huczek; credit "mouse": modification of work by NIGMS, NIH; credit "sparrow": modification of work by David Friel; credit "beetle": modification of work by Scott Bauer, USDA Agricultural Research Service; credit "mushrooms": modification of work by Chris Wee; credit "mold": modification of work by Dr. Lucille Georg, CDC; credit "earthworm": modification of work by Rob Hille; credit "bacteria": modification of work by Don Stalons, CDC)

Community Productivity and Transfer Efficiency

The rate at which photosynthetic producers incorporate energy from the sun is called gross primary productivity. In a cattail marsh, plants only trap 2.2% of the energy from the sun that reaches them. Three percent of the energy is reflected, and another 94.8% is used to heat and evaporate water within and surrounding the plant. However, not all of the energy incorporated by producers is available to the other organisms in the food web because producers must also grow and reproduce, which consumes energy. At least half of the 2.2% trapped by cattail marsh plants is used to meet the plants own energy needs.

Net primary productivity is the energy that remains in the producers after accounting for the metabolic needs of the producers and heat loss. The net productivity is then available to the primary consumers at the next trophic level. One way to measure net primary productivity is to collect and weigh the plant material produced on a m² (about 10.7 ft²) of land over a given interval. One gram of plant material (e.g., stems and leaves), which is largely carbohydrate, yields about 4.25 kcal of energy when burned. Net primary productivity can range from 500 kcal/m²/yr in the desert to 15,000 kcal/m²/yr in a tropical rain forest.

In an aquatic community in Silver Springs, Florida, the gross primary productivity (total energy accumulated by the primary producers) was 20,810 kcal/m²/yr (Figure \(\PageIndex{3}\)). The net primary productivity (energy available to consumers) was only 7,632 kcal/m²/yr after accounting for energy lost as heat and energy require to meet the producer's metabolic needs.

Figure \(\PageIndex{3}\): The flow of energy through a spring ecosystem in Silver Springs, Florida. Notice that the energy decreases with each increase in trophic level. The energy content of primary producers (gross productivity) is 20,810 kcal/m²/yr. The gross productivity of primary consumers is much smaller, about 3,368 kcal/m²/yr. The gross productivity of secondary consumers is 383 kcal/m²/yr, and the gross productivity of tertiary consumers is only 21 kcal/m²/yr. The net productivity of each trophic level is less than the gross productivity because some energy is used to meet metabolic needs (respiration), and some energy is lost as heat. For example, the net productivity of primary consumers was 1,103 kcal/m²/yr, only about a third of the gross productivity.

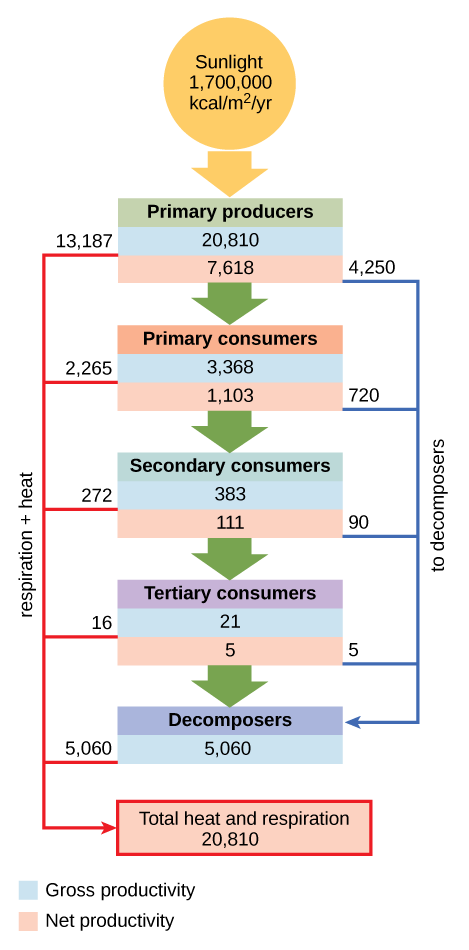
Only a fraction of the energy captured by one trophic level is assimilated into biomass, which makes it available to the next trophic level. Assimilation is the biomass of the present trophic level after accounting for the energy lost due to incomplete ingestion of food, energy used to conduct work by that trophic level, and energy lost as waste. Incomplete ingestion refers to the fact that some consumers eat only a part of their food. For example, when a lion kills an antelope, it will eat everything except the hide and bones. The lion is missing the energy-rich bone marrow inside the bone, so the lion does not make use of all the calories its prey could provide. In Silver Springs, only 1103 kcal/m²/yr from the 7618 kcal/m²/yr of energy available to primary consumers was assimilated into their biomass. (The trophic level transfer efficiency between the first two trophic levels was approximately 14.8 percent.)

Attributions

Modified by Kammy Algiers from the following sources:

2.2.1.1.4: Food Chains and Food Webs - from Biology by OpenStax (licensed CC-BY)