2.3: Using Percent Slope to Determine Tree Height
- Page ID
- 20249
2.3 Using Percent Slope to Determine Tree Height
When using percent slope to determine tree height, the tree is the rise, and the horizontal distance from the tree along the ground is the run (Figure 2.3). We can easily measure our horizontal distance from the tree, and we have instruments for measuring the percent slope to the top of a tree. So, with those two measures (run and %slope) we can solve for rise.
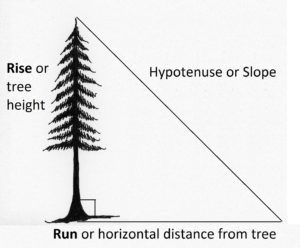
Figure 2.3. A tree makes a right angle with the ground, so a triangle or slope can be drawn using it and the ground.
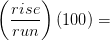 %slope
%slope
To solve the %slope equation for “rise” we do the following:
1. Multiply both sides of the equation by “run” to cancel out run on the left side of the equation
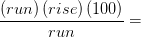 (run)(%slope)
(run)(%slope)
2. Divide both sides by “100” to cancel out 100 on the left side of the equation
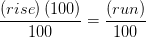 (%slope)
(%slope)
That leaves us with the following equation:
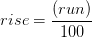 (%slope) where rise =height
(%slope) where rise =height
Notice that the %slope multiplier (100) becomes the denominator. This remains a constant. The run and %slope values are measurements, so they will change with each tree.
Here are some examples using %slope for tree height:
Example 1:
Georgia walks out a horizontal distance of 50 feet from a tree (Figure 2.4). She looks through her clinometer to determine the %slope from her eye to the top of the tree. Looking up, she reads “+124%.” Using our formula to determine the “rise:”
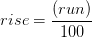 (%slope)
(%slope)
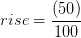 (+124) = +62 or 62 feet
(+124) = +62 or 62 feet
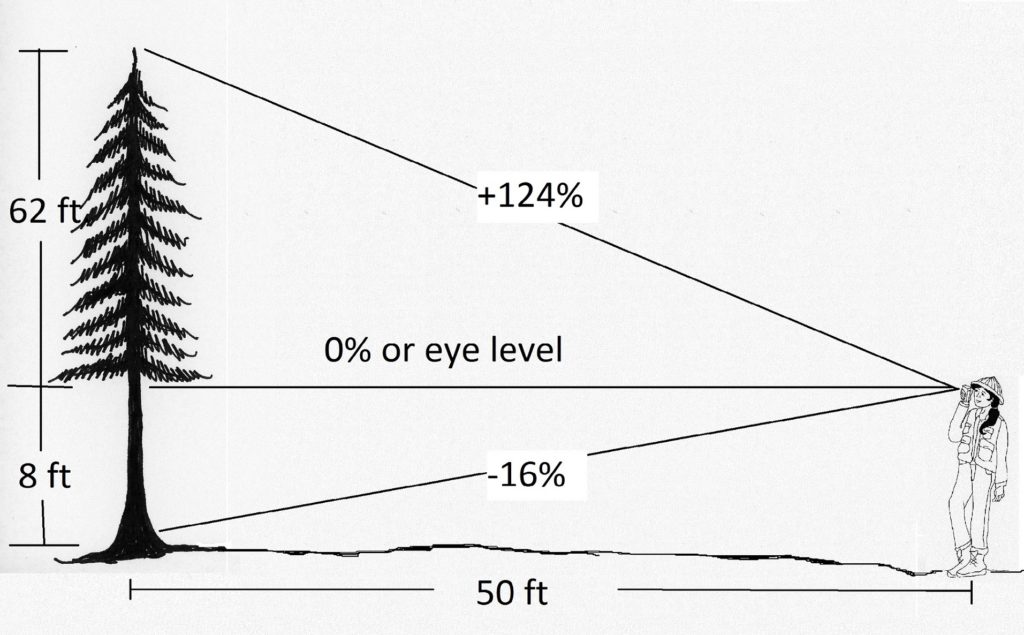
Figure 2.4. Using a clinometer and %slope to determine total tree height.
Therefore, the height of the tree from her eye to the top is 62 feet. Next, we use the same procedure to determine the height from Georgia’s eye level down to the stump. Georgia takes a reading down to the stump. She reads -16%.
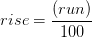 (%slope)
(%slope)
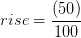 (-16) = -8 or 8 feet
(-16) = -8 or 8 feet
Georgia measured 62 feet from her eye to the top of the tree, and 8 feet from her eye to the stump of the tree. We add those two measures together to get the total height of the tree.
62 ft (top) + 8 ft (base) = 70 ft.
Remember that a negative slope measurement simply means you are looking downhill. It is important to recognize that the -8 feet is a drop in elevation, not a negative value.
We can do the two calculations in one step as follows:
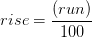 (%slope)
(%slope)
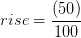 (124+16) = 70 or 70 feet
(124+16) = 70 or 70 feet
Notice Georgia put “+16” in the formula, even though the reading to the stump was a negative number. She wants to add in the bottom height, not subtract it. Again, a negative slope simply means we looked downhill. You have to think about your eye position in relation to the tree, and what the readings actually mean. Using %slope symbols algebraically can be misleading.
Example 2:
Tobias walks out a horizontal distance of 100 feet from the same tree (Figure 2.5). He looks to the top of the tree and reads “+62%” on his clinometer. He looks down to the stump and reads “-8.”
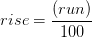 (%slope)
(%slope)
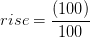 (62+8) = 70 or 70 feet
(62+8) = 70 or 70 feet
Notice that by walking farther from the tree (having a longer run), Tobias’ slope readings were smaller than Georgia’s , even though they both ended up with the same height. The angles at which Tobias was looking at the tree were smaller (less acute).
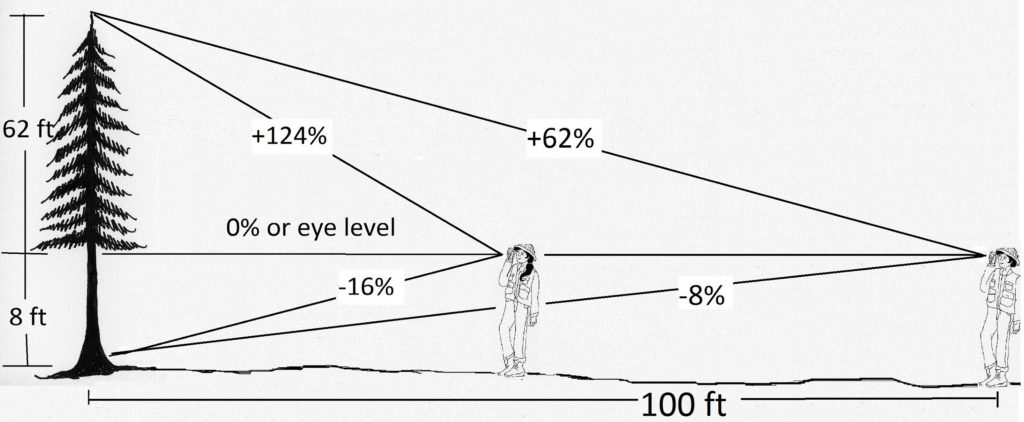
Figure 2.5. A tree can be measured from any distance, but the farther back one is from the tree, the less foreshortened the view, and generally, the more accurate the slope readings.
Also notice that when Tobias walked out 100 feet from the tree, his run equaled the denominator, 100, cancelling it out and leaving the tree equal to the readings from the clinometers. This “shortcut” makes it much easier and faster to determine tree height by reducing the number of conversions that have to be made.
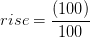 (62+8) = 70 or 70 feet
(62+8) = 70 or 70 feet
What happens at a horizontal distance of 150 feet? The slope readings are even smaller.
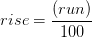 (%slope)
(%slope)
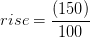 (42+5) = 70 or 70 feet
(42+5) = 70 or 70 feet
Thus, the farther one walks from the tree, the better the perspective for seeing the tree top. Being too close to the tree can result in an obscured top, as side branches will be in the way (Figure 2.6).


In the photo on the left, the tree’s top can clearly be seen. The right photo however, illustrates a foreshortened view of the top where side branches could be mistaken for the top.
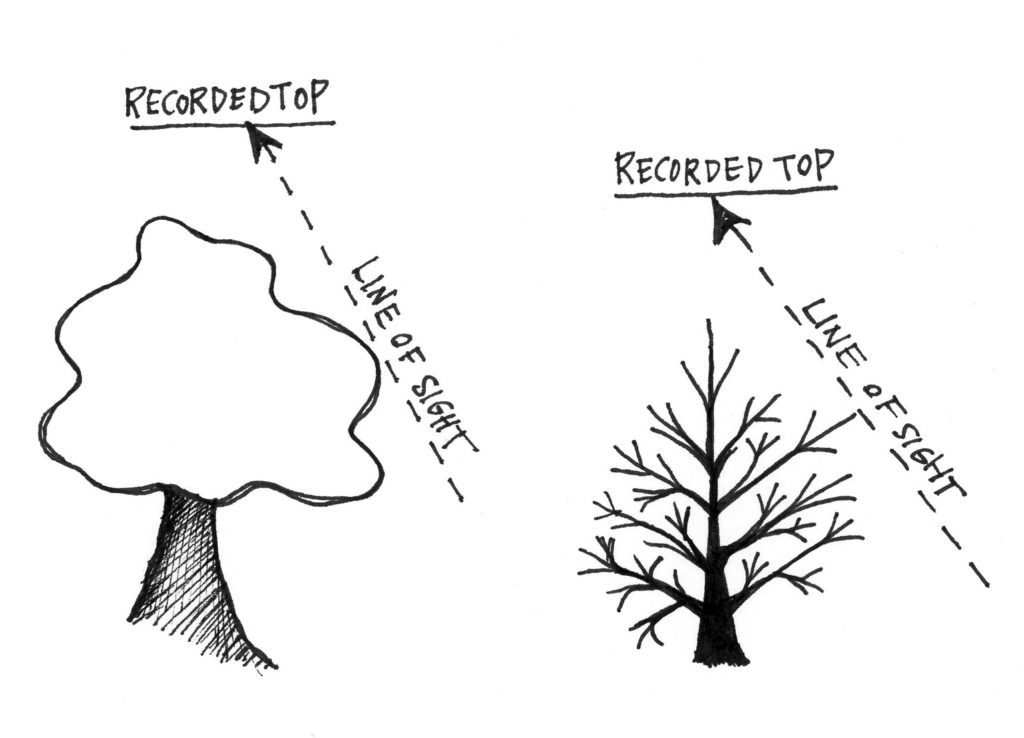
Figure 2.6. Examples of height measurement error from sighting on a side branch thought to be the top, on both a hardwood and a conifer. Height is overestimated.


