D2: Multi-Substrate Ping-Pong Mechanisms
- Page ID
- 5114
In this mechanism, one substrate binds first to the enzyme followed by product \(P\) release. Typically, product \(P\) is a fragment of the original substrate \(A\). The rest of the substrate is covalently attached to the enzyme \(E\), which is designated as \(E'\). Now the second reactant, \(B\), binds and reacts with the E' and forms a covalent bond to the fragment of \(A\) still attached to the enzyme, forming product \(Q\). This is now released and the enzyme is restored to its initial form, \(E\). This represents a ping-pong mechanism An abbreviated notation scheme is shown below for ping-pong mechanisms. For this mechanism, Lineweaver-Burk plots at varying \(A\) and different fixed values of \(B\) give a series of parallel lines.
One example of a ping-pong enzyme is low molecular weight protein tyrosine phosphatase. It reacts with the small substrate p-initrophenylphosphate (A) which binds to the enzyme covalently with the expulsion of the product P, the p-nitrophenol leaving group. Water (B) then comes in and covalently attacks the enzyme, forming an adduct with the covalently bound phosphate releasing it as inorganic phosphate. In this particular example, however, you can't vary the water concentration and it would be impossible to generate the parallel Lineweaver-Burk plots characteristic of ping-pong kinetics.
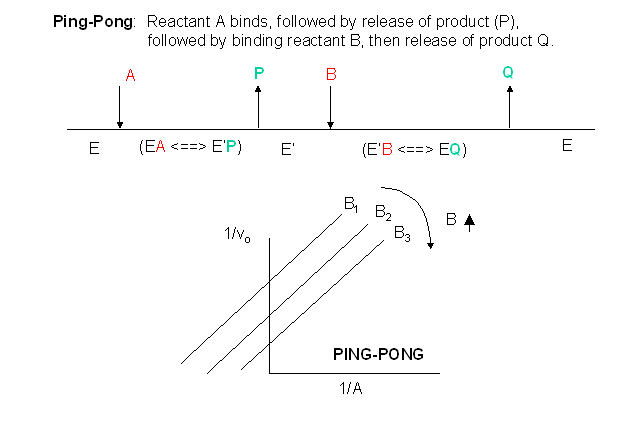
What are the meanings of the kinetic parameters, \(K_m\) and \(V_m\), for multisubstrate/multiproduct mechanisms? Consider a random sequential bi-bi reaction for a "simple" case in which the rapid equilibrium assumption defines the binding of substrates \(A\) and \(B\).

By inspection, there would appear to be two types of "effective" dissociation constants for reactant \(A\). One describes the binding of \(A\) to E (\(K_{ia}\)) and the other the binding of \(A\) to \(EB\) (\(K_a\)). Using mass balance for \(E\) and relationship that
\[v_0=k_{cat}[EAB]\]
the following initial rate equation can be derived.

Note that Kib does not appear in the final equation. How can that be? The answer lies in the fact that the final concentration of \(EAB\) can be derived from the path \(E\) to \(EA\) to \(EAB\) or from the path \(E\) to \(EB\) to \(EAB\). Assuming rapid equilibrium,
\[K_{ia}K_b=K_{ib}K_a.\]
The following equation can be derived from ping-pong bi-bi mechanism.
\[ v =\dfrac{V_M AB}{K_bA + K_aB + AB}\]
For simplicity, all of the enzyme kinetic equations have been derived assuming no products are present.


