4.10: Lineweaver-Burk Plots
- Page ID
- 3038
The study of enzyme kinetics is typically the most math intensive component of biochemistry and one of the most daunting aspects of the subject for many students. Although attempts are made to simplify the mathematical considerations, sometimes they only serve to confuse or frustrate students. Such is the case with modified enzyme plots, such a Lineweaver-Burk (Figure 4.9.1). Indeed, when presented by professors as simply another thing to memorize, who can blame students. In reality, both of these plots are aimed at simplifying the determination of parameters, such as \(K_M\) and \(V_{max}\). In making either of these modified plots, it is important to recognize that the same data is used as in making a \(V\) vs. \([S]\) plot. The data are simply manipulated to make the plotting easier.
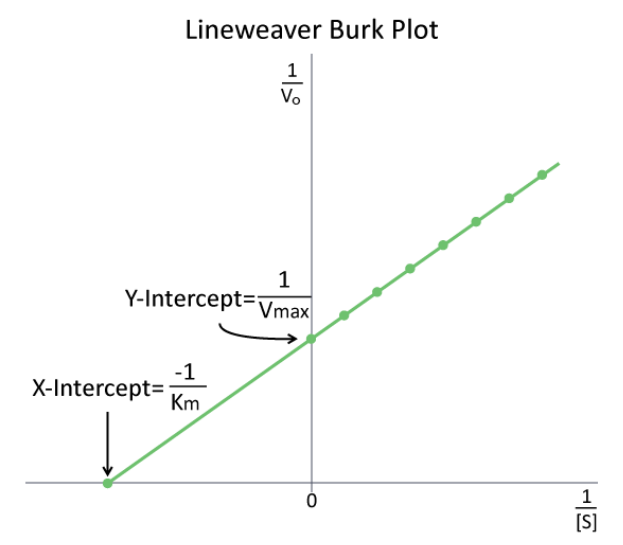
For a Lineweaver-Burk, the manipulation is using the reciprocal of the values of both the velocity and the substrate concentration. The inverted values are then plotted on a graph as \(1/V\) vs. \(1/[S\)]. Because of these inversions, Lineweaver-Burk plots are commonly referred to as ‘double-reciprocal’ plots. As can be seen at left, the value of \(K_M\) on a Lineweaver Burk plot is easily determined as the negative reciprocal of the x-intercept , whereas the \(V_{max}\) is the inverse of the y-intercept. Other related manipulation of kinetic data include Eadie-Hofstee diagrams, which plot V vs V/[S] and give \(V_{max}\) as the Y-axis intercept with the slope of the line being \(-K_M\).


