1.16: Algebra Review Guide
- Page ID
- 121699
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Linear Equations, Formulas, and Inequalities
- Eliminate denominators (multiply by Least Common Denominator)
- Remove parentheses (distribute)
- Get variable terms on one side (add/subtract principles)
- Combine like terms (for formulas, factor the variable if it appears in more than 1 term)
- Get the variable alone (multiply/divide principles)
Note: For inequalities, division or multiplication by a negative number will switch the inequality symbol around - Check the solution
An interactive H5P element has been excluded from this version of the text. You can view it online here:
https://iastate.pressbooks.pub/quantitativeplantbreeding/?p=339#h5p-79
An interactive H5P element has been excluded from this version of the text. You can view it online here:
https://iastate.pressbooks.pub/quantitativeplantbreeding/?p=339#h5p-80
An interactive H5P element has been excluded from this version of the text. You can view it online here:
https://iastate.pressbooks.pub/quantitativeplantbreeding/?p=339#h5p-81
An interactive H5P element has been excluded from this version of the text. You can view it online here:
https://iastate.pressbooks.pub/quantitativeplantbreeding/?p=339#h5p-82
An interactive H5P element has been excluded from this version of the text. You can view it online here:
https://iastate.pressbooks.pub/quantitativeplantbreeding/?p=339#h5p-83
An interactive H5P element has been excluded from this version of the text. You can view it online here:
https://iastate.pressbooks.pub/quantitativeplantbreeding/?p=339#h5p-84
An interactive H5P element has been excluded from this version of the text. You can view it online here:
https://iastate.pressbooks.pub/quantitativeplantbreeding/?p=339#h5p-85
Terminology
Various terms are used in carrying out algebraic operations. A good understanding of these enables calculations to be carried out correctly. Some common terms are shown in Table 1.
| Vocabulary | Definition |
|---|---|
| Variable | A letter that can be replaced by any number |
| Constant | A capital letter that represents a fixed number |
| Expression | Consists of variables, numbers and operation symbols (ex:  ) ) |
| Equation | When “=” is between two algebraic expressions (equation can be true 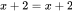 , false , false  or neither  ) ) |
| Solution | A value replacing the variable to make the equation true (  for for  ) ) |
| Solved | Having found the values that make the equation true |
| Translate | To convert words to an algebraic expression or equation |
| Substitute | Replacing a variable with a given number |
| Evaluate | To find a solution |
| Factor | Multiple or Product |
| Factoring | Reversing distributive law and turning it into the factors (multiples) |
| Equivalent | Expressions that, when evaluated, produce the same value |
| Terms | A number, var (variable), or a product/quotient of numbers and/or variables separated by + or – signs (Expression  contains three terms) contains three terms) |
| Fraction notation | A way of showing the division of two numbers (Numerator: top, Denominator: bottom) |
| Undefined | 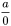 : Division by zero is undefined — There is no solution : Division by zero is undefined — There is no solution |
| Zero fraction |  : Zero in the numerator makes fraction equal to zero : Zero in the numerator makes fraction equal to zero |
| Fraction notation for 1 | Any nonzero number divided by itself is 1:  |
| Reciprocal | Multiplicative inverse: if  , ,  Zero has no reciprocals. The reciprocal of a is 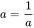 . . |
| Opposite | Additive inverse: opposite of “a” is “-a” and  . . |
| Prime number | A natural number that is divisible by only two different factors: itself and 1 |
| Inequality | A statement about the relative size of two objects. Indicated by <, >, ≪, ≫ |
| Law | Definition |
| Commutative | For any real a and b, 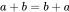 , and , and |
| Associative | For any real a, b, and c,  |
| Distributive | For any real a, b and c,  |
Operation With Fractions
Simplifying Fractions
- Prime factorize each numerator and denominator
- Remove factors that are the same from the numerator and denominator and replace them with “1”.
These form fractions that are equal to “1”. - Multiply the remaining factors in the numerator
- Multiply the remaining factors in the denominator
Simplifying Fractions Example
\[\frac{60}{126}=2^{2}\cdot 3\cdot \frac{5}{2}\cdot 3^{2}\cdot 7=\frac{10}{21}\]
Multiplying Fractions
- Prime factorize each numerator and denominator
- Remove factors that are the same from any numerator and any denominator and replace them with “1”. These form fractions that are equal to “1”.
- Multiply the remaining factors in all numerators
- Multiply the remaining factors in all denominators
Multiplying Fractions Example
\[\frac{7}{12}\cdot \frac{30}{21}=\frac{7}{2^{2}}\cdot 3\cdot 2\cdot 3\cdot \frac{5}{3}=\frac{5}{6}\]
Dividing Fractions
- Change division to multiplication by the inverse of the second fraction
- Multiply as above
Dividing Fractions Example
\[\frac{4}{18}\div\frac{10}{21}=\frac{4}{18}\cdot {\frac{21}{10}}=\frac{2^{2}}{2}\cdot 3^{2}\cdot 3\cdot \frac{7}{2}\cdot 5=\frac{1}{3}\cdot \frac{7}{5}=\frac{7}{15}\]
Add and Subtract
- If denominators are the same, go to step 4
- Otherwise, prime factorize each denominator
- Find the Least Common Denominator (LCD) by multiplying each fraction by a fraction equal to “1”, made out of the missing factors from each denominator
- Once denominators are the same, add/subtract numerators and write over the LCD
- Simplify as above
Adding/Subtracting Fractions Example 1: Same denominator
\[\frac{2}{14}+\frac{5}{14}=\frac{7}{14}=\frac{7}{2}\cdot 7=\frac{1}{2}\]
Adding/Subtracting Fractions Example 2: One denominator is a multiple of the other
\[\frac{3}{2}-\frac{5}{6}=\frac{3}{2}-\frac{5}{2}\cdot 3=\frac{3}{2}\cdot \frac{3}{3}-\frac{5}{2}\cdot 3=9-\frac{5}{2}\cdot 3=\frac{4}{2}\cdot 3=\frac{2^{2}}{2}\cdot 3=\frac{2}{3}\]
Adding/Subtracting Fractions Example 3: Different denominators
\[\frac{9}{42}-\frac{3}{15}=\frac{9}{2}\cdot 3\cdot 7-\frac{3}{3}\cdot 5=\frac{9}{2}\cdot 3\cdot 7\cdot \frac{5}{5}-\frac{3}{3}\cdot 5\cdot 2\cdot \frac{7}{2}\cdot 7=45-\frac{42}{2}\cdot 3\cdot 5\cdot 7=32\cdot 3\cdot 5\cdot 7=\frac{1}{2}\cdot 5\cdot 7=\frac{1}{70}\]
Rules of Exponents
Zero and One
Multiply and Divide
Distribute
Negative
Rules of Radicals
Add and Subtract Radicals
Simplify each radical by removing perfect square roots out of the radical to get like radicals, then combine the number of like radicals.
Multiply and Divide Radicals
\[\sqrt[n]{a}\cdot\sqrt[n]{b} =\sqrt[n]{ab}\]
\[\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\]
If no n is given, assume that n is 2, and a square root is required.
Plus/Minus Sign
Used to indicate that a value can be of either sign. Often used to construct confidence intervals.
\[p\pm x + y = p +x + y, \textrm{or p - x + y}\]
Data Transformation
Trigonometry and Natural Logarithms
| Transformation | Reciprocal of Transformation |
|---|---|
| Sine (sin) | Cosecant (csc or cosec) or Arcsine (arcsin) |
| Cosine (cos) | Secant (sec) or Arccosine (arccos) |
| Tangent (tan) | Cotangent (cot) or Arctangent (arctan) |
| Arcsine (arcsin) | Sine (sin) |
| Natural logarithm (in or log or loge) | Exponential (exp or en) |
Summation
Summation (S) signifies that a series of terms should be added together.
Given a series of numbers  ,
,  ,
, 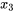 …
… 
Sum all  starting at
starting at  through
through 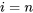 .
.
\[\sum_{i=1}^{n}x^{i}=x_{1}+x_{2}+x_{3}+x_{4} + ... + x_{n}\]
\[\textrm{Equation 1}\]
How to cite this chapter: Kendra Meade and A. A. Mahama. 2023. Algebra Review Guide. In W. P. Suza, & K. R. Lamkey (Eds.), Quantitative Methods. Iowa State University Digital Press.