Module 3.2: Charge & Buffers
- Page ID
- 24655
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)learning objective
- Calculate the net charge on a molecule, at any pH.
- Understand why solutions of weak acids resist pH changes.
- Calculate the amount of a weak acid and its conjugate base to make a buffer system.
Effect of pH on Charge of Molecules
Since protonation or deprotonation changes the charge of the ionizable group, the pH of a solution will affect the overall net charge on a molecule. The overall charge on a molecule as a function of pH can be calculated by following the following steps:
- Identify all ionizable groups on the molecule & their charge when protonated (\(q_{HA}\)) and deprotonated (\(q_{(A^-)}\)).
- Use the known \(pK_a\) of each group to determine the fraction protonated (\(f_{HA}\)) and deprotonated (\(f_{H^-}\)) at the required pH.
- Calculate the overall charge by summing the contribution of each group using the following formula.
\[q_{\text {Total}}=\sum_{i=1, n} f_{H A} q_{H A}+f_{A^-} q_{A^-}\nonumber\]
walkthrough
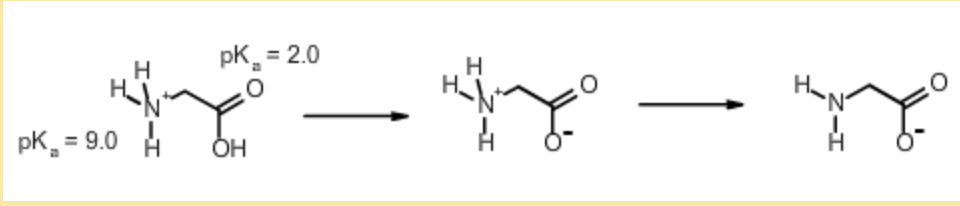
Calculate the net charge on the amino acid glycine at pH 2.0. Glycine at pH=7.0 is shown below:
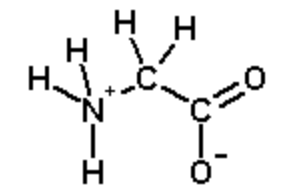
Step 1. Identify ionizable groups, their \(pK_a\) values, and their charges.
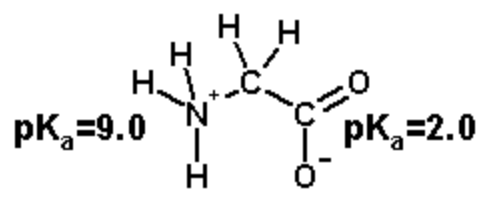
The ionizable groups are the amino and the carboxyl.
The amino group has a \(pK_a\) of 9.0 and the carboxylate has a \(pK_a\) of 2.0.
The amino group has a charge of +1 when protonated, 0 when deprotonated.
The carboxylate has a charge of 0 when protonated, -1 when deprotonated.
Step 2. Calculate the fraction protonated (\(f_{HA}\)) and deprotonated (1-\(f_{HA}\)) at the required pH.
These values can be obtained quantitatively from the formula: \(f_{HA}\)=1/(1+R), or approximated from a plot of fraction protonated versus pH:
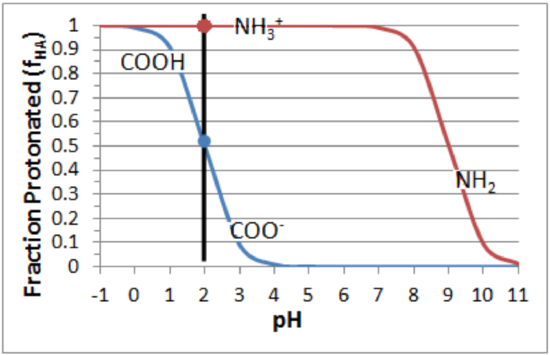
Amino group: \(pK_a\) = 9.0. At pH=2, \(f_{HA}\)=1.0, \(f_{A^-}\)=0.
Carboxyl: \(pK_a\) = 2.0. At pH=2, \(f_{HA}\)=0.5, \(f_{A^-}\)=0.5
Step 3. Calculate the overall charge by summing the contribution of each group: \(q=f_{HA}\times q_{HA}+ f_{A^-}\times q_{A^-}\)
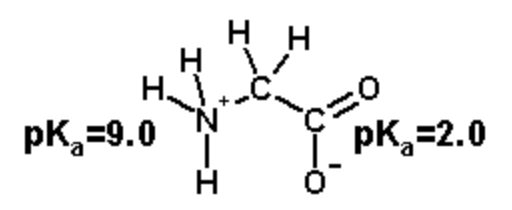
Amino group: \(q_{NH}\)=[1.0x(+1)+0.0x(0)]=+1.0
Carboxylate: \(q_{COOH}\)=[0.5x(0)+0.5x(-1)]=-0.5
Total Charge: q=+1.0 - 0.5 = +0.5
Note that this does not mean that a molecule of glycine has a charge of +0.5. Instead it means that if you average over all of the molecules in solution the charge will be +0.5. Based on the above analysis one half of the molecules will have a charge of +1 ( both groups protonated) while one half of the molecules will have a charge of 0 (amino group protonated, acid deprotonated). The net charge is the weighted average of these two populations, i.e. 0.5 = 0.5 x (+1) + 0.5 x (0.)
did i get this
1. Select the best estimate the net charge on the amino acid glycine at pH 3.0:

a. +1.0
b. +0.1
c. +0.0
d. -0.1
e. -1.0
- hint
-
There are two ionizable groups: the amino group (q=+1 when protonated, q=0 when deprotonated) and the carboxylic acid group (q=0 when protonated, q=-1 when deprotonated).
Estimate the fraction protonated and deprotonated for each group at pH=3.0. For the amino group, \(pK_a\)=9.0, therefore it will be fully protonated at pH=3.0; \(f_{HA}\)=1.0, \(f_{A^-}\)=0. For the carboxylic acid group, \(pK_a\)=2.0. At pH=3.0, \(f_{HA}\)~0.1, and \(f_{A^-}|)~0.9.
The contribution of each group to the overall charge is: q = \(q_{HA}f_{HA}+q_{A^-}f_{A^-}\)
- Answer
-
b. (the ratio of products to reactants does not change for a given substance at equilibrium.)
Measuring the \(pK_a\) --Titration Curves
\(K_a\) values, or acidity constants, must be measured by direct experiment, usually with a pH titration. Known amounts of a strong base (NaOH) are added to a solution of weak acid and the pH is measured as the amount of NaOH is added. As the base is added it removes the proton from the acid, as well as increasing the pH by removing free protons from water. A titration curve is shown below.
learn by doing
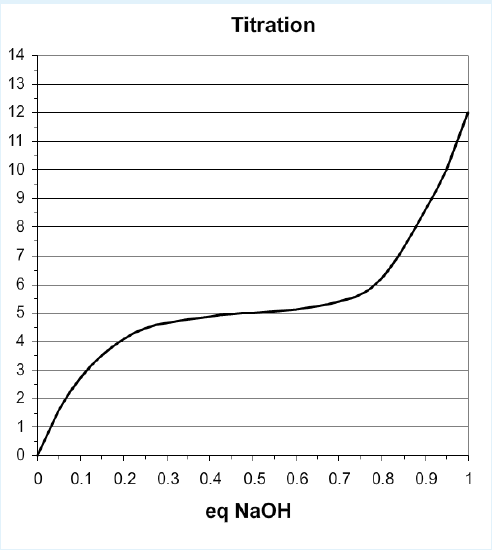
Titration Curve of Monoprotic Acid
Key features of titration curves:
- Equivalents: the x-axis scale for titrations is given in moles of base/moles of acid. Therefore, it varies from 0 to 1 for an acid that releases one proton (monoprotic), from 0 to 2 for a diprotic acid, 0 to 3 for a triprotic acid.
- Equivalence Point: Complete deprotonation of the weak acid occurs when the amount of added base is equal to, or equivalent, to the total number of ionizable protons that were originally on the weak acid. This point in the titration is referred to as the equivalence point. The equivalence point can be used to determine the concentration of the acid.
- Inflection Point (pH = \(pK_a\)): You can prove from the Henderson-Hasselbalch equation that the smallest change in pH occurs when the pH = \(pK_a\).
walkthrough
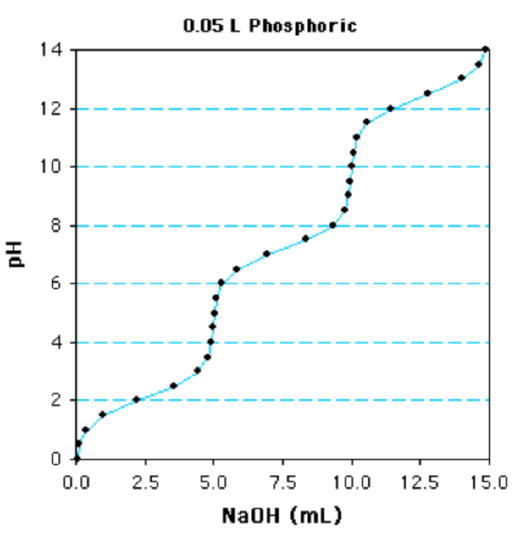
Question: The titration of a 0.05 L solution of phosphoric acid with 1 M NaOH is shown below. Is this a mono, di, or tri-protic acid? What are the individual \(pK_a\)s for each ionization? What is the concentration of the phosphoric acid?
A. Determine the nature of the Acid (monoprotic, diprotic,...).
This is a
a. monoprotoic acid because of one reflection point.
b. diprotoic acid because of two reflection points.
c. triprotoic acid because of three reflection points.
- Answer
-
c. (There are three places on the curve where there is an inflection point.)
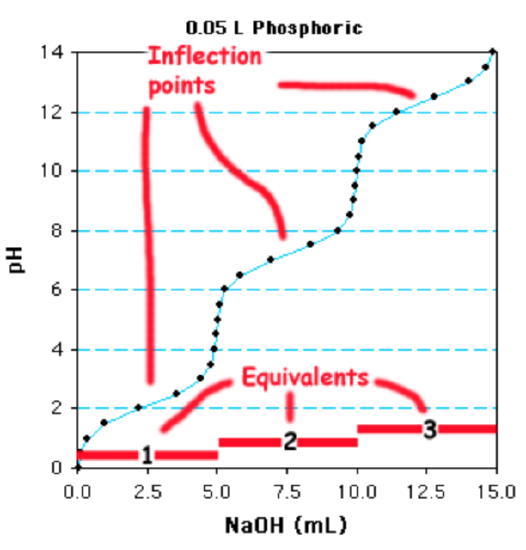
In this case there are distinct inflection points because the \(pK_a\) values are considerably different. In many cases, the individual \(pK_a\) values may be sufficiently close to each other that multiple inflection points are not clear and a steep change in pH between each ionization is no longer evident. The number of ionizable groups can still be easily determined if one of the ionizations is clearly evident. The amount of base required to titrate this group gives the volume of base to titrate one equivalent. The total volume required, divided by the volume required for one equivalent, will give the number of ionizable groups.
Using the phosphate titration as an example, the last ionization begins at 10 ml and is complete at 15 ml. Therefore 5 ml is equal to one equivalent. Since 15ml are required for the entire titration, this is a triprotic acid.
B. Determine the \(pK_a\) values.
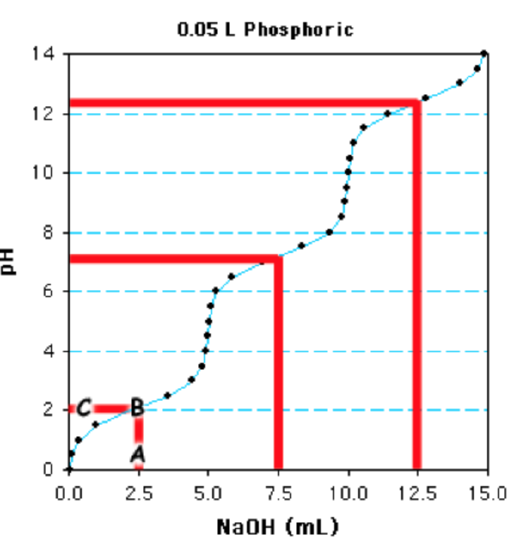
The first step is to determine the 1/2-equivalence points - at this point the pH=\(pK_a\) since the concentration of acid equals its conjugate base. This is a triprotic acid and the total volume required to titrate the acid is 15ml. Therefore 5 ml (15/3) is one equivalence and 2.5 ml will be the first 1/2 equivalence point (marked "A" on the graph). The 1/2 equivalence point for the next ionization is at 7.5ml (2.5 + 5) and the 1/2 equivalence point for the last ionization is at 12.5 ml (2.5 + 10).
The next step is to begin from the 1/2 equivalence point and move vertically on the plot until the titration curve is met (point "B"), then proceed horizontally to the y-axis ("C"). This gives the pH at the 1/2 equivalence point, ~2.2 in this case. The other two \(pK_a\) values are obtained in the same manner, beginning at 7.5 ml and 12.5 mls, giving \(pK_a\) of ~7.3 and ~12.4.
C. Determine the concentration of the acid.
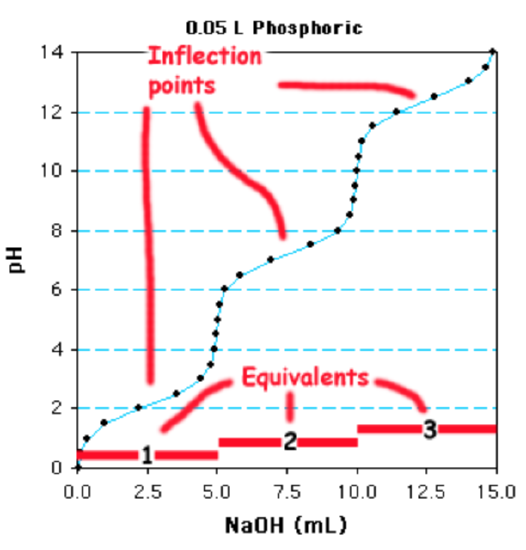
Determine the number of moles of base added: A total of 15ml of 1 M NaOH are required to fully deprotonate the acid. This is a total of 0.015 moles of base (0.015 L x 1 mole/L = 0.015 moles).
Divide by # of Ionizations to obtain the moles of weak acid:Since this is a triprotic acid, there are 0.005 moles of the weak acid (0.015/3)
Divide by the volume of the solution to obtain the molarity of the weak acid. The volume of the solution that was titrated was 0.05 L, so the concentration of the phosphoric acid is 0.005 moles/0.05L = 0.1 M, or 100 mM.
Alternatively, you can recognize that titration of a single group of the acid requires 5 ml of NaOH, which is equivalent to 0.005 moles, divide by 0.05 L = 0.1 M.
did i get this
1. The following is a titration curve for what type of acid?
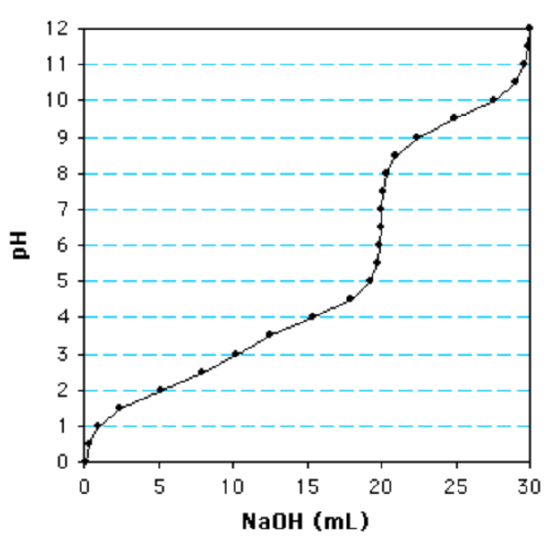
a. Monoprotic
b. Diprotic
c. Triprotic
d. None of these are true
- hint
-
Use the volume required to titrate a group to define the volume of one equivalent.
- Answer
-
c. (There is more than one inflection point. The last ionization is well separated from the others and shows that 10 ml of NaOH are required to titrate one group. Since the total volume of NaOH added is 30 ml, this is a triprotic acid.)
2. Please answer the questions at the bottom of this page using the following titration curve:
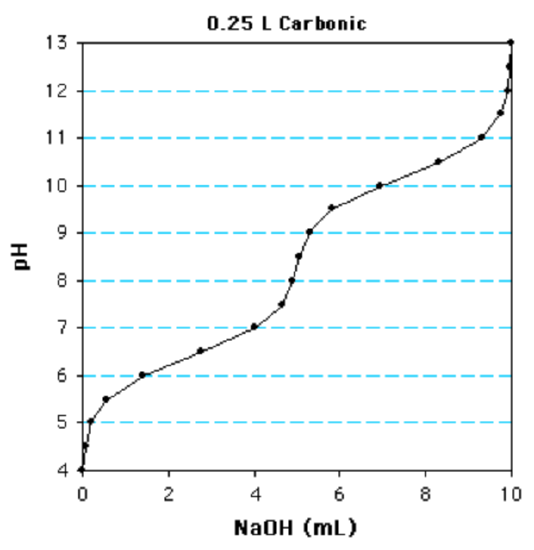
This is a monoprotic/diprotic/triprotic
- hint
-
How many inflection points, or buffer regions, are present?
The first \(pK_a\) value is 6/6.5/7/8.5/10
- hint
-
The \(pK_a\) is the pH when 1/2 equivalent has been added.
The concentration is 10mM/20mM/40mM
- hint
-
Determine the number of moles of NaOH to titrate one equivalent.
- Answer
-
diprotic (there are two buffer region); 6.5 (This is the pH when 1/2 equivalents have been added (2.5 ml)); 20 mM
Buffers
A pH buffer is an acid that resists changes in the solution pH by absorbing or releasing protons. Buffers play an important role in cellular processes because they maintain the pH at an optimal level for biological processes. They are also widely used to control pH in laboratory processes.
The buffering capacity of a solution can be understood by plotting the fraction of the weak acid that is protonated at different pH values. This plot is shown below, plotted with the same orientation as the titration curve, with the pH on the vertical axis. During the titration the fraction protonated (horizontal axis) will decrease as base is added; i.e. the curve is traced from right to left.
learn by doing
Weak Acids as Buffers
Fraction protonated as a function of pH
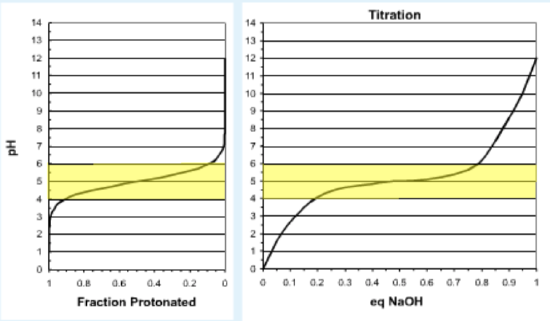
The left figure shows the fraction protonated versus pH. The right figure shows a typical titration curve, with the pH as a function of added base. The highlighted area represents the buffer region, which is given by pH=\(pK_a\) +/- 1 unit.
- At the beginning of the titration the pH is much lower than the \(pK_a\) of the acid, so the acid is fully protonated. Consequently any base that is added combines with free protons and the pH rises sharply without a significant change in the fraction protonated.
- As more base is added, the pH approaches the \(pK_a\) and the weak acid begins to ionize. The protons that are released from the acid partially neutralize the added base, thus the change in pH as base is added decreases.
- Towards the end of the titration, almost all of the weak acid is fully ionized and thus any additional base removes protons from the solution, and the pH again rises sharply.
did i get this
Which region of the curve on the right corresponds to a solution that will not resist pH changes due to the addition of a strong acid?
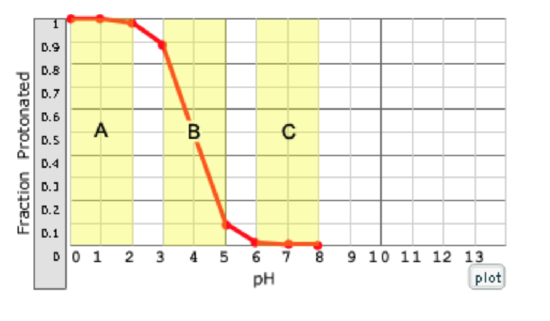
a. A
b. B
c. C
- hint
-
The ability to resist pH changes depends on the ability of the weak acid to absorb or release protons.
- Answer
-
a. (this region cannot resist changes because the weak acid is fully protonated in region A and can't accept additional protons; in region B, it can resist changes, because both HA and A are present in this region, so the weak acid can absorb additional protons; in region C, it can resist changes because the acid is fully deprotonated in region C and can absorb additional protons.)
There are two important features of buffers:
- Buffering range: This is the pH range over which the pH changes slowly when acid or base is added. The buffer range is considered to be pH values that are one unit below to one unit above the \(pK_a\). (Hi-lighted in yellow in the figure above.)
- Buffer capacity: This is the total amount of base (or acid) that can be added to a buffer solution and still have the pH with the buffer range. It depends on the concentration of the weak acid and the starting pH.
Steps in making a buffer
The goal is to make a solution of a weak acid at a defined pH. Assuming that this pH is within the buffer region of this acid (pH = \(pK_a\) +/- 1), this solution will resist, or buffer, pH changes. The Henderson-Hasselbalch equation provides some of the necessary information to make a buffer, namely the correct ratio of protonated to deprotonated weak acid to give the desired pH.
\[p H=p K_{a}+\log \frac{\left[A^{-}\right]}{[H A]}\nonumber\]
In order to obtain a solution of a weak acid at the defined pH, it is necessary to adjust the ratio of [\(A^-\)] to [HA], such that \(pK_a\)+log[\(A^-\)]/HA] equals the desired pH. The required concentrations of [\(A^-\)] and [HA] are defined by the total buffer concentration, [\(A_T\)]:
\[\begin{array}{l}{\left[A^{-}\right]=\left[A_{T}\right] f_{A^-}=\left[A_{T}\right] \frac{R}{1+R}} \\ {[H A]=\left[A_{T}\right] f_{H A}=\left[A_{T}\right] \frac{1}{1+R}}\end{array}\nonumber\]
There are three ways to obtain the indicated ratio of [HA] to [\(A^-\)]:
- Mix the indicated concentration of the acid and its conjugate base to give the desired pH.
- Use [\(A_{T}\)] amount of the acid form of the buffer and add a sufficient amount of a strong base (e.g. NaOH) to generate the required concentration of [\(A^-\)], attaining the desired pH.
- Use [\(A_{T}\)] amount of the conjugate base form of the buffer and add a sufficient amount of a strong acid (e.g. HCl) to generate the required concentration of [HA], attaining the desired pH.
In the case of the last two methods, it is usually easier to perform all of the calculations in equivalents and then determine the amount of strong base or strong acid as the number of equivalents x [\(A_{T}\)]. This approach is especially useful when polyprotic acids are used for buffers.
walkthrough
Example: Make 2L of 0.025 M buffer solution at pH 5.0 using one of the following two buffers:
Buffer \(pK_a\) MW
Histidine 6.0 155 g/mol
Pyruvate 2.5 110 g/mol
A. What buffer would you use and why?
Histidine, since its \(pK_a\) is closest to the desired pH of 5.0
B. Determine the amount of the protonated (fHA) and deprotonated (\(f_{A^-}\)) forms that would be present at pH 5.0.
i. Calculate R first, R=\(10^{(pH-pK_a)}\) = \(10^{-1}\) = 0.1
ii. Calculate \(f_{HA}\)= 1/(1+R) = (1/1.1) = 0.91
iii. Calculate \(f_{A^-}\) = R/(1+R) = (0.1/1.1) = 0.09
Now construct the buffer using one of the three methods shown on the following pages.
Method A - Mixing of (HA) and (\(A^-\))
\(f_{HA}\)= 0.91
\(f_{A^-}\) = 0.09
The total concentration of all buffer species, [\(A_T\)] is given to be 0.025 moles/L, and the total volume was 2L.
Therefore you would:
mix 0.91 x 0.025 moles/L x 2 L = 0.0455 moles of HA, or 0.0455 moles x 155 g/mol = 7.05g
mix 0.09 x 0.025 moles/L x 2 L = 0.0045 moles of \(A^-\), or 0.697g
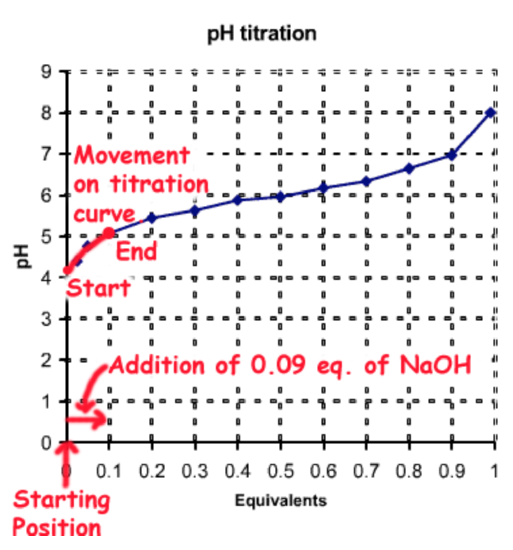
Method B - Addition of Strong Base to HA
\(f_{HA}\)= 0.91
\(f_{A^-}\) = 0.09
Beginning with one equivalent (eq.) of (HA) you would need to add 0.09 eq. of NaOH, which would deprotonate 0.09 eq. of HA to \(A^-\), generating the desired fractions of each species: \(f_{HA}\)= 0.91, \(f_{A^-}\) = 0.09.
The total number of moles of the weak acid is 0.025 moles/L x 2 L = 0.05 moles. Therefore the amount of strong base to be added is 0.05 moles x 0.09 = 0.0045 moles. This would be added to 2L of 0.025 M (HA).
This process of pH adjustment is illustrated on the following diagram:
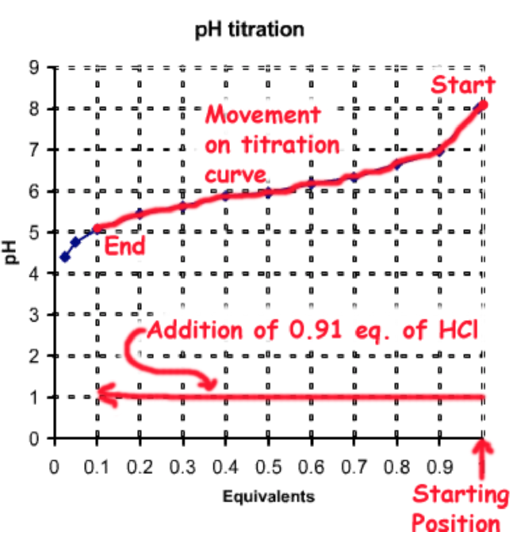
Method C - Addition of Strong Acid to \(A^-\)
\(f_{HA}\)= 0.91
\(f_{A^-}\) = 0.09
Beginning with one equivalent (eq.) of \(A^-\) (e.g. sodium salt) you would need to add 0.91 eq. of HCl, which would protonate 0.91 eq. of \(A^-\) to HA, generating the desired fractions of each species: \(f_{HA}\)= 0.91, \(f_{A^-}\) = 0.09.
The total number of moles of the weak acid is 0.025 moles/L x 2 L = 0.05 moles. Therefore the amount of strong acid to be added is 0.05 moles x 0.91 = 0.0455 moles. This would be added to 2L of 0.025 M NaA.
This process of pH adjustment is illustrated on the following diagram:
Polyprotic acids:
- Select an acid that has one of its \(pK_a\) values within 1 pH of the desired pH.
- Calculate the fraction protonated and depronated at the desired pH using the selected \(pK_a\)
- Construct the buffer as follows:
- Method A: mix the acid and conjugate base in the ratio defined by the fraction protonated and depronated. The species that you would use depends on the \(pK_a\) that was selected. For example, if you used a diprotic acid, and used the second \(pK_a\), then you would mix NaHA (protonated species) and Na2A (deprotonated species).
- Method B: Addition of strong base. If you used the first \(pK_a\) then add \(f_{(A^-\)}\) equivalents of strong base to a solution of the fully protonated weak acid. If you used the second \(pK_a\), then add 1+\(f_{(A^-\)}\) to the fully protonated acid. The first equivalent converts all of the acid to the singly ionized species, the additional \(f_{(A^-\)}\) generates the correct ratio of protonated and deprotonated species.
- Method C: Addition of strong acid.If you used the last \(pK_a\) then add \(f_{HA}\)equivalents of strong acid to the fully deprotonated weak acid. If you used the next \(pK_a\), then add 1+ \(f_{HA}\)equivalents of strong acid, etc.
learn by doing
Buffer Construction With Polyprotic Acids.
Sample Question: Given 1L of a 0.1 M solution of \(H_3PO_4\), how many moles of NaOH are required to make a buffer with a pH of 12.4? The \(pK_a\) values for phosphate are 2.15, 7.2, 12.4.
Solution:
1. The third \(pK_a\) is selected to calculate the fraction protonated and deprotonated since its buffer region includes the desired pH.
2. The Henderson-Hasselbalch is used to calculate \(f_{HA}\)and \(f_{(A^-\)}\), using a pH of 12.4 and the third \(pK_a\). In this case the pH=\(pK_a\), so \(f_{HA}\)= \(f_{(A^-\)}\)=0.5.
3. The number of equivalents of NaOH to add is 2+ \(f_{(A^-\)}\). The first two equivalents convert all of the \(H_3PO_4\) to \(HPO_4^{2-}\), and the remaining \(f_{(A^-\)}\) equivalents establish the correct ratio of \(HPO_4^{2-}\) and \(PO_4^{3-}\) to give the desired pH. This is illustrated on the titration curve shown on the right.
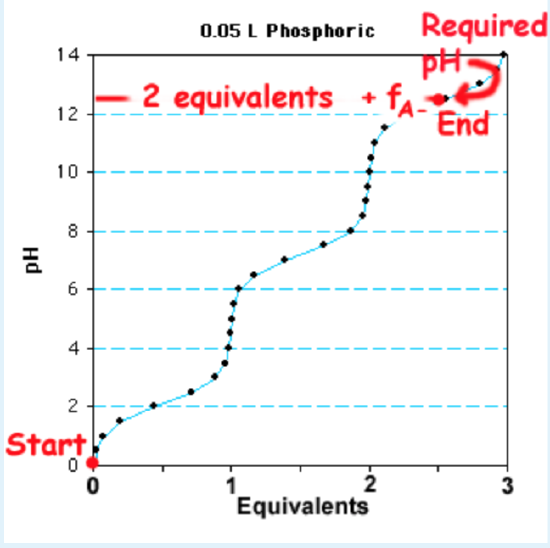
Once the number of equivalents have been determined, the moles of strong base is calculated as:
\[\text { moles }=\text { eq. } \times \left[\mathrm{A}_{\mathrm{T}}\right] \times \mathrm{V}=\left(2+\mathrm{f}_{\mathrm{A}}\right) \times\left[\mathrm{A}_{\mathrm{T}}\right] \times \mathrm{V}\nonumber\]
where V is the total volume of the buffer.
REVIEW QUIZ
did i get this
1. A weak acid can act as a buffer
a. only at body temperatures.
b. at pH values = \(pK_a\) +/- 1.
c. at pH values = \(pK_a\) +/- 2.
d. at pH values = \(pK_a\) +/- 0.1.
e. at any pH value.
- hint
-
The buffering range is shown in the above diagram.
- Answer
-
B. (This is a useful rule-of-thumb.)
2. In the buffer region
a. added base is neutralized by hydronium ions in the solution.
b. the weak acid is fully protonated.
c. the weak acid is fully deprotonated.
d. added acid protonates the conjugate base of the buffer.
e. the ratio of [HA]/[\(A^-\)] is always constant.
Answer
-
d. (The reason solutions of weak acid are buffered around their \(pK_a\) values is because the weak acid can neutralize added base by releasing a proton or neutralize added acid by forming HA; Although the buffer region is characterized by small change in pH, the ration of [HA]/[\(A^-\)] does change.)
3. To make a 1M buffer that has a pH that is one pH unit below the \(pK_a\) of the acid, you would:
a. add equal amounts of the acid and its conjugate base.
b. add 10 fold higher amounts of the acid than the conjugate base.
c. add 10 fold lower amounts of the acid than the conjugate base.
- hint
-
Estimate the ratio of HA to \(A^-\) at the desired pH.
- Answer
-
b. (Since the solution is one pH unit more acidic than the pKa of the acid, you would expect the ratio of [HA]:[\(A^-\)] is equal to 10:1.)

