12.5: Signatures of Selection

How do protein-coding genes evolve?

Think back to what you know of the central dogma, and recall that most amino acids are encoded by more than one codon. Glycine is a great example – when we consider DNA, not RNA, glycine is coded for by GGA, GGT, GGC, and GGG.

Now, let’s imagine we have a GGA codon. What if we change the first base? Well, G->A makes this a serine; G->C makes it an arginine, and G->T makes this codon code for a cysteine. Earlier, we called these mutations “missense” mutations. In this context, we’ll call them nonsynonymous – they change the amino acid that ends up in the protein. Will these mutations be beneficial or deleterious? Without knowing more about the protein, it’s impossible to say. But let’s compare that to changing the LAST base. No matter if we change it to a T, a C or a G, the amino acid REMAINS a glycine. Again, we used to call these mutations “silent” -- but here, we’ll call them synonymous. They don’t change the amino acid that ends up in the protein; they don’t change the organism’s phenotype; and thus they are selectively neutral.

With this in mind, then, let’s consider two sequences of DNA, in two different species, that code for an orthologous protein. We can safely assume that mutations occur at a constant rate across the sequence – that is, in any individual, any of these bases is equally likely to mutate. Remember, though, that there’s a difference between a mutation occurring and those mutations accumulating. For a mutation to accumulate, it has to occur, then get fixed across all the individuals in the population.

But now we have a bunch of sites where any mutation will be synonymous – we'll call these synonymous sites. And we also have a bunch of sites where any mutation will be nonsynonymous – we'll call these mutations nonsynonymous sites. And now we can ask – for all the differences that we saw between these two orthologous genes, what proportion occurred at synonymous sites? We’ll call this proportion Ks. Alternately, what proportion occurred at nonsynonymous sites? Because these mutations resulted in a different amino acid being incorporated into the protein, we’ll call this proportion Ka.

Why are these values, Ks and Ka, interesting? They’re interesting because they can actually tell us about the selective history at this gene! Remember, Ks is a measure of the rate of selectively neutral mutation, while Ka is a measure of the rate of mutations that could change the phenotype – and thus, could be selected for or selected against. If these rates are the same – if Ka equals Ks – then this protein is evolving neutrally. Amino acid changes don’t seem to be selected for or selected against – this may even be a pseudogene, which doesn’t actually end up being made into a protein by the cell. However, let’s imagine that Ka is a lot less than Ks. That means that amino-acid-changing mutations are much less common than silent mutations. One common interpretation of this is that these mutations were usually deleterious to the organism – and that means this gene is really important! For example, a gene encoding a histone might fall into this camp. 

It’s the other possibility that I find most interesting, though. If Ka is substantially MORE than Ks, that means that mutations that changed amino acids were selectively advantageous! They got fixed more frequently than synonymous mutations which are selectively neutral. This is one genomic signal of positive selection – but it’s not the only one. A region of high linkage disequilibrium is another.

How does recent selection show up in the genome?

Let’s imagine that a mutation occurs in a protein-coding gene – we'll say that site A mutates, and the new allele is now called A1. If allele A1 confers a strong selective advantage, then it leads to individuals carrying the mutation to have many more offspring to whom they transmit it. As we saw in the last chapter, this new allele will rapidly increase in frequency in the population. Eventually, it will become fixed – but until then, there are now two alleles at this site in the genome. Recall that we call these sites, where there are two or more common alleles, polymorphic.

Think back to the beginning of the semester and our discussion of how DNA varies, and recall that polymorphisms are very common! In fact, single-nucleotide polymorphisms, or SNPs, are so common that there’s a polymorphic SNP, on average, once every 300 bases in the human genome. And the human genome is 3 billion bases long – so that’s approximately 10 million SNPs!

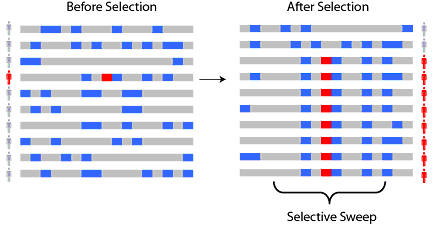
Now return your attention to our new mutation that’s under selection. What happens to other polymorphisms in the area? Remember that it’s not polymorphisms that get transmitted from parents to offspring, it’s chromosomes. And so, our highly advantageous allele will get transmitted alongside all of the other alleles of the other polymorphisms on the same chromosome. Recall that a group of polymorphisms that co-segregate, we call a haplotype. And yes, recombination will eventually separate all of those alleles -- but if the selection is quite strong, the surrounding alleles also increase in frequency alongside the allele that’s under selection. We call this process a selective sweep, because it causes a local decrease in the genetic diversity in the region of the chromosome around the allele that’s being selected for.

Let’s pause and appreciate this connection. Selection is something that causes evolution of a species – but this selection results in a selective sweep, which is a process that happens at the nucleotide level. Finding a selective sweep in a population is an indication that that region of the genome was recently subject to strong positive selection! And we can go looking for these signals using a quantity called linkage disequilibrium.

To help us see how, let’s consider two polymorphisms, A and B. Each has two alleles – polymorphism A has alleles A1 and A2, with population frequencies f(A1) and f(A2). Similarly, polymorphism B has alleles B1 and B2, with population-wide frequencies f(B1) and f(B2).

If we genotyped lots of individuals in the population, and the two polymorphisms segregated completely independently – ie, they were unlinked – then we would expect the frequency of any two alleles to simply be the product of the individual alleles’ frequencies. That is to say, we would expect f(A1,B1) = f(A1)*f(B1). (This is because the probability of two independent events both happening is the probability of the first event happening, times the probability of the second event happening.)

Again, this is what we would expect if the polymorphisms segregating independently. What if these two polymorphisms are linked, one allele is under selection? Let’s say that A1 is under selection, and it is linked to allele B1. If a selective sweep were occurring, we would expect to see A1 and B1 together in an individual more frequently than if they were unlinked. We call this difference linkage disequilibrium, and we define it as D = f(A1,B1) - f(A1)*f(B1). That is to say, it’s the difference between the frequency at which we observe these two alleles together and the frequency we would expect to see them if they were unlinked.

This figure shows a region of high linkage disequilibrium on human chromosome locus 11p13. A red square at the intersection of two SNPs indicates a high linkage disequilibrium between these SNPs. The authors found four common haplotype blocks, outlined in black.

Regions of high linkage disequilibrium are a genomic signature of recent positive selection affecting a polymorphism in that area. And particularly in humans, as we have accumulated more data, both genotypic and phenotypic, we’ve begun to connect regions of high linkage disequilibrium to actual phenotypic examples of traits that imparted selective advantages to historic populations of homo sapiens.

 

Sources:

https://slideplayer.com/slide/14145643/

https://en.wikipedia.org/wiki/Selective_sweep

https://www.nature.com/wls/content/a...e-sweep-24827/

https://www.ncbi.nlm.nih.gov/books/N...figure/pal.f3/