4.3: Deriving Simple Energy Relationships

Thermodynamic laws lead us to equations that help us understand how energy moves (i.e., flows) between components of the universe. As we’ll discuss, the universe is most easily thought of as a giant closed system within which energy can be transferred and even transduced (i.e., from one form to another) between those components. We can’t measure energy flow in or across an entire universe. But we can isolate bits within the universe so that we can quantify energy as it is transferred or transduced within smaller, more manageable closed systems.

4.3.1. Energy in the Universe: The Universe Is a Closed System

Consider an event, any event. I think we can agree that when stuff happens, the participants in the happening go from an unstable state to a relatively more stable state. For example, you are carrying a bag of marbles, the bag tears open, the marbles fall to the floor, then roll and spread out, eventually coming to a stop. At that point, the marbles are in a more stable state than they were when you were holding the un-ripped bag.

We can all agree that gravity made the marbles fall out of the bag. We might further agree to say that the fallen marbles are in a more stable state than they were in the bag in your hands. That much certainly seems true. If so, we could extend our observation to conclude that the drive to greater stability is what made the marbles fall! In fact, regardless of the force or impetus for the event, science does say that the drive to achieve greater stability is what makes stuff (i.e., events) happen!

This is the essence of the second law of thermodynamics: all universal energy-transfer events occur with an increase in stability—that is, an increase in entropy. We’ll consider the second law and entropy in detail shortly.

The tendency of things to go from unstable to more stable is a natural, rational state of affairs, as seen with those marbles on the floor or a messy bedroom with clothes strewn about. Intuitively, mess and disorder are more stable than is a state of order. Of course, marbles dropping or clothing going from folded and hung to wrinkled on the floor releases energy (potential energy) as they fall (kinetic energy). If you don’t believe that this release of energy is real, just think of how much energy you will need to pick up the marbles or to refold your clothes (after laundering them of course!).

We can model the flow of energy in the universe in a way that is consistent with the laws of thermodynamics. Since the first law of thermodynamics says that energy can be neither created nor destroyed, a simple statement of the first law could be the following:

\[\mathbf{E}_{\text {universal }}=\mathrm{E}_{\text {light }}+\mathrm{E}_{\text {heat }}+\mathrm{E}_{\text {electrical }}+\mathrm{E}_{\text {mass }}+\ldots \nonumber\]

This equation sums up the different kinds of energy in the universe. In Figure 4.1, consider the circle (also called a Venn diagram) to be the universe.

Figure 4.1: Venn diagram depicting all things in the universe including mass and more familiar kinds of energy. The diagram implies a as a "closed system"; nothing (mass, energy) can enter or exit the universe, consistent with the first law of thermodynamics.

From this we conclude that energy cannot get into or out of the universe, but energy can be transferred within the universe from one place to another or converted from one form to another. It follows then that \(E_{\rm universal}\) is the sum of all kinds of energy in the universe and that this sum is a constant—in other words, universal energy is conserved; in the words of the first law, universal energy is constant. The following equation expresses this idea; it is a statement of the first law of thermodynamics:

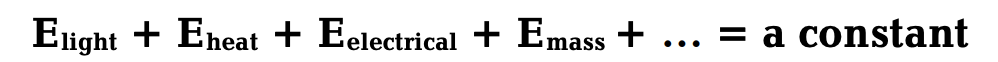
139 First Law of Thermodynamics

In the late nineteenth century, John Venn formalized this visual approach to segregating things and concepts into circles as a way of logically viewing relationships between them. The Venn diagrams used in the following figures are simple and help clarify concepts of energy in the universe. For more complex examples showing overlapping components of the universe (i.e., those that share some but not all attributes), google “Venn diagrams.” For our purposes, let’s stay simple and go with the simpler binary notion of useful and useless energy, our equation shortens to the sum of just two kinds of energy in the universe:

In this equation, G is useful energy; it stands for “Gibbs” free energy, named after Josiah W. Gibbs, who is credited with applying the inductive scientific method to the study of thermodynamics. S is useless energy (entropy), and T is absolute temperature (included because of the third law). This equation is also a statement of the first law, and it is shown in the revised Venn diagram in Figure 4.2.

Figure 4.2: Since even mass is a form of energy, the universe depicted at the left consists of only two components: entropy and free energy (defined as energy that is available to do work. The universe redrawn at the right just redefines free energy as the useful kind, and entropy as useless energy (the opposite of useful!). Both models are still consistent with the first law of thermodynamics.

In this binary energy model, it follows that as universal entropy increases, free energy in the universe must decrease (as graphed in Figure 4.3).

Figure 4.3: Entropy and free energy have a reciprocal relationship, which is graphed here as it changes over time. If all activities in the universe proceed by increasing entropy, and if the universe consists only of free energy and entropy, then as entropy increases, free energy must be decreasing in the universe.

Free or potentially useful energy is higher in more ordered and complex and therefore relatively unstable systems. Such unstable, ordered systems will release free energy spontaneously. In other words, stuff (i.e., spontaneous reactions) will happen!

140-2 Second Law of Thermodynamics

4.3.2. Energy Is Exchanged Between Systems in the Universe

While the arithmetic statements about changes in energy are useful concepts, the parameters are, of course, not measurable! But if we isolate a bit of the universe, we can measure energies and watch energy flow. If we can measure the amount of energy put into or removed from a system within the universe, we can write a more useful equation to follow the transfer of energy between a system and its surroundings:

\(\Delta H = \Delta G + T \Delta S\)

In this formula, \(\Delta H\) is the change (\(\Delta\)) in enthalpy, (i.e., it is the energy entering/leaving the system in units of heat energy); \(\Delta G\) is change in free energy; \(\Delta S\) is change in entropy; and T is the absolute temperature in degrees Kelvin (K).

Heat given off in a reaction (or other event) is often confused with entropy. True, much of the increase in entropy that occurs in living things is indeed in the form of random molecular motion, or heat. But remember that heat can have its uses; not all heat is entropic! Hence, it is more interesting (and accurate!) to think of energy in terms of changes in enthalpy, free energy, and entropy during energy transfers. Thus, we must consider the arithmetic of energy transfers to involve not two, but three terms!

According to the equation \(\Delta H = \Delta G + T \Delta S\), interacting systems in our universe would seem to be closed systems. Accordingly, energy put into or taken from the system (\(\Delta H\)) will be exactly balanced by increases or decreases in the other two terms in the equation (\(\delta G\), \(T \Delta S\)).

Recall that we say a system is closed not because it is really closed but because we can isolate it well enough to measure energy flow into and out of it. This or any algebraic equation with three variables is useful since, if you know two of the values you can calculate the third! Here is a simple situation to illustrate the point: If I put a liter of water onto a burner and light the flame, the water gets hot. If the temperature of the liter of water rises by \(1^{\circ} C\), we know that it has absorbed 1,000 calories (1 kilocalorie, or 1 food Calorie) of the heat from the burner.

Since energy interactions depend on physical conditions, such as temperature and air pressure, we need to standardize those conditions when we conduct experiments that measure energy changes in experimentally isolated systems. For more on how this standardization enables the measuring of energy change in chemical reactions (in fact, any energy exchange), go to the following link.

141 Deriving Closed-System Thermodynamics

Turning to bioenergetics, let’s apply the equation \(\Delta H = \Delta G + T \Delta S\) to the conditions in which chemical reactions occur in cells. Because most life on Earth lives at sea level, where the air pressure is 1 atm (atmosphere), typical determinations of \(\Delta H\), \(\Delta G\), and \(T \Delta S\) are made under defined, well-controlled standard conditions that include “unimolar conditions,” an absolute T of \(298^{\circ} K\) (\(25^{\circ} C\)), 1 atm, and a constant pH of 7.0. The latter is defined as such because the pH inside of a typical cell is close to neutral. Our equation for reactions under these standard conditions becomes the following:

\(\Delta H = \Delta Go + T \Delta S\)

\(\Delta Go\) is the standard free energy change for a reaction conducted in a closed system under standard conditions. \(\Delta H\) and \(\Delta S\) are still the enthalpy and entropy changes, but they are determined under standard conditions.

Now what are those “unimolar conditions”? To meet these conditions, you would measure the calories released by burning (oxidizing) a small amount, say 180 mg of glucose. Then just multiply the number of calories released by 1,000 to get \(\Delta H\), which equates to the number of calories that would have been released by burning 180 gm (i.e., the molecular mass, or a whole mole) of the stuff.

CHALLENGE

From the information provided here, answer the following: What is the molecular weight of glucose? What is the mass of a mole of glucose? And how many moles of glucose were burned?

Now we are ready to consider examples of how we determine the energetics of reactions.

4.3.3. How is Enthalpy (\(\Delta H\)) Determined?

\(\Delta H\) (the heat released or absorbed) in a chemical reaction can easily be determined by conducting the reaction under standard conditions in a bomb calorimeter, which is essentially an inner chamber surrounded by an outer chamber filled with water (Figure 4.4).

Figure 4.4: Basic design of a bomb calorimeter, with an inner chamber for conducting reactions and an outer chamber containing water with a thermometer to measure temperature change (heat absorption or release, or \(\Delta H\)) during the reaction.

Food manufacturers determine the Calorie content of food by bomb calorimetry. As a reaction takes place in the beaker, it will either release or absorb heat, either heating or cooling the water in the calorimeter jacket, as measured by the thermometer. A closed system reaction that releases heat as it reaches equilibrium is defined as exothermic; the \(\Delta H\) for an exothermic reaction is negative. For example, a package says that a chocolate bar has 90 Calories. This means that burning the bar will generate 90 kilocalories (Kcal) of heat as measured in the calorimeter. Recall that 1 Calorie (with a capital C) is equal to 1,000 calories, (1 Kcal). One calorie (cal; lowercase) is the energy needed to raise the temperature of 1 gram of water by one degree Celsius.

You are probably most familiar with reactions that release heat, but some chemical reactions actually absorb heat. Take the common hospital cold pack, for example. Squeeze it to get it going and toss it into the calorimeter; then watch the temperature in the calorimeter drop as the pack absorbs heat from its surroundings! Such reactions are defined as endothermic, with a positive \(\Delta H\). OK, so we can determine the value of one of the energy parameters, but we will need to know at least one other, either \(\Delta Go\) or \(\Delta S\) before the equation \(\Delta H = \Delta Go + T \Delta S\) becomes useful.

4.3.4. How Is Standard Free Energy Change (\(\Delta Go\)) Determined?

As it turns out, \(\Delta Go\) (the standard free energy change) is directly proportional to the concentrations of the reactants and the products of a reaction conducted to completion (i.e., equilibrium) under standard conditions. Therefore, to determine \(\Delta Go\), we need to know or to be able to measure the concentration of reactants and reaction products before and after a chemical reaction (i.e., when the reaction reaches equilibrium). Take the following generic chemical reaction:

\(2A + B <====> 2C + D\)

The Boltzmann equation relates \(\Delta Go\) to equilibrium concentrations of A, B, C, and D:

In this equation, R is the gas constant (1.806 cal/mol-deg); T is \(298^{\circ} K\); and Keq is the equilibrium constant. As you can see, the Keq for the reaction is the ratio of the product of the concentrations of the products (raised to their stoichiometric powers) to the product of the concentrations of the reactants (raised to their stoichiometric powers).

CHALLENGE

Define (or look up) the stoichiometry in chemical reactions.

Once you know (or have determined) the equilibrium concentrations of reactants and products in a chemical reaction, you can use this equation to calculate the \(\Delta Go\) for a reaction. Remember, if the \(\Delta Go\) is a negative number, the reaction is defined as exergonic; i.e., reactions release free energy. Reactions that release fee energy are also referred to as spontaneous reactions. If the \(\Delta Go\) is a positive number, the reaction absorbs free energy. Defined as endergonic, such uphill reactions are not spontaneous.

142 Determining \(\Delta H\) & \(\Delta G\) in Closed Systems

4.3.5. Working an Example Using These Equations for Closed Systems

Consider the following reaction:

\(X \rightleftarrow Y\)

This reaction is endergonic, but if you do not know [X] or [Y] (and therefore don’t know the \(\Delta Go\)), how can you tell? If you are given [X] and [Y], you can also do the math. Assume we measure the concentrations of reactants and products for this reaction at equilibrium, with the following results:

\([X] = 2.5 Kcal/mol\) and \([Y] = 500 cal/mol\)

Try using the Boltzmann equation (in section 4.3.4) to calculate the standard free energy for this reaction. What is the Keq for this reaction? What is the \(\Delta Go\) for the reaction? If you did not come up with a Keq of 0.2 and an absolute value for the standard free energy for |\(\Delta Go\)| of 866.2 Kcal/mol, recalculate or collaborate with a classmate. Hint: make sure that you convert the units in your equation so that they are all the same (e.g., calories to Kcal)! Based on the calculated value of \(\Delta Go\), is this reaction in fact endergonic? Now if you conduct the reaction in a bomb calorimeter, you find that it proceeds to equilibrium with a \(\Delta H = -750 Kcal/mol\). What kind of reaction is this? Together with the enthalpy change, it is now possible to use the equation \(\Delta H = \Delta Go + T \Delta S\) to calculate an absolute value for the entropy change: |\(\Delta S\)| = 116.2 cal/mol-deg for the reaction. At equilibrium, the reaction proceeded with an increase in entropy under standard conditions. Again, if you did not get the correct answer, recalculate, or collaborate with a classmate.

143 Determining \(\Delta S\) in Closed Systems