C12. Free Energy and Cooperativity
- Page ID
- 4974
(a great example of the use of thermodynamic cycles in modern biochemical analysis)
To change the conformation of deoxyHb to oxyHb requires energy (about 6 kcal/mol, or the equivalent of about 2 H-bonds. Remember from our discussion of protein stability, proteins are not inherently all that stable. They denature at modest temperatures, and are stabilized over the native state only about 10 kcal/mol for a typical protein of 100 amino acids. Energy changes in proteins can arise from ligand binding, or tertiary/quaternary structural changes in the protein. Consider the following important points about O2 binding.
- the beta chain of Hb binds O2 noncooperatively, with a Kd similar to Mb.
- the hemoglobin tetramer (T) readily dissociates into alpha-beta dimers (D), which also bind O2 with high affinity, and noncooperatively.
Hence, when 2D ----> T, there is an energy penalty in the form of a greatly reduced O2 affinity, but what is acquired is the property of cooperativity for O2 binding, which facilitates maximal unloading of O2 under physiological conditions. This cooperativity can be measure as ΔGcoop = ΔGc, where
ΔGc = ΔGO2 bind to tetramer - ΔGO2 bind to same site on dimer, or
ΔGc = ΔGT - ΔGD. The ΔGT and the ΔGD can be determined from the binding isotherms (Y vs [O2] at various dilutions of the tetramer). Then ΔGc can be calculated. The results are shown below.
Table 1: Free Energy of Oxygen Binding to Hb T and D.
The tables above show the ΔGc for oxygen binding to various states of Hb. Notice that ΔGc is positive for the first 3 bindings, and negative for the last.
The cooperativity models for oxygen-Hb binding (the MWC -concerted model and the KNF- sequential model) are based on the two end states (fully ligated and fully unligated) and the stepwise states (1, 2, or 3 O2 bound). They do not describe binding to specific sites on the Hb tetramer. That is, they do not reflect the different possible microstates. For example, there are 4 different microstates possible in which 2 O2 are bound to the tetramer (see Table 1). There are 8 different possible partially liganded microstates (Table 1). It has been difficult to study each of these microstates directly since it is impossible to isolate them in pure form, or to resolve their different properties in a mixture. Three reasons account for this:
- each state is labile and O2 exchanges among the states
- the tetramer (T) dissociates to 2D which reassociates to give hybrids.
- the lower relative abundance of intermediates in a cooperative system.
This problem was solved by suing CO, NO, and CN as ligands, since they bind more tightly. Also the Fe can be replaced with Co(II) or Mn (III). We have studied linked equilibrium before:
- 2 N-methylacetamide monomers (aq) ---> N-methylacetamide H-bonded dimer (nonpolar)
- deoxyHb <---> oxyHb in the presence of H+ and CO2 (see above)
We have seen, especially in the former case how thermodynamic cycles or linked equilibria can be used to calculate ΔG and K's for reactions which would be difficult to carry out. Let us now apply these concepts to Hb binding to ligands. Specifically, we wish to calculate ΔGc from the Δ Gs for binding of a ligand to a specific site on a dimer and on the tetramer, as shown below.
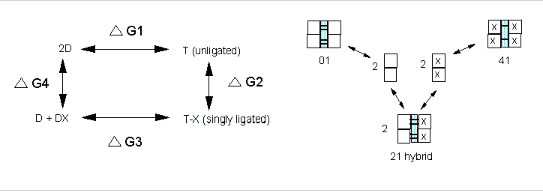
It should be obvious that:
ΔGo1 + ΔGo2 = ΔGo3 + ΔGo4 , or ΔGo3 - ΔGo1 = ΔGo2 - ΔGo4 = ΔGoc . It is not difficult to determine ΔGo3 - ΔGo1 which can be determined using gel filtration chromatography since dimers can readily be separated from tetramers. Methods can be developed to prepare individual microstates and then the assembly free energy can be determined. From this, using thermodynamic cycles, the ΔGoc can be calculated. The results for a Cyanomet Hb microstates are shown in Table 2. The 10 microstates are distributed into 3 distinct cooperative free energies. This suggests that there may be a problem with the MWC model which proposes 2 quaternary states, the T and the R. Is there a third quaternary state, or is there a change in the tertiary structure of the R or T states which generate 3 kcal/mol of cooperative free energy? If the unligated "deoxy"state is the T state, and if the microstates 11,12, and 21 are also assigned to the T state, then the T -->R transition occurs when binding creates a tetramer with 1 or more ligated subunits on each side of the dimer/dimer interface.
The overall ΔGc is generated by two different conformational changes. On binding the first ligand, global conformational changes occur in the ligated dimeric state. The D/D interface acts as a structural constraint against which tertiary structure changes. When oxygen binds to the dissociated dimer, it does not produce a tertiary structural change since there is no interface to oppose the ligand. This strained tertiary conformation raises the energy by +3 kcal/mol. The second conformational change produces a global quaternary change, as the salt bridges break and the T state changes to the R state.
The formation and release of the tertiary constraint is the driving force of cooperative ligand binding. The strength of the T interface is overcome ony when unfavorable ligand induced conformational changes occur in both dimers. The T interface can withstand 1 dimer with the changed tertiary conformation, not 2. The movement of Fe into the plane of the heme ring triggers the tertiary change. The trigger for the quaternary change is the tertiary changes in the dimers.
Now that you understand dioxygen binding, explain the following picture.
![]() Of Mice and Oxygen
Of Mice and Oxygen
![]() Another view
Another view
![]() Liquid breathing
Liquid breathing


