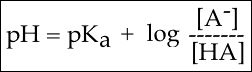Chapter 3: Basics of Biological Chemistry
- Page ID
- 15914
›››
Figure 1. Atoms are the building blocks of molecules found in the universe—air, soil, water, rocks—and also the cells of all living organisms. In this model of an organic molecule, the atoms of carbon (black), hydrogen (white), nitrogen (blue), oxygen (red), and sulfur (yellow) are shown in proportional atomic size. The silver rods represent chemical bonds. (credit: modification of work by Christian Guthier)
The Structure of an atom
An atom is the smallest unit of matter that retains all of the chemical properties of an element. Elements are forms of matter with specific chemical and physical properties that cannot be broken down into smaller substances by ordinary chemical reactions.
The chemistry discussed in BIS2A requires us to use a model for an atom. While there are more sophisticated models, the atomic model used in this course makes the simplifying assumption that the standard atom is composed of three subatomic particles, the proton, the neutron, and the electron. Protons and neutrons have a mass of approximately one atomic mass unit (a.m.u.). One atomic mass unit is approximately 1.660538921 x 10-27kg—roughly 1/12 of the mass of a carbon atom (see table below for more precise value). The mass of an electron is 0.000548597 a.m.u. or 9.1 x 10-31kg. Neutrons and protons reside at the center of the atom in a region call the nucleus while the electrons orbit around the nucleus in zones called orbitals, as illustrated below. The only exception to this description is the hydrogen (H) atom, which is composed of one proton and one electron with no neutrons. An atom is assigned an atomic number based on the number of protons in the nucleus. Neutral carbon (C), for instance has six neutrons, six protons, and six electrons. It has an atomic number of six and a mass of slightly more than 12 a.m.u.
Table 1. Charge, mass, and location of subatomic particles
| Protons, neutrons, and electrons | ||||
| Charge | Mass (a.m.u.) | Mass (kg) | Location | |
| Proton | +1 | ~1 | 1.6726 x 10-27 | nucleus |
| Neutron | 0 | ~1 | 1.6749 x 10-27 | nucleus |
| Electron | –1 | ~0 | 9.1094 x 10-31 | orbitals |
Table 1 reports the charge and location of three subatomic particles—the neutron, proton, and electron. Atomic mass unit = a.m.u. (a.k.a. dalton [Da])—this is defined as approximately one twelfth of the mass of a neutral carbon atom or 1.660538921 x 10−27 kg. This is roughly the mass of a proton or neutron.

Figure 2. Elements, such as helium depicted here, are made up of atoms. Atoms are made up of protons and neutrons located within the nucleus and electrons surrounding the nucleus in regions called orbitals. (Note: This figure depicts a Bohr model for an atom—we could use a new open source figure that depicts a more modern model for orbitals. If anyone finds one please forward it.)
Source:(https://commons.wikimedia.org/wiki/F...um_atom_QM.svg)
By User: Yzmo (Own work) [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], via Wikimedia Commons
Relative sizes and distribution of elements
The typical atom has a radius of one to two angstroms (Å). 1Å = 1 x 10-10m. The typical nucleus has a radius of 1 x 10-5Å or 10,000 smaller than the radius of the whole atom. By analogy, a typical large exercise ball has a radius of 0.85m. If this were an atom, the nucleus would have a radius about 1/2 to 1/10 of your thinnest hair. All of that extra volume is occupied by the electrons in regions called orbitals. For an ideal atom, orbitals are probabilistically defined regions in space around the nucleus in which an electron can be expected to be found.
For additional basic information on atomic structure click here.
For additional basic information on orbitals here.
Video clips
For a review of atomic structure check out this Youtube video: atomic structure.
The properties of living and nonliving materials are determined to a large degree by the composition and organization of their constituent elements. Five elements are common to all living organisms: Oxygen (O), Carbon (C), Hydrogen (H), Phosphorous (P), and Nitrogen (N). Other elements like Sulfur (S), Calcium (Ca), Chloride (Cl), Sodium (Na), Iron (Fe), Cobalt (Co), Magnesium, Potassium (K), and several other trace elements are also necessary for life, but are typically found in far less abundance than the "top five" noted above. As a consequence, life's chemistry—and by extension the chemistry of relevance in BIS2A—largely focuses on common arrangements of and reactions between the "top five" core atoms of biology.
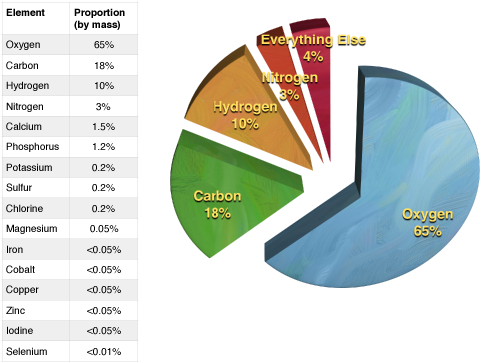
Figure 3. A table illustrating the abundance of elements in the human body. A pie chart illustrating the relationships in abundance between the four most common elements.
Credit: Data from Wikipedia (http://en.wikipedia.org/wiki/Abundan...mical_elements); chart created by Marc T. Facciotti
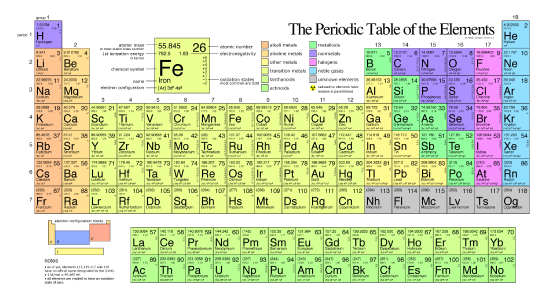
The Periodic Table
The different elements are organized and displayed in the periodic table. Devised by Russian chemist Dmitri Mendeleev (1834–1907) in 1869, the table groups elements that, due to some commonalities of their atomic structure, share certain chemical properties. The atomic structure of elements is responsible for their physical properties including whether they exist as gases, solids, or liquids under specific conditions and and their chemical reactivity, a term that refers to their ability to combine and to chemically bond with each other and other elements.
In the periodic table, shown below, the elements are organized and displayed according to their atomic number and are arranged in a series of rows and columns based on shared chemical and physical properties. In addition to providing the atomic number for each element, the periodic table also displays the element’s atomic mass. Looking at carbon, for example, its symbol (C) and name appear, as well as its atomic number of six (in the upper right-hand corner indicating the number of protons in the neutral nucleus) and its atomic mass of 12.11 (sum of the mass of electrons, protons, and neutrons).
Electronegativity
Molecules are collections of atoms that are associated with one another through bonds. It is reasonable to expect—and the case empirically—that different atoms will exhibit different physical properties, including abilities to interact with other atoms. One such property, the tendency of an atom to attract electrons, is described by the chemical concept and term, electronegativity. While several methods for measuring electronegativity have been developed, the one most commonly taught to biologists is the one created by Linus Pauling.
A description of how Pauling electronegativity can be calculated is beyond the scope of BIS2A. What is important to know, however, is that electronegativity values have been experimentally and/or theoretically determined for nearly all elements in the periodic table. The values are unitless and are reported relative to the standard reference, hydrogen, whose electronegativity is 2.20. The larger the electronegativity value, the greater tendency an atom has to attract electrons. Using this scale, the electronegativity of different atoms can be quantitatively compared. For instance, by using Table 1 below, you could report that oxygen atoms are more electronegative than phosphorous atoms.
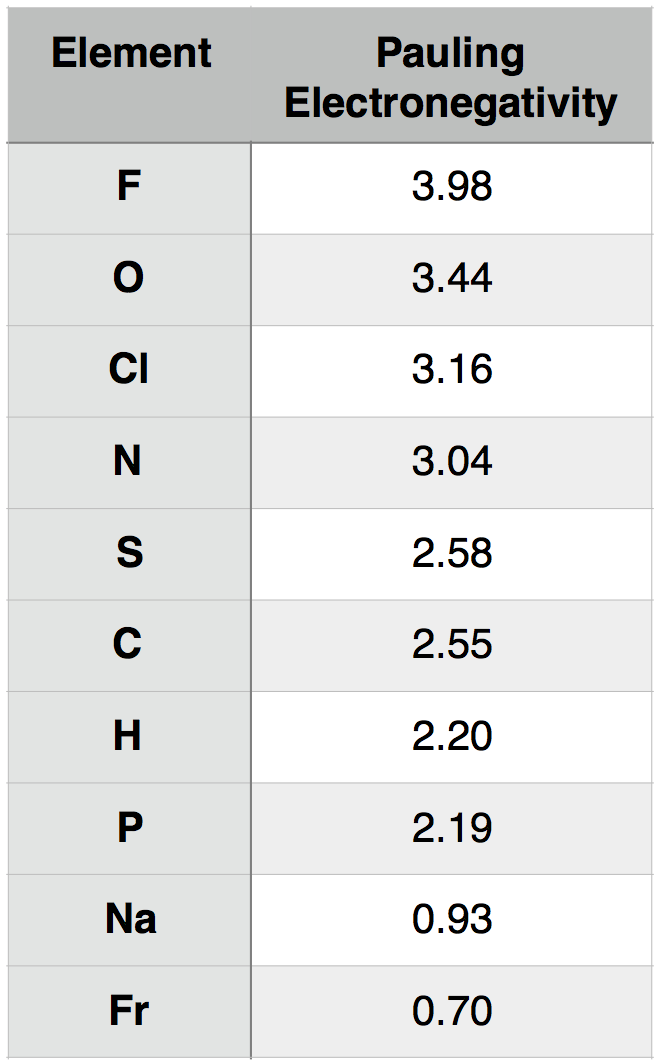
Table 1. Pauling electronegativity values for select elements of relevance to BIS2A as well as elements at the two extremes (highest and lowest) of the electronegativity scale.
Attribution: Marc T. Facciotti (original work)
The utility of the Pauling electronegativity scale in BIS2A is to provide a chemical basis for explaining the types of bonds that form between the commonly occurring elements in biological systems and to explain some of the key interactions that we observe routinely. We develop our understanding of electronegativity-based arguments about bonds and molecular interactions by comparing the electronegativities of two atoms. Recall, the larger the electronegativity, the stronger the "pull" an atom exerts on nearby electrons.
We can consider, for example, the common interaction between oxygen (O) and hydrogen (H). Let us assume that O and H are interacting (forming a bond) and write that interaction as O-H, where the dash between the letters represents the interaction between the two atoms. To understand this interaction better, we can compare the relative electronegativity of each atom. Examining the table above, we see that O has an electronegativity of 3.44, and H has an electronegativity of 2.20.
Based on the concept of electronegativity as we now understand it, we can surmise that the oxygen (O) atom will tend to "pull" the electrons away from the hydrogen (H) when they are interacting. This will give rise to a slight but significant negative charge around the O atom (due to the higher tendency of the electrons to be associated with the O atom). This also results in a slight positive charge around the H atom (due to the decrease in the probability of finding an electron nearby). Since the electrons are not distributed evenly between the two atoms AND, by consequence, the electric charge is also not evenly distributed, we describe this interaction or bond as polar. There are two poles in effect: the negative pole near the oxygen and the positive pole near the hydrogen.
To extend the utility of this concept, we can now ask how an interaction between oxygen (O) and hydrogen (H) differs from an interaction between sulfur (S) and hydrogen (H). That is, how does O-H differ from S-H? If we examine the table above, we see that the difference in electronegativity between O and H is 1.24 (3.44 - 2.20 = 1.24) and that the difference in electronegativity between S and H is 0.38 (2.58 – 2.20 = 0.38). We can therefore conclude that an O-H bond is more polar than an S-H bond. We will discuss the consequences of these differences in subsequent chapters.
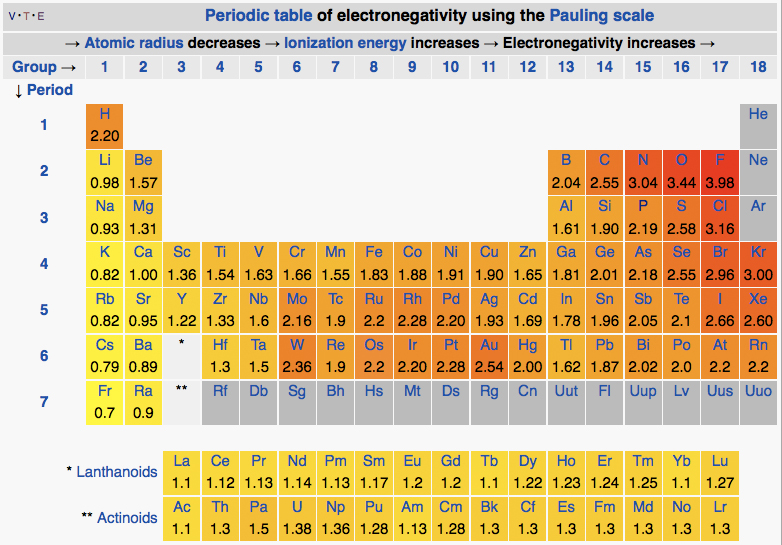
Figure 2. The periodic table with the electronegativities of each atom listed.
Attribution: By DMacks (https://en.wikipedia.org/wiki/Electronegativity) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons
An examination of the periodic table of the elements (Figure 2) illustrates that electronegativity is related to some of the physical properties used to organize the elements into the table. Certain trends are apparent. For instance, those atoms with the largest electronegativity tend to reside in the upper right hand corner of the periodic table, such as Fluorine (F), Oxygen (O) and Chlorine (Cl), while elements with the smallest electronegativity tend to be found at the other end of the table, in the lower left, such as Francium (Fr), Cesium (Cs) and Radium (Ra).
More information on electronegativity can be found in the LibreTexts.
The main use of the concept of electronegativity in BIS2A will therefore be to provide a conceptual grounding for discussing the different types of chemical bonds that occur between atoms in nature. We will focus primarily on three types of bonds: Ionic Bonds, Covalent Bonds and Hydrogen Bonds.
Bond types
In BIS2A, we focus primarily on three different bond types: ionic bonds, covalent bonds, and hydrogen bonds. We expect students to be able to recognize each different bond type in molecular models. In addition, for commonly seen bonds in biology, we expect student to provide a chemical explanation, rooted in ideas like electronegativity, for how these bonds contribute to the chemistry of biological molecules.
Ionic bonds
Ionic bonds are electrostatic interactions formed between ions of opposite charges. For instance, most of us know that in sodium chloride (NaCl) positively charged sodium ions and negatively charged chloride ions associate via electrostatic (+ attracts -) interactions to make crystals of sodium chloride, or table salt, creating a crystalline molecule with zero net charge. The origins of these interactions may arise from the association of neutral atoms whose difference in electronegativities is sufficiently high. Take the example above. If we imagine that a neutral sodium atom and a neutral chlorine atom approach one another, it is possible that at close distances, due to the relatively large difference in electronegativity between the two atoms, that an electron from the neutral sodium atom is transferred to the neutral chlorine atom, resulting in a negatively charged chloride ion and a positively charged sodium ion. These ions can now interact via an ionic bond.

Figure 1. The formation of an ionic bond between sodium and chlorine is depicted. In panel A, a sufficient difference in electronegativity between sodium and chlorine induces the transfer of an electron from the sodium to the chlorine, forming two ions, as illustrated in panel B. In panel C, the two ions associate via an electrostatic interaction. Attribution: By BruceBlaus (own work) [CC BY-SA 4.0 (http://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons
This movement of electrons from one atom to another is referred to as electron transfer. In the example above, when sodium loses an electron, it now has 11 protons, 11 neutrons, and 10 electrons, leaving it with an overall charge of +1 (summing charges: 11 protons at +1 charge each and 10 electrons at -1 charge each = +1). Once charged, the sodium atom is referred to as a sodium ion. Likewise, based on its electronegativity, a neutral chlorine (Cl) atom tends to gain an electron to create an ion with 17 protons, 17 neutrons, and 18 electrons, giving it a net negative (–1) charge. It is now referred to as a chloride ion.
We can interpret the electron transfer above using the concept of electronegativity. Begin by comparing the electronegativities of sodium and chlorine by examining the periodic table of elements below. We see that chlorine is located in the upper-right corner of the table, while sodium is in the upper left. Comparing the electronegativity values of chlorine and sodium directly, we see that the chlorine atom is more electronegative than is sodium. The difference in the electronegativity of chlorine (3.16) and sodium (0.93) is 2.23 (using the scale in the table below). Given that we know an electron transfer will take place between these two elements, we can conclude that differences in electronegativities of ~2.2 are large enough to cause an electron to transfer between two atoms and that interactions between such elements are likely through ionic bonds.

Figure 2. The periodic table of the elements listing electronegativity values for each element. The elements sodium and chlorine are boxed with a teal boundary. Attribution: By DMacks (https://en.wikipedia.org/wiki/Electronegativity) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons—Modified by Marc T. Facciotti
Note: possible discussion
The atoms in a 5 in. x 5 in. brick of table salt (NaCl) sitting on your kitchen counter are held together almost entirely by ionic bonds. Based on that observation, how would you characterize the strength of ionic bonds?
Now consider that same brick of table salt after having been thrown into an average backyard swimming pool. After a couple of hours, the brick would be completely dissolved, and the sodium and chloride ions would be uniformly distributed throughout the pool. What might you conclude about the strength of ionic bonds from this observation?
Propose a reason why NaCl's ionic bonds in air might be behaving differently than those in water? What is the significance of this to biology?
For additional information:
Check out the link from the Khan Academy on ionic bonds.
Covalent bonds
We can also invoke the concept of electronegativity to help describe the interactions between atoms that have differences in electronegativity too small for the atoms to form an ionic bond. These types of interactions often result in a bond called a covalent bond. In these bonds, electrons are shared between two atoms—in contrast to an ionic interaction in which electrons remain on each atom of an ion or are transferred between species that have highly different electronegativities.
We start exploring the covalent bond by looking at an example where the difference in electronegativity is zero. Consider a very common interaction in biology, the interaction between two carbon atoms. In this case, each atom has the same electronegativity, 2.55; the difference in electronegativity is therefore zero. If we build our mental model of this interaction using the concept of electronegativity, we realize that each carbon atom in the carbon-carbon pair has the same tendency to "pull" electrons to it. In this case, when a bond is formed, neither of the two carbon atoms will tend to "pull" (a good anthropomorphism) electrons from the other. They will "share" (another anthropomorphism) the electrons equally, instead.
Aside: bounding example
The two examples above—(1) the interaction of sodium and chlorine, and (2) the interaction between two carbon atoms—frame a discussion by "bounding," or asymptotic analysis (see earlier reading). We examined what happens to a physical system when considering two extremes. In this case, the extremes were in electronegativity differences between interacting atoms. The interaction of sodium and chlorine illustrated what happens when two atoms have a large difference in electronegativities, and the carbon-carbon example illustrated what happens when that difference is zero. Once we create those mental goal posts describing what happens at the extremes, it is then easier to imagine what might happen in between—in this case, what happens when the difference in electronegativity is between 0 and 2.2. We do that next.
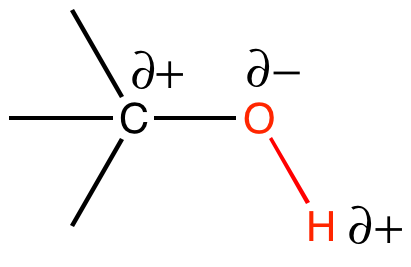
When the sharing of electrons between two covalently bonded atoms is nearly equal, we call these bonds nonpolar covalent bonds. If by contrast, the sharing of electrons is not equal between the two atoms (likely due to a difference in electronegativities between the atoms), we call these bonds polar covalent bonds.
In a polar covalent bond, the electrons are unequally shared by the atoms and are attracted to one nucleus more than to the other. Because of the unequal distribution of electrons between atoms in a polar covalent bond, a slightly positive (indicated by δ+) or slightly negative (indicated by δ–) charge develops at each pole of the bond. The slightly positive (δ+) charge will develop on the less electronegative atom, as electrons get pulled more towards the slightly more electronegative atom. A slightly negative (δ–) charge will develop on the more electronegative atom. Since there are two poles (the positive and negative poles), the bond is said to possess a dipole.
Examples of nonpolar covalent and polar covalent bonds in biologically relevant molecules
Nonpolar covalent bonds
Molecular oxygen
Molecular oxygen (O2) is made from an association between two atoms of oxygen. Since the two atoms share the same electronegativity, the bonds in molecular oxygen are nonpolar covalent.
Methane
Another example of a nonpolar covalent bond is the C-H bond found in the methane gas (CH4). Unlike the case of molecular oxygen where the two bonded atoms share the same electronegativity, carbon and hydrogen do not have the same electronegativity; C = 2.55 and H = 2.20—the difference in electronegativity is 0.35.

Figure 3. Molecular line drawings of molecular oxygen, methane, and carbon dioxide. Attribution: Marc T. Facciotti (own work)
Some of you may now be confused. If there is a difference in electronegativity between the two atoms, is the bond not by definition polar? The answer is both yes and no and depends on the definition of polar that the speaker/writer is using. Since this is an example of how taking shortcuts in the use of specific vocabulary can sometimes lead to confusion, we take a moment to discuss this here. See the mock exchange between a student and an instructor below for clarification:
1. Instructor: "In biology, we often say that the C-H bond is nonpolar."
2. Student: "But there is an electronegativity difference between C and H, so it would appear that C should have a slightly stronger tendency to attract electrons. This electronegativity difference should create a small, negative charge around the carbon and a small, positive charge around the hydrogen."
3. Student: "Since there is a differential distribution of charge across the bond, it would seem that, by definition, this should be considered a polar bond."
4. Instructor: "In fact, the bond does have some small polar character."
5. Student: "So, then it's polar? I'm confused."
6. Instructor: "It has some small amount of polar character, but it turns out that for most of the common chemistry that we will encounter that this small amount of polar character is insufficient to lead to "interesting" chemistry. So, while the bond is, strictly speaking, slightly polar, from a practical standpoint it is effectively nonpolar. We therefore call it nonpolar."
7. Student: "That's needlessly confusing; how am I supposed to know when you mean strictly 100% nonpolar, slightly polar, or functionally polar when you use the same word to describe two of those three things?"
8. Instructor: "Yup, it sucks. The fix is that I need to be as clear as I can when I talk with you about how I am using the term "polarity." I also need to inform you that you will find this shortcut (and others) used when you go out into the field, and I encourage you to start learning to recognize what is intended by the context of the conversation.
A real-world analogy of this same problem might be the use of the word "newspaper". It can be used in a sentence to refer to the company that publishes some news, OR it can refer to the actual item that the company produces. In this case, the disambiguation is easily made by native English speakers, as they can determine the correct meaning from the context; non-native speakers may be more confused. Don't worry; as you see more examples of technical word use in science, you'll learn to read correct meanings from contexts too."
Aside:
How large should the difference in electronegativity be in order to create a bond that is "polar enough" that we decide to call it polar in biology? Of course, the exact value depends on a number of factors, but as a loose rule of thumb, we sometimes use a difference of 0.4 as a guesstimate.
This extra information is purely for your information. You will not be asked to assign polarity based on this criteria in BIS2A. You should, however, appreciate the concept of how polarity can be determined by using the concept of electronegativity. You should also appreciate the functional consequences of polarity (more on this in other sections) and the nuances associated with these terms (such as those in the discussion above).
Polar covalent bonds
The polar covalent bond can be illustrated by examining the association between O and H in water (H2O). Oxygen has an electronegativity of 3.44, while hydrogen has an electronegativity of 2.20. The difference in electronegativity is 1.24. It turns out that this size of electronegativity difference is large enough that the dipole across the molecule contributes to chemical phenomenon of interest.
This is a good point to mention another common source of student confusion regarding the use of the term polar. Water has polar bonds. This statement refers specifically to the individual O-H bonds. Each of these bonds has a dipole. However, students will also hear that water is a polar molecule. This is also true. This latter statement is referring to the fact that the sum of the two bond dipoles creates a dipole across the whole molecule. A molecule may be nonpolar but still have some polar bonds.

Figure 4. A water molecule has two polar O-H bonds. Since the distribution of charge in the molecule is asymmetric (due to the number and relative orientations of the bond dipoles), the molecule is also polar. The element name and electronegativities are reported in the respective sphere. Attribution: Marc T. Facciotti (own work)
For additional information, view this short video to see an animation of ionic and covalent bonding.
The continuum of bonds between covalent and ionic
The discussion of bond types above highlights that in nature you will see bonds on a continuum from completely nonpolar covalent to purely ionic, depending on the atoms that are interacting. As you proceed through your studies, you will further discover that in larger, multi-atom molecules, the localization of electrons around an atom is also influenced by multiple factors. For instance, other atoms that are also bonded nearby will exert an influence on the electron distribution around a nucleus in a way that is not easily accounted for by invoking simple arguments of pairwise comparisons of electronegativity. Local electrostatic fields produced by other non-bonded atoms may also have an influence. Reality is always more complicated than are our models. However, if the models allow us to reason and predict with "good enough" precision or to understand some key underlying concepts that can be extended later, they are quite useful.
Key bonds in BIS2A
In BIS2A, we are concerned with the chemical behavior of and bonds between atoms in biomolecules. Fortunately, biological systems are composed of a relatively small number of common elements (e.g., C, H, N, O, P, S, etc.) and some key ions (e.g., Na+, Cl-, Ca2+, K+, etc.). Start recognizing commonly occurring bonds and the chemical properties that we often see them showing. Some common bonds include C-C, C-O, C-H, N-H, C=O, C-N, P-O, O-H, S-H, and some variants. These will be discussed further in the context of functional groups. The task is not as daunting as it seems.
Hydrogen Bonds
When hydrogen forms a polar covalent bond with an atom of higher electronegativity, the region around the hydrogen will have a fractional positive charge (termed δ+). When this fractional positive charge encounters a partial negative charge (termed δ-) from another electronegative atom to which the hydrogen is NOT bound, AND it is presented to that negative charge in a suitable orientation, a special kind of interaction called a hydrogen bond can form. While chemists are still debating the exact nature of the hydrogen bond, in BIS2A, we like to conceive of it as a weak electrostatic interaction between the δ+ of the hydrogen and the δ- charge on an electronegative atom. We call the molecule that contributes the partially charged hydrogen atom "the hydrogen bond donor" and the atom with the partial negative charge the "hydrogen bond acceptor." You will be asked to start learning to recognize common biological hydrogen bond donors and acceptors and to identify putative hydrogen bonds from models of molecular structures.
Hydrogen bonds are common in biology both within and between all types of biomolecules. Hydrogen bonds are also critical interactions between biomolecules and their solvent, water.
Figure 1: Two water molecules are depicted forming a hydrogen bond (drawn as a dashed blue line). The water molecule on top "donates" a partially charged hydrogen while the water molecule on the bottom accepts that partial charge by presenting a complementary negatively charged oxygen atom.
Attribution: Marc T. Facciotti (original work)
Water
Water is a unique substance whose special properties are intimately tied to the processes of life. Life originally evolved in a watery environment, and most of an organism’s cellular chemistry and metabolism occur inside the water-solvated contents of the cell. Water solvates or "wets" the cell and the molecules in it, plays a key role as reactant or product in an innumerable number of biochemical reactions, and mediates the interactions between molecules in and out of the cell. Many of water’s important properties derive from the molecule's polar nature, which can be tracked down to the polar molecules whose dipole originates from its polar covalent bonds between hydrogen and oxygen.
In BIS2A, the ubiquitous role of water in nearly all biological processes is easy to overlook by getting caught up in the details of specific processes, proteins, the roles of nucleic acids, and in your excitement for molecular machines (it'll happen). It turns out, however, that water plays key roles in all of those processes and we will need to continuously stay aware of the role that water is playing if we are to develop a more functional understanding. Be on the lookout and also pay attention when your instructor points this out.
In a liquid state, individual water molecule interact with one another through a network of dynamic hydrogen bonds that are being constantly forming and breaking. Water also interacts with other molecules that have charged functional groups and/or functional groups with hydrogen bond donors or acceptors. A substance with sufficient polar or charged character may dissolve or be highly miscible in water is referred to as being hydrophilic (hydro- = “water”; -philic = “loving”). By contrast, molecules with more nonpolar characters such as oils and fats do not interact well with water and separate from it rather than dissolve in it, as we see in salad dressings containing oil and vinegar (an acidic water solution). These nonpolar compounds are called hydrophobic (hydro- = “water”; -phobic = “fearing”). We will consider the some of the energetic components of these types of reactions in other another chapter.
Figure 1. In a liquid state water forms a dynamic network of hydrogen bonds between individual molecules. Shown are one donor-acceptor pair.
Attribution: Marc T. Facciotti (original work)
Water's solvent properties
Since water is a polar molecule with slightly positive and slightly negative charges, ions and polar molecules can readily dissolve in it. Therefore, water is referred to as a solvent, a substance capable of dissolving other polar molecules and ionic compounds. The charges associated with these molecules will form hydrogen bonds with water, surrounding the particle with water molecules. This is referred to as a sphere of hydration, or a hydration shell and serves to keep the particles separated or dispersed in the water.
When ionic compounds are added to water, the individual ions interact with the polar regions of the water molecules, and the ionic bonds are likely disrupted in the process called dissociation. Dissociation occurs when atoms or groups of atoms break off from molecules and form ions. Consider table salt (NaCl, or sodium chloride). A dry block of NaCl is held together by ionic bonds and is difficult to dissociate. When NaCl crystals are added to water, however, the molecules of NaCl dissociate into Na+ and Cl– ions, and spheres of hydration form around the ions. The positively charged sodium ion is surrounded by the partially negative charge of the water molecule’s oxygen. The negatively charged chloride ion is surrounded by the partially positive charge of the hydrogen on the water molecule. One may imagine a model in which the ionic bonds in the crystal are "traded" for many smaller scale ionic bonds with the polar groups on water molecules.
Figure 2. When table salt (NaCl) is mixed in water, spheres of hydration are formed around the ions. This figure depicts a sodium ion (dark blue sphere) and a chloride ion (light blue sphere) solvated in a "sea" of water. Note how the dipoles of the water molecules surrounding the ions are aligned such that complementary charges/partial charges are associating with one another (i.e., the partial positive charges on the water molecules align with the negative chloride ion whereas the partial negative charges on the oxygen of water align with the positively charged sodium ion).
Attribution: Ting Wang - UC Davis (original work modified by Marc T. Facciotti)
Note: possible discussion
Consider the model of water dissolving a salt crystal presented above. Describe in your own words how this model can be used to explain what is happening at the molecular level when enough salt is added to a volume of water that the salt no longer dissolves (the solution reaches saturation). Work together to craft a common picture.
Tags recommended by the template: article:topic
What is the role of Acid/Base Chemistry in Bis2A?
We have learned that the behavior of chemical functional groups depends greatly on the composition, order and properties of their constituent atoms. As we will see, some of the properties of key biological functional groups can be altered depending on the pH (hydrogen ion concentration) of the solution that they are bathed in.
For example, some of the functional groups on the amino acid molecules that make up proteins can exist in different chemical states depending on the pH. We will learn that the chemical state of these functional groups in the context of a protein can have have a profound effect on the shape of protein or its ability to carry out chemical reactions. As we move through the course we will see numerous examples of this type of chemistry in different contexts.
pH is formally defined as:
In the equation above, the square brackets surrounding \9\ce{indicate concentration. If necessary, try a math review at wiki logarithm or kahn logarithm. Also see: concentration dictionary or wiki concentration.
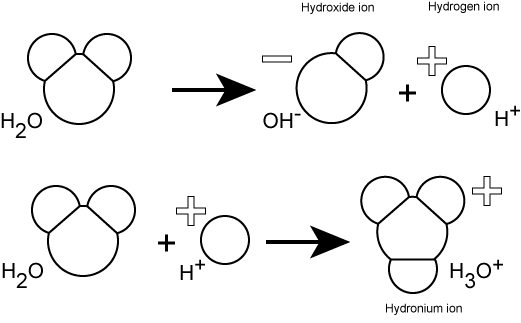
Hydrogen ions are spontaneously generated in pure water by the dissociation (ionization) of a small percentage of water molecules into equal numbers of hydrogen (H+) ions and hydroxide (OH-) ions. While the hydroxide ions are kept in solution by their hydrogen bonding with other water molecules, the hydrogen ions, consisting of naked protons, are immediately attracted to un-ionized water molecules, forming hydronium ions (H30+).
Still, by convention, scientists refer to hydrogen ions and their concentration as if they were free in this state in liquid water. This is another example of a shortcut that we often take - it's easier to write H+ rather than H3O+. We just need to realize that this shortcut is being taken; otherwise confusion will ensue.
The pH of a solution is a measure of the concentration of hydrogen ions in a solution (or the number of hydronium ions). The number of hydrogen ions is a direct measure of how acidic or how basic a solution is.
The pH scale is logarithmic and ranges from 0 to 14 (Figure 2). We define pH=7.0 as neutral. Anything with a pH below 7.0 is termed acidic and any reported pH above 7.0 is termed alkaline or basic. Extremes in pH in either direction from 7.0 are usually considered inhospitable to life, although examples exist to the contrary. pH levels in the human body usually range between 6.8 and 7.4, except in the stomach where the pH is more acidic, typically between 1 and 2.
Watch this video for a straightforward explanation of pH and its logarithmic scale.
Figure 2: The pH scale ranging from acidic to basic with various biological compounds or substances that exist at that particular pH. Attribution: Marc T. Facciotti
For additional information:
Watch this video for an alternative explanation of pH and its logarithmic scale.
The concentration of hydrogen ions dissociating from pure water is 1 × 10-7 moles H+ ions per liter of water.
1 mole (mol) of a substance (which can be atoms, molecules, ions, etc), is defined as being equal to 6.02 x 1023 particles of the substance. Therefore, 1 mole of water is equal to 6.02 x 1023 water molecules. The pH is calculated as the negative of the base 10 logarithm of this unit of concentration. The log10 of 1 × 10-7 is -7.0, and the negative of this number yields a pH of 7.0, which is also known as neutral pH.
Non-neutral pH readings result from dissolving acids or bases in water. High concentrations of hydrogen ions yields a low pH number, whereas low levels of hydrogen ions result in a high pH.
This inverse relationship between pH and the concentration of protons confuses many students - take the time to convince yourself that you "get it."
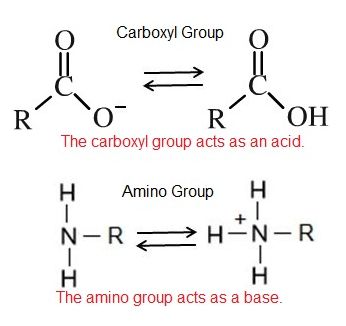
An acid is a substance that increases the concentration of hydrogen ions (H+) in a solution, usually by having one of its hydrogen atoms dissociate. For example, we have learned that the carboxyl functional group is an acid. The hydrogen atom can dissociate from the oxygen atom resulting in a free proton and a negatively charged functional group. A base provides either hydroxide ions (OH–) or other negatively charged ions that combine with hydrogen ions, effectively reducing the H+ concentration in the solution and thereby raising the pH. In cases where the base releases hydroxide ions, these ions bind to free hydrogen ions, generating new water molecules. For example, we have learned that the amine functional group is a base. The nitrogen atom will accept hydrogen ions in solution, thereby reducing the number of hydrogen ions which raises the pH of the solution.
Additional pH resources
Here are some additional links on pH and pKa to help learn the material. Note that there is an additional module devoted to pKa.
Chemwiki Links
Khan Academy Links
Simulations
pKa
pKa is defined as the negative log10 of the dissociation constant of an acid, its Ka. Therefore, the pKa is a quantitative measure of how easily or how readily the acid gives up its proton [H+] in solution and thus a measure of the "strength" of the acid. Strong acids have a small pKa, weak acids have a larger pKa.
The most common acid we will talk about in BIS2A is the carboxylic acid functional group. These acids are typically weak acids, meaning that they only partially dissociate (into H+ cations and RCOO- anions) in neutral solution. HCL (hydrogen chloride) is a common strong acid, meaning that it will fully dissociate into H+ and Cl-.
Note that the key difference in the figure below between a strong acid or base and a weak acid or base is the single arrow (strong) versus a double arrow (weak). In the case of the single arrow you can interpret that by imagining that nearly all reactants have been converted into products. Moreover, it is difficult for the reaction to reverse backwards to a state where the protons are again associated with the molecule there were associated with before. In the case of a weak acid or base, the double-sided arrow can be interpreted by picturing a reaction in which:
- both forms of the conjugate acid or base (that is what we call the molecule that "holds" the proton - i.e. CH3OOH and CH3OO-, respectively in the figure) are present at the same time and
- the ratio of those two quantities can change easily by moving the reaction in either direction.
Figure 1. An example of strong acids and strong bases in their protonation and deprotonation states. The value of their pKa is shown on the left. Attribution: Marc T. Facciotti
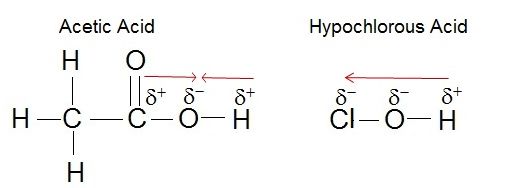
Electronegativity plays a role in the strength of an acid. If we consider the hydroxyl group as an example, the greater electronegativity of the atom or atoms (indicated R) attached to the hydroxyl group in the acid R-O-H results in a weaker H-O bond, which is thus more readily ionized. This means that the pull on the electrons away from the hydrogen atom gets greater when the oxygen atom attached to the hydrogen atom is also attached to another electronegative atom. An example of this is HOCL. The electronegative Cl polarizes the H-O bond, weakening it and facilitating the ionization of the hydrogen. If we compare this to a weak acid where the oxygen is bound to a carbon atom (as in carboxylic acids) the oxygen is bound to the hydrogen and carbon atom. In this case, the oxygen is not bound to another electronegative atom. Thus the H-O bond is not further destabilized and the acid is considered a weak acid (it does not give up the proton as easily as a strong acid).
Figure 2. The strength of the acid can be determined by the electronegativity of the atom the oxygen is bound to. For example, the weak acid Acetic Acid, the oxygen is bound to carbon, an atom with low electronegativity. In the strong acid, Hypochlorous acid, the oxygen atom is bound to an even more electronegative Chloride atom.
Attribution: Erin Easlon
In Bis2A you are going to be asked to relate pH and pKa to each other when discussing the protonation state of an acid or base, for example, in amino acids. How can we use the information given in this module to answer the question: Will the functional groups on the amino acid Glutamate be protonated or deprotonated at a pH of 2, at a pH of 8, at a pH of 11?
In order to start answering this question we need to create a relationship between pH and pKa. The relationship between pKa and pH is mathematically represented by Henderson-Hasselbach equation shown below, where [A-] represents the deprotonated form of the acid and [HA] represents the protonated form of the acid.
Figure 3. The Henderson-Hasselbach equation
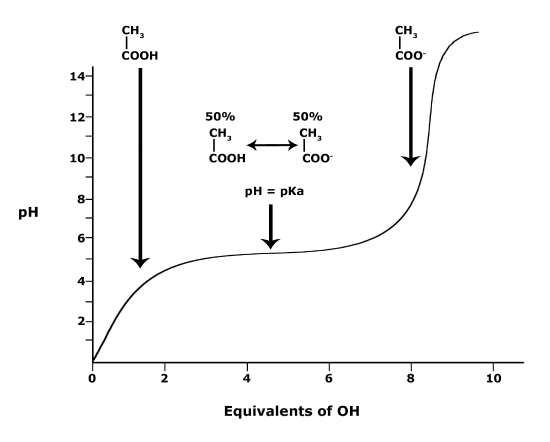
A solution to this equation is obtained by setting pH = pKa. In this case, log([A-] / [HA]) = 0, and [A-] / [HA] = 1. This means that when the pH is equal to the pKa there are equal amounts of protonated and deprotonated forms of the acid. For example, if the pKa of the acid is 4.75, at a pH of 4.75 that acid will exist as 50% protonated and 50% deprotonated. This also means that as the pH rises, more of the acid will be converted into the deprotonated state and at some point the pH will be so high that the majority of the acid will exist in the deprotonated state.
Figure 4. This graph depicts the protonation state of acetic acid as the pH changes. At a pH below the pKa, the acid is protonated. At a pH above the pKa the acid is deprotonated. If the pH equals the pKa, the acid is 50% protonated and 50% deprotonated. Attribution: Ivy Jose
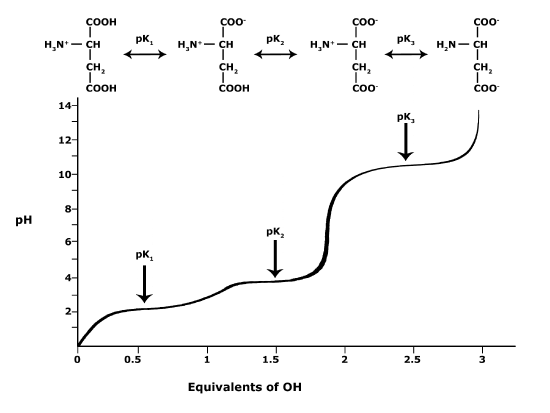
In BIS2A, we will be looking at the protonation state and deprotonation state of amino acids. Amino acids contain multiple functional groups that can be acids or bases. Therefore their protonation/deprotonation status can be more complicated. Below is the relationship between the pH and pKa of the amino acid Glutamic Acid. In this graph we can ask the question we posed earlier: Will the functional groups on the amino acid Glutamate be protonated or deprotonated at a pH of 2, at a pH of 8, at a pH of 11?
Figure 5. This graph depicts the protonation state of glutamate as the pH changes. At a pH below the pKa for each functional group on the amino acid, the functional group is protonated. At a pH above the pKa for the functional group it is deprotonated. If the pH equals the pKa, the functional group is 50% protonated and 50% deprotonated.
Attribution: Ivy Jose
Note: Possible discussion
- What is the overall charge of free Glutamate at a pH of 5?
- What is the overall charge of free Glutamate at a pH of 10?
Chemical reactions
Chemical reactions occur when two or more atoms bond together to form molecules or when bonded atoms are broken apart. The substances that "go into" a chemical reaction are called the reactants (by convention, these are usually listed on the left side of a chemical equation), and the substances that are found to "come out" of the reaction are known as the products (by convention, these are usually found on the right side of a chemical equation). An arrow linking the reactants and products is typically drawn between them to indicate the direction of the chemical reaction. By convention, for one-way reactions, reactants are listed on the left and products on the right of the single-headed arrow. However, you should be able to identify reactants and products of one-way reactions that are written in any orientation (e.g., right-to-left, top-to-bottom, diagonal right-to-left, around a circular arrow, etc.)
\[\underbrace{2H_2O_2}_{\text{hydrogen peroxide}} → \underbrace{2H_2O}_{\text{water}} + \underbrace{O_2}_{\text{oxygen}}\]
Note: practice
Identify the reactants and products of the reaction involving hydrogen peroxide above.
Note: possible discussion
When we write
to represent the molecule hydrogen peroxide, it is a model representing an actual molecule. What information about the molecule is immediately communicated by this molecular formula? That is, what do you know about the molecule just by looking at the term
?
What information is not explicitly communicated about this molecule by looking only at the formula?
Some chemical reactions, such as the one shown above, proceed mostly in one direction. When we depict reactions with a single-headed (unidirectional) arrow, we are implying that the reaction is essentially irreversible. However, all reactions can technically proceed in both directions. Reversible reactions are those that can proceed in either direction. In reversible reactions, reactants are turned into products, but when the concentration of product goes beyond a certain threshold (a characteristic particular to a specific reaction), some of these products will be converted back into reactants. This back and forth continues until a certain relative balance between reactants and products occurs—a state called equilibrium. These situations of reversible reactions are often denoted by a chemical equation with a double-headed arrow pointing towards both the reactants and products. You will find a continuum of chemical reactions; some proceed mostly in one direction and nearly never reverse, while others change direction easily, depending on various factors like the relative concentrations of reactants and products. That is, you will find reactions with all sorts of equilibrium points.
Note: use of vocabulary
You may have realized that the terms "reactants" and "products" are relative to the direction of the reaction. If you have a reaction that is reversible, though, the products of running the reaction in one direction become the reactants of the reverse. You can label the same compound with two different terms. That can be a bit confusing. So, what is one to do in such cases? The answer is that if you want to use the terms "reactants" and "products," you must be clear about the direction of the reaction that you are referring to.
Let's look at an example of a reversible reaction in biology. In human blood, excess hydrogen ions (H+) bind to bicarbonate ions (HCO3-), forming an equilibrium state with carbonic acid (H2CO3). This reaction is readily reversible. If carbonic acid were added to this system, some of it would be converted to bicarbonate and hydrogen ions, as the chemical system seeks equilibrium.
\[HCO_3^−+ H^+ \rightleftharpoons H_2CO_3 \label{2}\]
The examples above examine "idealized" chemical systems as they might occur in a test tube. In biological systems, however, equilibrium for a single reaction is rarely obtained as it might be in the lab. In biological systems, reactions do not occur in isolation. The concentrations of the reactants and/or products are constantly changing, often with a product of one reaction being a reactant for another reaction. These linked reactions form what are known as biochemical pathways. The immediate example above illustrates this and another caveat. While the reaction between the bicarbonate/proton and carbonic acid is highly reversible, it turns out that physiologically this reaction is usually "pulled" towards the formation of carbonic acid. Why? As shown below, carbonic acid becomes a reactant for another biochemical reaction: its conversion to CO2 and H2O. This conversion reduces the concentration of H2CO3, thus pulling the reaction between bicarbonate and H+ to the right. Moreover, a third reaction, the removal of CO2 and H2 from the system, also pulls the reaction further to the right. These kinds of reactions are important contributors to maintaining the H+ homeostasis of our blood.
Characteristic Chemical Reactions
All chemical reactions begin with a reactant—the general term for the one or more substances that enter into the reaction. Sodium and chloride ions, for example, are the reactants in the production of table salt. The one or more substances produced by a chemical reaction are called the product. **Note that there is some "hidden" excitement in the story about table salt involving water that we'll see soon.**
In chemical reactions, the atoms and elements present in the reactant(s) must all also be present in the product(s). Similarly, there can be nothing present in the products that was not present in the reactants. This is because chemical reactions are governed by the law of conservation of mass, which states that matter cannot be created nor destroyed in a chemical reaction. This means that when you examine a chemical reaction, you must try to account for everything that goes in AND make sure that you can find it all in the stuff that comes out!
Just as you can express mathematical calculations in equations such as 2 + 7 = 9, you can use chemical equations to show how reactants become products. By convention, chemical equations are typically read or written from left to right. Reactants on the left are separated from products on the right by a single- or double-headed arrow indicating the direction in which the chemical reaction proceeds. For example, the chemical reaction in which one atom of nitrogen and three atoms of hydrogen produce ammonia would be written as:
\[N + 3H→NH_3.\]
Correspondingly, the breakdown of ammonia into its components would be written as:
\[NH3→N + 3H.\]
Note that in either direction, you find 1 N and 3 Hs on both sides of the equation.
Reversibility
In theory, any chemical reaction can proceed in either direction under the right conditions. Reactants may synthesize into a product that later reverts back to a reactant. Reversibility is also a quality of exchange reactions. For instance, A+BC→AB+C could then reverse to AB+C→A+BC. This reversibility of a chemical reaction is indicated with a double arrow: A+BC⇄AB+C.
Synthesis reactions
Many macromolecules are made from smaller subunits, or building blocks, called monomers. Monomers covalently link to form larger molecules known as polymers. Often, the synthesis of polymers from monomers will also produce water molecules as products of the reaction. This type of reaction is known as dehydration synthesis or condensation reaction.

Figure 1. In the dehydration synthesis reaction depicted above, two molecules of glucose are linked together to form the disaccharide maltose. In the process, a water molecule is formed.
Attribution: Marc T. Facciotti (original work)
In a dehydration synthesis reaction (Figure 1), the hydrogen of one monomer combines with the hydroxyl group of another monomer, releasing a molecule of water. At the same time, the monomers share electrons and form covalent bonds. As additional monomers join, this chain of repeating monomers forms a polymer. Different types of monomers can combine in many configurations, giving rise to a diverse group of macromolecules. Even one kind of monomer can combine in a variety of ways to form several different polymers; for example, glucose monomers are the constituents of starch, glycogen, and cellulose.
In the carbohydrate monomer example above, the polymer is formed by a dehydration reaction; this type of reaction is also used to add amino acids to a growing peptide chain and nucleotides to the growing DNA or RNA polymer. Visit the modules on Amino Acids, Lipids, and Nucleic Acids to see if you can identify the water molecules that are removed when a monomer is added to the growing polymer.
![]()
Figure 2. This depicts, using words, (decorated with functional groups colored in red) a generic dehydration synthesis/condensation reaction.
Attribution: Marc T. Facciotti (original work)
Hydrolysis reactions
Polymers are broken down into monomers in a reaction known as hydrolysis. A hydrolysis reaction includes a water molecule as a reactant (Figure 3). During these reactions, a polymer can be broken into two components: one product carries a hydrogen ion (H+) from the water, while the second product carries the water's remaining hydroxide (OH–).

Figure 3. In the hydrolysis reaction shown here, the disaccharide maltose is broken down to form two glucose monomers with the addition of a water molecule. Note that this reaction is the reverse of the synthesis reaction shown in Figure 1 above.
Attribution: Marc T. Facciotti (original work)
![]()
Figure 4. This depicts using words (decorated with functional groups colored in red) a generic hydrolysis reaction.
Attribution: Marc T. Facciotti (original work)
Dehydration synthesis and hydrolysis reactions are catalyzed, or “sped up,” by specific enzymes. Note that both dehydration synthesis and hydrolysis reactions involve the making and breaking of bonds between the reactants—a reorganization of the bonds between the atoms in the reactants. In biological systems (our bodies included), food in the form of molecular polymers is hydrolyzed into smaller molecules by water via enzyme-catalyzed reactions in the digestive system. This allows for the smaller nutrients to be absorbed and reused for a variety of purposes. In the cell, monomers derived from food may then be reassembled into larger polymers that serve new functions.
Helpful links:
Visit this site to see visual representations of dehydration synthesis and hydrolysis.
Example of Hydrolysis with Enzyme Action is shown in this 3 minute video entitled: Hydrolysis of Sucrose by Sucrase.
Exchange/transfer reactions
We will also encounter reactions termed exchange reactions. In these types of reactions, "parts" of molecules are transferred between one another—bonds are broken to release a part of a molecule and bonds are formed between the released part and another molecule. These enzyme-catalyzed reactions are usually reasonably complex multistep chemical processes.
Figure 5. An exchange reaction in which both synthesis and hydrolysis can occur, chemical bonds are both formed and broken, is depicted using a word analogy.
Directionality of Chemical Reactions
Chemical reactions
Chemical reactions occur when two or more atoms bond together to form molecules or when bonded atoms are broken apart. The substances that "go in" to a chemical reaction are called the reactants (by convention, these are usually listed on the left side of a chemical equation), and the substances found that "come out" of the reaction are known as the products (by convention, these are usually found on the right side of a chemical equation). An arrow linking the reactants and products is typically drawn between them to indicate the direction of the chemical reaction. By convention, for one-way reactions, reactants are listed on the left and products on the right of the single-headed arrow. However, you should be able to identify reactants and products of one-way reactions that are written in any orientation (e.g. right-to-left; top-to-bottom, diagonal right-to-left, around a circular arrow, etc.)
2H2O2 (hydrogen peroxide) → 2H2O (water) + O2 (oxygen)
Note: possible discussion
Practice: Identify the reactants and products of the reaction involving hydrogen peroxide above.
Note: possible discussion
When we write H2O2 to represent the molecule of hydrogen peroxide, it is a model representing an actual molecule. What information about the molecule is immediately communicated by this molecular formula? That is, what do you know about the molecule just by looking at the term H2O2? What information is not explicitly communicated about this molecule by looking only at the formula?
Some chemical reactions, such as the one shown above, proceed mostly in one direction. When we depict reactions with a single-headed (unidirectional) arrow, we are implying that the reaction is essentially irreversible. However, all reactions can technically proceed in both directions. Reversible reactions are those that can proceed in either direction. In reversible reactions, reactants are turned into products, but when the concentration of product goes beyond a certain threshold (a characteristic particular to a specific reaction), some of these products will be converted back into reactants. This back and forth continues until a certain relative balance between reactants and products occurs—a state called equilibrium. These situations of reversible reactions are often denoted by a chemical equation with a double-headed arrow pointing toward both the reactants and the products. You will find a continuum of chemical reactions; some proceed mostly in one direction and nearly never reverse, while others change direction easily depending on various factors like the relative concentrations of reactants and products. That is, you will find reactions with all sorts of equilibrium points.
Use of vocabulary
You may have realized that the terms "reactants" and "products" are relative to the direction of the reaction. If you have a reaction that is reversible, though, the products of running the reaction in one direction become the reactants of the reverse. You can label the same compound with two different terms. That can be a bit confusing. So, what is one to do in such cases? The answer is that if you want to use the terms "reactants" and "products", you must be clear about the direction of reaction that you are referring to.
Let's look at an example of a reversible reaction in biology. In human blood, excess hydrogen ions (H+) bind to bicarbonate ions (HCO3-), forming an equilibrium state with carbonic acid (H2CO3). This reaction is readily reversible. If carbonic acid were added to this system, some of it would be converted to bicarbonate and hydrogen ions as the chemical system sought out equilibrium.
\[HCO_3^−+ H^+\rightleftharpoons H_2CO_3\]
The examples above examine "idealized" chemical systems as they might occur in a test-tube. In biological systems, however, equilibrium for a single reaction is rarely obtained as it might be in the lab. In biological systems, reactions do not occur in isolation. The concentrations of the reactants and/or products are constantly changing, often with a product of one reaction being a reactant for another reaction. These linked reactions form what are known as biochemical pathways. The immediate example below illustrates the point of biochemical pathways and one other caveat. While the reaction between the bicarbonate/proton and carbonic acid is highly reversible, it turns out that, physiologically, this reaction is usually "pulled" toward the formation of carbonic acid. Why? As shown below, carbonic acid becomes a reactant for another biochemical reaction—its conversion to CO2 and H2O. This conversion reduces the concentration of H2CO3, thus pulling the reaction between bicarbonate and H+ to the right. Moreover, a third, unidirectional reaction, the removal of CO2 and H2O from the system, also pulls the reaction further to the right. These kinds of reactions are important contributors to maintaining the H+ homeostasis of our blood.
\[ HCO_3^- + H^+ \rightleftharpoons H_2CO_3 \rightleftharpoons CO_2 + H_20 \rightarrow waste\]
Figure 1. The reaction involving the synthesis of carbonic acid is actually linked to its breakdown into \(CO_2\) and \(H_2O\). These products are then removed from the system/body when they are exhaled. Together, the breakdown of carbonic acid and the act of exhaling the products pull the first reaction to the right.
Contributors
Marc T. Facciotti (Biomedical Engineering, UC Davis)
Chemical equilibrium—Part 1: forward and reverse reactions
Understanding the concept of chemical equilibrium is critical to following several of the discussions that we have in BIS2A and indeed throughout biology and the sciences. It is difficult to completely describe the concept of chemical equilibrium without reference to the energy of a system, but for the sake of simplicity, let’s try anyway and reserve the discussion of energy for another chapter. Let us, rather, begin developing our understanding of equilibrium by considering the reversible reaction below:

Hypothetical reaction #1: A hypothetical reaction involving compounds A, B and D. If we read this from left to right, we would say that A and B come together to form a larger compound: D. Reading the reaction from right to left, we would say that compound D breaks down into smaller compounds: A and B.
We first need to define what is meant by a “reversible reaction.” The term “reversible” simply means that a reaction can proceed in both directions. That is, the things on the left side of the reaction equation can react together to become the things on the right of the equation, AND the things on the right of the equation can also react together to become the things on the left side of the equation. Reactions that only proceed in one direction are called irreversible reactions.
To start our discussion of equilibrium, we begin by considering a reaction that we posit is readily reversible. In this case, it is the reaction depicted above: the imaginary formation of compound D from compounds A and B. Since it is a reversible reaction, we could also call it the decomposition of D into A and B. Let us, however, imagine an experiment in which we watch the reaction proceed from a starting point where only A and B are present.
Example #1: Left-balanced reaction
| Concentration | t=0 | t=1 | t=5 | t=10 | t=15 | t=20 | t=25 | t=30 | t=35 | t=40 |
|---|---|---|---|---|---|---|---|---|---|---|
| [A] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [B] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [C] | 0 | 10 | 20 | 30 | 45 | 38 | 40 | 40 | 40 | 40 |
At time t = 0 (before the reaction starts), the reaction has 100 concentration units of compounds A and B and zero units of compound D. We now allow the reaction to proceed and observe the individual concentrations of the three compounds over time (t=1, 5, 10, 15, 20, 25, 30, 35, and 40 time units). As A and B react, D forms. In fact, one can see D forming from t=0 all the way to t=25. After that time, however, the concentrations of A, B and D stop changing. Once the reaction reaches the point where the concentrations of the components stop changing, we say that the reaction has reached equilibrium. Notice that the concentrations of A, B, and D are not equal at equilibrium. In fact, the reaction seems left balanced so that there is more A and B than D.
Note
****Common student misconception warning****
Many students fall victim to the misconception that the concentrations of a reaction’s reactants and products must be equal at equilibrium. Given that the term equilibrium sounds a lot like the word “equal,” this is not surprising. But as the experiment above tries to illustrate, this is NOT correct!
Example #2: right-balanced reaction
We can examine a second hypothetical reaction, the synthesis of compound J from the compounds E and F.

Hypothetical reaction #2: A hypothetical reaction involving compounds E, F and J. If we read this from left to right, we would say that E and F come together to form a larger compound: J. Reading the reaction from right to left, we would say that compound J breaks down into smaller compounds: E and F.
The structure of hypothetical reaction #2 looks identical to that of hypothetical reaction #1, which we considered above—two things come together to make one bigger thing. We just need to assume, in this case, that E, F, and J have different properties from A, B, and D. Let’s imagine a similar experiment to the one described above and examine this data:
Hypothetical reaction #2: time course
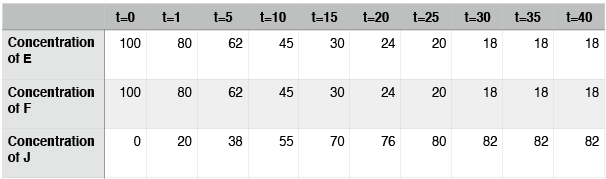
In this case, the reaction also reaches equilibrium. This time, however, equilibrium occurs at around t=30. After that point, the concentrations of E, F, and J do not change. Note again that the concentrations of E, F, and J are not equal at equilibrium. In contrast to hypothetical reaction #1 (the ABD reaction), this time the concentration of J, the thing on the right side of the arrows, is at a higher concentration than E and F. We say that, for this reaction, equilibrium lies to the right.
Four more points need to be made at this juncture.
Point 1: Whether equilibrium for a reaction lies to the left or the right will be a function of the properties of the components of the reaction and the environmental conditions that the reaction is taking place in (e.g., temperature, pressure, etc.).
Point 2: We can also talk about equilibrium using concepts of energy, and we will do this soon, just not yet.
Point 3: While hypothetical reactions #1 and #2 appear to reach a point where the reaction has “stopped,” you should imagine that reactions are still happening even after equilibrium has been reached. At equilibrium the “forward” and “reverse” reactions are just happening at the same rate. That is, in example #2, at equilibrium J is forming from E and F at the same rate that it is breaking down into E and F. This explains how the concentrations of the compounds aren’t changing despite the fact that the reactions are still happening.
Point 4: From this description of equilibrium, we can define something we call the equilibrium constant. Typically, the constant is represented by an uppercase K and may be written as Keq. In terms of concentrations, Keq is written as the mathematical product of the reaction product concentrations (stuff on the right) divided by the mathematical product of the reactant concentrations (stuff on the left). For example, Keq,1 = [D]/[A][B], and Keq,2 = [J]/[E][F]. The square brackets "[]" indicate the “concentration of” whatever is inside the bracket.
Chemical Equilibrium—Part 2: Free Energy
In a previous section, we began a description of chemical equilibrium in the context of forward and reverse rates. Three key ideas were presented:
- At equilibrium, the concentrations of reactants and products in a reversible reaction are not changing in time.
- A reversible reaction at equilibrium is not static—reactants and products continue to interconvert at equilibrium, but the rates of the forward and reverse reactions are the same.
- We were NOT going to fall into a common student trap of assuming that chemical equilibrium means that the concentrations of reactants and products are equal at equilibrium.
Here we extend our discussion and put the concept of equilibrium into the context of free energy, also reinforcing the Energy Story exercise of considering the "Before/Start" and "After/End" states of a reaction (including the inherent passage of time).
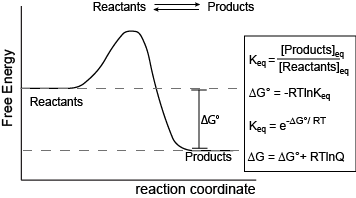
Figure 1. Reaction coordinate diagram for a generic exergonic reversible reaction. Equations relating free energy and the equilibrium constant: R = 8.314 J mol-1 K-1 or 0.008314 kJ mol-1 K-1; T is temperature in Kelvin.
Attribution: Marc T. Facciotti (original work)
The figure above shows a commonly cited relationship between ∆G° and Keq: ∆G° = -RTlnKeq. Here, G° indicates the free energy under standard conditions (e.g., 1 atmosphere of pressure, 298K). In the context of an Energy Story, this equation describes the change in free energy of a reaction whose starting condition is out of equilibrium; specifically, all matter at the "start" is in the form of reactants, and the "end" of the reaction is the equilibrium state. Implicit is the idea that the reaction can theoretically proceed to infinite time so that no matter the shape of its energy surface, it can reach equilibrium. One can also consider a reaction where the "starting" state is somewhere between the starting state above and equilibrium and perhaps where the reaction is not at equilibrium. In this case, one can examine the ∆G (not standard conditions) between the "intermediate" starting state and equilibrium by considering the equation ∆G = ∆G° + RTlnQ, where Q is called the reaction quotient. From the standpoint of BIS2A, we will use a simple (a bit incomplete but functional) definition for Q = [Products]st/[Reactants]st at a defined non-equilibrium "starting" condition st. The equation ∆G = ∆G° + RTlnQ can therefore be read as the free energy of the transformation being equal to the free energy associated with the free energy difference for ideal standard condition plus the contribution of free energy that represents the deviation away from the "ideal" starting state represented by the actual starting state and conditions. In both cases, the "final" condition is still equilibrium; we are just changing starting points. One can extend this idea and calculate the free energy difference between two non-equilibrium states, provided they are properly defined, but that's for your chemistry instructor to bother you with. The key point here is that there is a way to both conceive of and compute free energy changes between specifically defined states, not just the standard initial state and equilibrium as the end state.
This takes us to the core summary point. In many biology books, the discussion of equilibrium includes not only the discussion of forward and reverse reaction rates, but also a statement that ∆G = 0 at equilibrium. This often confuses some students because they are also taught that a nonzero ∆G can be associated with a reaction going to equilibrium. We do this each time we report the ∆G of a reaction or examine a reaction coordinate diagram. So, students tend to memorize the "∆G=0 at equilibrium" statement without appreciating where it comes from. The key to closing the apparent disconnect for many is to appreciate that the interpretation of the sometimes seemingly contradictory statements depend a lot on the definition of the starting and ending states used to calculate ∆G. In the case of reporting ∆G for a reaction, the starting state was described in the paragraphs above (in one of two ways—either standard conditions or non-standard, out-of-equilbrium state), and the ending state is some time later, once the reaction has reached equilibrium. Since the starting and ending states are different, ∆G can be nonzero, positive, or negative. By contrast, the statement that concludes "∆G=0 at equilibrium" is considering a different starting state. In this case, the starting state is the system already at equilibrium. The ending state is considered to be sometime later, but still at equilibrium. Since the starting and ending states are ostensibly the same, ∆G = 0.
Buffers
Since changes in pH can dramatically influence the function of many biomolecules, unicellular and multicellular organisms have developed various means of protecting themselves against changes in pH. One of these mechanisms is the use of small molecules that can, based on their chemical properties, be classified as buffers. Buffers are typically small molecules that can reversibly bind and unbind protons in solution. If the pH in an environment is lower than the pKa of a protonatable functional group on the buffer molecule, that group will tend to become protonated and therefore "remove" a proton from solution. Alternatively, if the pH in an environment is higher than the pKa of the same protonatable functional group on the buffer molecule, that group will tend to become or stay deprotonated, lowering the local pH.
of the body carefully maintained in the narrow range required for survival. Maintaining a constant blood pH is critical to a person’s well-being. The buffer maintaining the pH of human blood involves carbonic acid (H2CO3), bicarbonate ion (HCO3–), and carbon dioxide (CO2). When bicarbonate ions combine with free hydrogen ions and become carbonic acid, hydrogen ions are removed, moderating pH changes. Similarly, excess carbonic acid can be converted to carbon dioxide gas and exhaled through the lungs. This prevents too many free hydrogen ions from building up in the blood and dangerously reducing its pH. Likewise, if too much OH– is introduced into the system, carbonic acid will react with it to create bicarbonate, lowering the pH. Without this buffer system, the body’s pH would fluctuate enough to put survival in jeopardy.
Figure 1. This diagram shows the body’s buffering of blood pH levels. The blue arrows show the process of raising pH as more CO2 is made.
Other examples of buffers are antacids used to combat excess stomach acid. Many of these over-the-counter medications work in the same way as blood buffers, usually with at least one ion capable of absorbing hydrogen and moderating pH, bringing relief to those that suffer from “heartburn” after eating. In addition to the many beneficial characteristics of water, its unique properties that contribute to this capacity to balance pH are essential to sustaining life on Earth.
Functional groups
A functional group is a specific group of atoms within a molecule that is responsible for a characteristic of that molecule. Many biologically active molecules contain one or more functional groups. In BIS2A, we will review the major functional groups found in biological molecules. These include the following: hydroxyl, methyl, carbonyl, carboxyl, amino, and phosphate (see Figure 1).

A functional group may participate in a variety of chemical reactions. Some of the important functional groups in biological molecules are shown above: hydroxyl, methyl, carbonyl, carboxyl, amino, phosphate, and sulfhydryl (not shown). These groups play an important role in the formation of molecules like DNA, proteins, carbohydrates, and lipids. Functional groups can sometimes be classified as having polar or nonpolar properties depending on their atomic composition and organization. The term polar describes something that has a property that is not symmetric about it—it can have different poles (more or less of something at different places). In the case of bonds and molecules, the property we care about is usually the distribution of electrons and therefore electric charge between the atoms. In a nonpolar bond or molecule, electrons and charge will be relatively evenly distributed. In a polar bond or molecule, electrons will tend to be more concentrated in some areas than others. An example of a nonpolar group is the methane molecule (see discussion in Bond Types Chapter for more detail). Among the polar functional groups is the carboxyl group found in amino acids, some amino acid side chains, and the fatty acids that form triglycerides and phospholipids.
Nonpolar functional groups
Methyl R-CH3
The methyl group is the only nonpolar functional group in our class list above. The methyl group consists of a carbon atom bound to three hydrogen atoms. In this class, we will treat these C-H bonds as effectively nonpolar covalent bonds (more on this in the Bond Types chapter). This means that methyl groups are unable to form hydrogen bonds and will not interact with polar compounds such as water.
The methyl groups highlighted above are found in a variety of biologically relevant compounds. In some cases, the compound can have a methyl group but still be a polar compound overall due to the presence of other functional groups with polar properties (see the discussion on polar functional groups below).
As we learn more about other functional groups, we will add to the list of nonpolar functional groups. Stay alert!
Polar functional groups
Hydroxyl R-OH
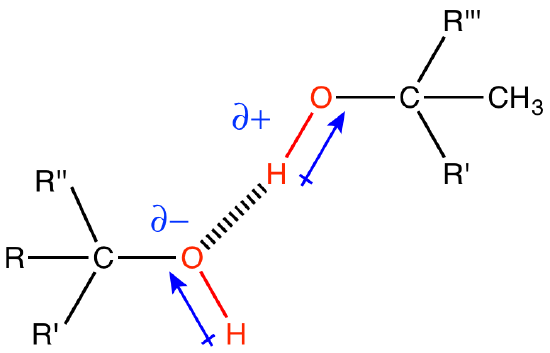
A hydroxyl (alcohol group) is an -OH group covalently bonded to a carbon atom. The oxygen atom is much more electronegative than either the hydrogen or the carbon, which will cause the electrons in the covalent bonds to spend more time around the oxygen than around the C or H. Therefore, the O-H and O-C bonds in the hydroxyl group will be polar covalent bonds. Figure 3 depicts the partial charges, δ+ and δ-, that are associated with the hydroxyl group.
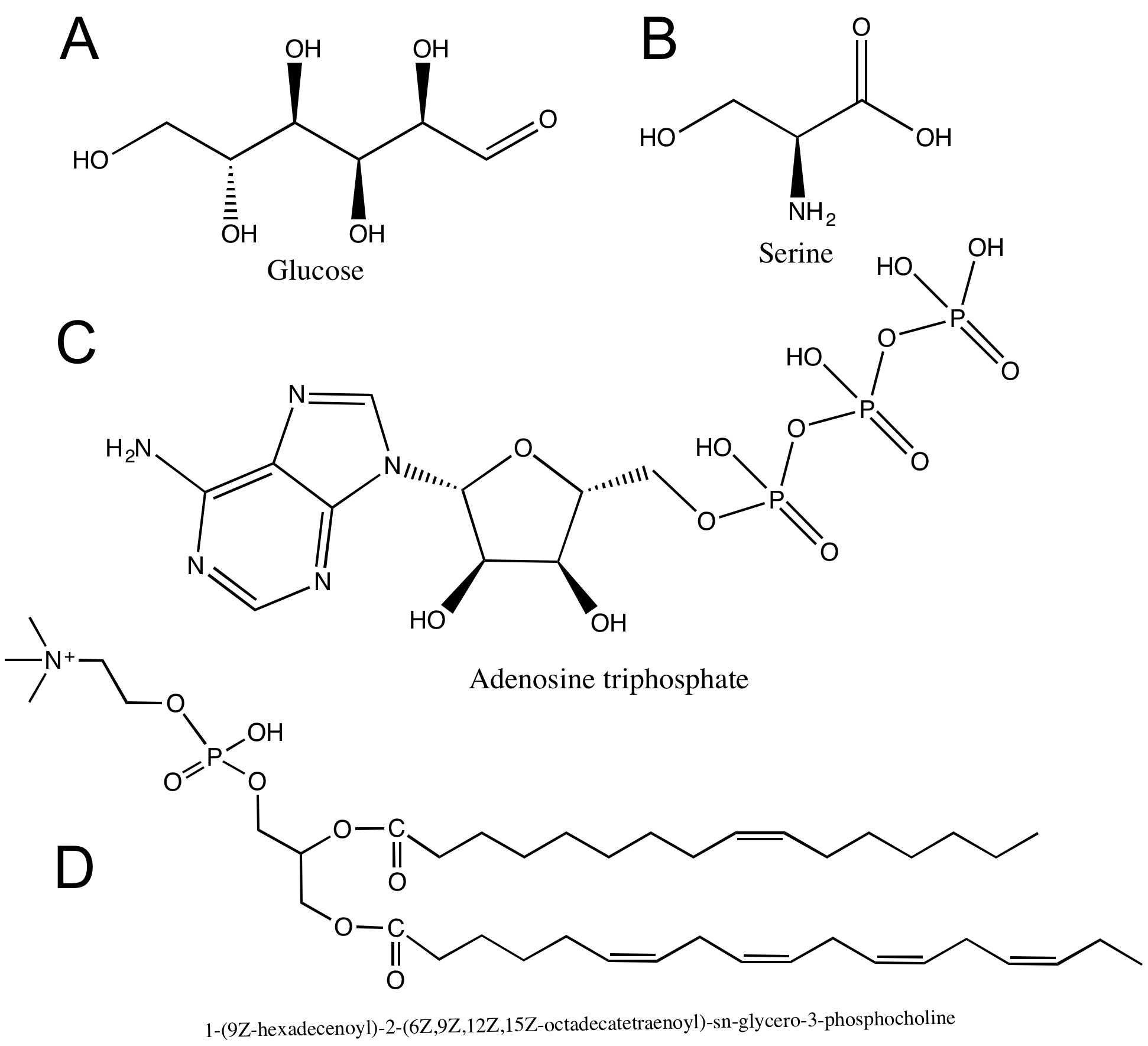
Hydroxyl groups are very common in biological molecules. Hydroxyl groups appear on carbohydrates (A), on some amino acids (B), and on nucleic acids (C). Can you find any hydroxyl groups in the phospholipid in (D)?
Carboxyl R-COOH
Carboxylic acid is a combination of a carbonyl group and a hydroxyl group attached to the same carbon, resulting in new characteristics. The carboxyl group can ionize, which means it can act as an acid and release the hydrogen atom from the hydroxyl group as a free proton (H+). This results in a delocalized negative charge on the remaining oxygen atoms. Carboxyl groups can switch back and forth between protonated (R-COOH) and deprotonated (R-COO-) states depending on the pH of the solution.
The carboxyl group is very versatile. In its protonated state, it can form hydrogen bonds with other polar compounds. In its deprotonated state, it can form ionic bonds with other positively charged compounds. This will have several biological consequences that will be explored more when we discuss enzymes.
Can you identify all the carboxyl groups on the macromolecules shown above in Figure 5?
Amino R-NH3
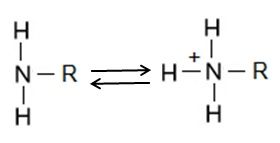
The amino group consists of a nitrogen atom attached by single bonds to hydrogen atoms. An organic compound that contains an amino group is called an amine. Like oxygen, nitrogen is also more electronegative than both carbon and hydrogen, which results in the amino group displaying some polar character.
Amino groups can also act as bases, which means that the nitrogen atom can bond to a fourth hydrogen atom, as shown in Figure 6. Once this occurs, the nitrogen atom gains a positive charge and can now participate in ionic bonds.
Phosphate R-PO4-
A phosphate group is a phosphorus atom covalently bound to four oxygen atoms and contains one P=O bond and three P-O− bonds. The oxygen atoms are more electronegative than the phosphorous atom, resulting in polar covalent bonds. Therefore, these oxygen atoms are able to form hydrogen bonds with nearby hydrogen atoms that also have a δ+(hydrogen atoms bound to another electronegative atom). Phosphate groups also contain a negative charge and can participate in ionic bonds.
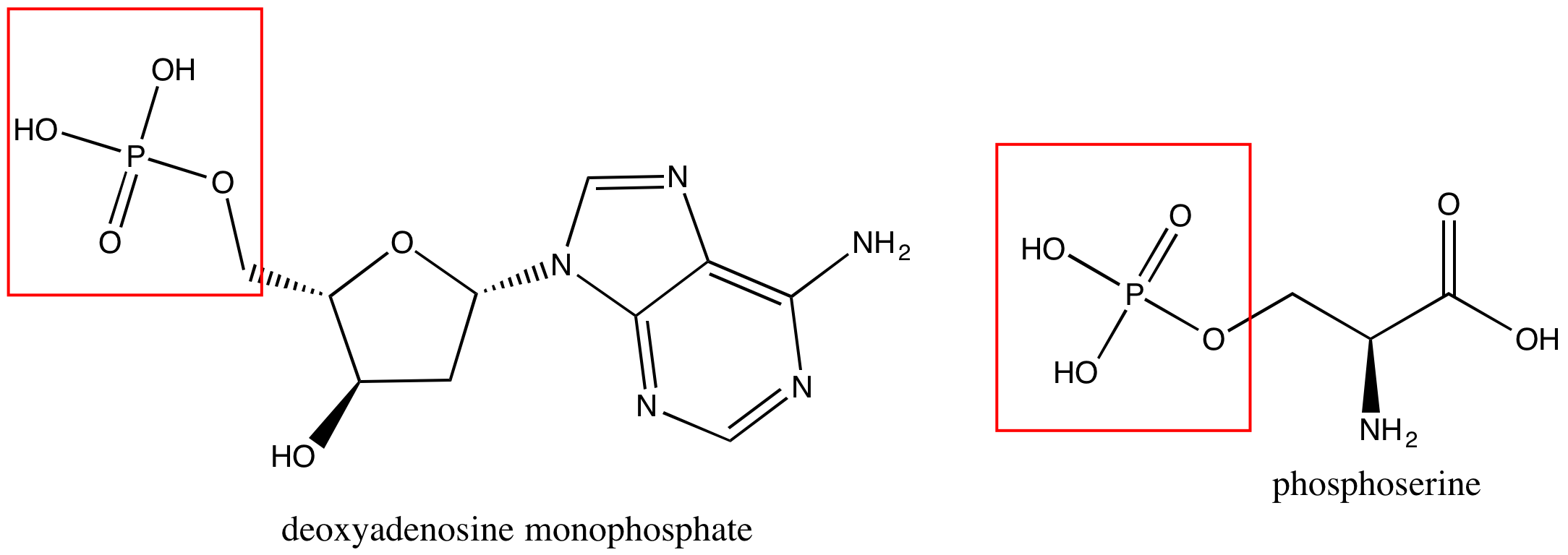
Phosphate groups are common in nucleic acids and on phospholipids (the term "phospho" referring to the phosphate group on the lipid). In Figure 7 are images of a nucleotide, deoxyadenosine monphosphate (left), and a phosphoserine (right).
Figure 7. A nucleotide, deoxyadenosine monphosphate, is on the left, and phosphoserine is on the right. Each has a phosphate group circled in red.
Attribution: created by Marc T. Facciotti (own work)