W2018_Bis2A_Lecture08_reading
- Page ID
- 10596
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Chemical equilibrium—Part 1: forward and reverse reactions
Understanding the concept of chemical equilibrium is critical to following several of the discussions that we have in BIS2A and indeed throughout biology and the sciences. It is difficult to completely describe the concept of chemical equilibrium without reference to the energy of a system, but for the sake of simplicity, let’s try anyway and reserve the discussion of energy for another chapter. Let us, rather, begin developing our understanding of equilibrium by considering the reversible reaction below:

Hypothetical reaction #1: A hypothetical reaction involving compounds A, B and D. If we read this from left to right, we would say that A and B come together to form a larger compound: D. Reading the reaction from right to left, we would say that compound D breaks down into smaller compounds: A and B.
We first need to define what is meant by a “reversible reaction.” The term “reversible” simply means that a reaction can proceed in both directions. That is, the things on the left side of the reaction equation can react together to become the things on the right of the equation, AND the things on the right of the equation can also react together to become the things on the left side of the equation. Reactions that only proceed in one direction are called irreversible reactions.
To start our discussion of equilibrium, we begin by considering a reaction that we posit is readily reversible. In this case, it is the reaction depicted above: the imaginary formation of compound D from compounds A and B. Since it is a reversible reaction, we could also call it the decomposition of D into A and B. Let us, however, imagine an experiment in which we watch the reaction proceed from a starting point where only A and B are present.
Example #1: Left-balanced reaction
| Concentration | t=0 | t=1 | t=5 | t=10 | t=15 | t=20 | t=25 | t=30 | t=35 | t=40 |
|---|---|---|---|---|---|---|---|---|---|---|
| [A] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [B] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [C] | 0 | 10 | 20 | 30 | 45 | 38 | 40 | 40 | 40 | 40 |
At time t = 0 (before the reaction starts), the reaction has 100 concentration units of compounds A and B and zero units of compound D. We now allow the reaction to proceed and observe the individual concentrations of the three compounds over time (t=1, 5, 10, 15, 20, 25, 30, 35, and 40 time units). As A and B react, D forms. In fact, one can see D forming from t=0 all the way to t=25. After that time, however, the concentrations of A, B and D stop changing. Once the reaction reaches the point where the concentrations of the components stop changing, we say that the reaction has reached equilibrium. Notice that the concentrations of A, B, and D are not equal at equilibrium. In fact, the reaction seems left balanced so that there is more A and B than D.
Note
****Common student misconception warning****
Many students fall victim to the misconception that the concentrations of a reaction’s reactants and products must be equal at equilibrium. Given that the term equilibrium sounds a lot like the word “equal,” this is not surprising. But as the experiment above tries to illustrate, this is NOT correct!
Example #2: right-balanced reaction
We can examine a second hypothetical reaction, the synthesis of compound J from the compounds E and F.

Hypothetical reaction #2: A hypothetical reaction involving compounds E, F and J. If we read this from left to right, we would say that E and F come together to form a larger compound: J. Reading the reaction from right to left, we would say that compound J breaks down into smaller compounds: E and F.
The structure of hypothetical reaction #2 looks identical to that of hypothetical reaction #1, which we considered above—two things come together to make one bigger thing. We just need to assume, in this case, that E, F, and J have different properties from A, B, and D. Let’s imagine a similar experiment to the one described above and examine this data:
Hypothetical reaction #2: time course
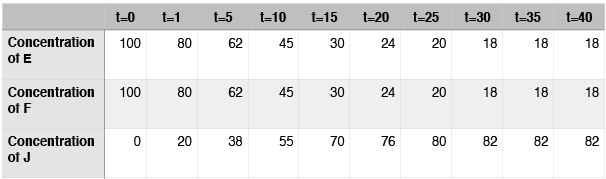
In this case, the reaction also reaches equilibrium. This time, however, equilibrium occurs at around t=30. After that point, the concentrations of E, F, and J do not change. Note again that the concentrations of E, F, and J are not equal at equilibrium. In contrast to hypothetical reaction #1 (the ABD reaction), this time the concentration of J, the thing on the right side of the arrows, is at a higher concentration than E and F. We say that, for this reaction, equilibrium lies to the right.
Four more points need to be made at this juncture.
Point 1: Whether equilibrium for a reaction lies to the left or the right will be a function of the properties of the components of the reaction and the environmental conditions that the reaction is taking place in (e.g., temperature, pressure, etc.).
Point 2: We can also talk about equilibrium using concepts of energy, and we will do this soon, just not yet.
Point 3: While hypothetical reactions #1 and #2 appear to reach a point where the reaction has “stopped,” you should imagine that reactions are still happening even after equilibrium has been reached. At equilibrium the “forward” and “reverse” reactions are just happening at the same rate. That is, in example #2, at equilibrium J is forming from E and F at the same rate that it is breaking down into E and F. This explains how the concentrations of the compounds aren’t changing despite the fact that the reactions are still happening.
Point 4: From this description of equilibrium, we can define something we call the equilibrium constant. Typically, the constant is represented by an uppercase K and may be written as Keq. In terms of concentrations, Keq is written as the mathematical product of the reaction product concentrations (stuff on the right) divided by the mathematical product of the reactant concentrations (stuff on the left). For example, Keq,1 = [D]/[A][B], and Keq,2 = [J]/[E][F]. The square brackets "[]" indicate the “concentration of” whatever is inside the bracket.
Chemical Equilibrium—Part 2: Free Energy
In a previous section, we began a description of chemical equilibrium in the context of forward and reverse rates. Three key ideas were presented:
- At equilibrium, the concentrations of reactants and products in a reversible reaction are not changing in time.
- A reversible reaction at equilibrium is not static—reactants and products continue to interconvert at equilibrium, but the rates of the forward and reverse reactions are the same.
- We were NOT going to fall into a common student trap of assuming that chemical equilibrium means that the concentrations of reactants and products are equal at equilibrium.
Here we extend our discussion and put the concept of equilibrium into the context of free energy, also reinforcing the Energy Story exercise of considering the "Before/Start" and "After/End" states of a reaction (including the inherent passage of time).

Figure 1. Reaction coordinate diagram for a generic exergonic reversible reaction. Equations relating free energy and the equilibrium constant: R = 8.314 J mol-1 K-1 or 0.008314 kJ mol-1 K-1; T is temperature in Kelvin.
Attribution: Marc T. Facciotti (original work)
The figure above shows a commonly cited relationship between ∆G° and Keq: ∆G° = -RTlnKeq. Here, G° indicates the free energy under standard conditions (e.g., 1 atmosphere of pressure, 298K). In the context of an Energy Story, this equation describes the change in free energy of a reaction whose starting condition is out of equilibrium; specifically, all matter at the "start" is in the form of reactants, and the "end" of the reaction is the equilibrium state. Implicit is the idea that the reaction can theoretically proceed to infinite time so that no matter the shape of its energy surface, it can reach equilibrium. One can also consider a reaction where the "starting" state is somewhere between the starting state above and equilibrium and perhaps where the reaction is not at equilibrium. In this case, one can examine the ∆G (not standard conditions) between the "intermediate" starting state and equilibrium by considering the equation ∆G = ∆G° + RTlnQ, where Q is called the reaction quotient. From the standpoint of BIS2A, we will use a simple (a bit incomplete but functional) definition for Q = [Products]st/[Reactants]st at a defined non-equilibrium "starting" condition st. The equation ∆G = ∆G° + RTlnQ can therefore be read as the free energy of the transformation being equal to the free energy associated with the free energy difference for ideal standard condition plus the contribution of free energy that represents the deviation away from the "ideal" starting state represented by the actual starting state and conditions. In both cases, the "final" condition is still equilibrium; we are just changing starting points. One can extend this idea and calculate the free energy difference between two non-equilibrium states, provided they are properly defined, but that's for your chemistry instructor to bother you with. The key point here is that there is a way to both conceive of and compute free energy changes between specifically defined states, not just the standard initial state and equilibrium as the end state.
This takes us to the core summary point. In many biology books, the discussion of equilibrium includes not only the discussion of forward and reverse reaction rates, but also a statement that ∆G = 0 at equilibrium. This often confuses some students because they are also taught that a nonzero ∆G can be associated with a reaction going to equilibrium. We do this each time we report the ∆G of a reaction or examine a reaction coordinate diagram. So, students tend to memorize the "∆G=0 at equilibrium" statement without appreciating where it comes from. The key to closing the apparent disconnect for many is to appreciate that the interpretation of the sometimes seemingly contradictory statements depend a lot on the definition of the starting and ending states used to calculate ∆G. In the case of reporting ∆G for a reaction, the starting state was described in the paragraphs above (in one of two ways—either standard conditions or non-standard, out-of-equilbrium state), and the ending state is some time later, once the reaction has reached equilibrium. Since the starting and ending states are different, ∆G can be nonzero, positive, or negative. By contrast, the statement that concludes "∆G=0 at equilibrium" is considering a different starting state. In this case, the starting state is the system already at equilibrium. The ending state is considered to be sometime later, but still at equilibrium. Since the starting and ending states are ostensibly the same, ∆G = 0.
Catalysts and Enzymes
Catalysts
For a chemical reaction to happen, the reactants must first find one another in space. Chemicals in solution don't "plan" these collisions; they happen at random. In fact, in many cases, it's even more complicated. Not only do the reactants need to run into one another, but they also need to come into contact in a specific orientation. If reactants are very dilute, the rate of the reaction will be slow—collisions will happen infrequently. Increasing the concentrations will increase the rate of productive collisions. Another way to change the rate of reaction is to increase the rate of collisions by increasing the rate at which the reactants explore the reaction space—by increasing the velocity of the molecules or their kinetic energy. This can be accomplished by transferring heat into the system or raising the temperature. Those two strategies are often suitable for increasing the rates of chemical reactions that happen in a tube. However, in the cell, the transfer of heat may not be practical, as it may damage cellular components and lead to death. Cells sometimes use mechanisms to increase concentrations of reactants (we'll see some examples below), but this is rarely enough to drive reaction rates in a biologically relevant regime. This is where catalysts come in.
A catalyst is a something that helps increase the rate of a chemical reaction without undergoing any change itself. You can think of a catalyst as a chemical change agent.
The most important catalysts in biology are called enzymes. An enzyme is a protein catalyst. Other cellular catalysts include molecules called ribozymes. A ribozyme is a catalyst composed of a ribonucleic acid (RNA). Both of these will be discussed in more detail later in the course. Like all catalysts, enzymes work by lowering the level of energy that needs to be transferred into a chemical reaction in order to make it happen. A chemical reaction’s activation energy is the “threshold” level of energy needed to initiate the reaction.
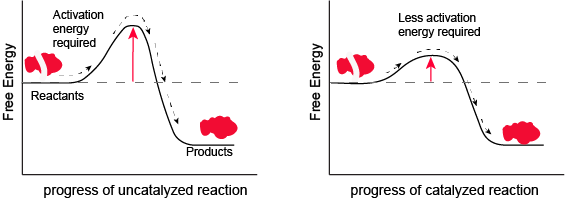
Figure 1. Enzymes and other catalysts decrease the activation energy required to initiate a given chemical reaction. Without an enzyme (left), the energy input needed for a reaction to begin is high. With the help of an enzyme (right), less energy is needed for a reaction to begin.
Attribution: Marc T. Facciotti (original work)
Note: possible discussion
Look at the figure above. What do you think the units are on the x-axis? Time would be one guess. However, if you compare the figures, it appears that the products are formed at the same time whether the activation energy barrier is high or low. Wasn't the point of this figure to illustrate that reactions with high activation energy barriers are slower than those with low activation energy barriers? What's going on?
Enzymes are biological catalysts that accelerate chemical reactions by lowering the activation energy. Enzymes are proteins consisting of one or more polypeptide chains. Enzymes have an active site that provides a unique chemical environment, made up of certain amino acid R groups (residues). This unique environment is well-suited to convert particular chemical reactants for that enzyme, called substrates, into unstable intermediates called transition states. Enzymes and substrates are thought to bind with an induced fit, which means that enzymes and substrates undergo slight conformational adjustments upon substrate contact, leading to binding. Enzymes bind to substrates and catalyze reactions in four different ways: bringing substrates together in an optimal orientation, compromising the bond structures of substrates so that bonds can be more easily broken, providing optimal environmental conditions for a reaction to occur, or participating directly in their chemical reaction by forming transient covalent bonds with the substrates.
Enzyme action must be regulated so that in a given cell at a given time, the desired reactions are being catalyzed and the undesired reactions are not. Enzymes are regulated by cellular conditions, such as temperature and pH. They are also regulated through their location within a cell, sometimes being compartmentalized so that they can only catalyze reactions under certain circumstances. Inhibition and activation of enzymes via other molecules are other important ways that enzymes are regulated. Inhibitors can act competitively, noncompetitively, or allosterically; noncompetitive inhibitors are usually allosteric. Activators can also enhance the function of enzymes allosterically. The most common method by which cells regulate the enzymes in metabolic pathways is through feedback inhibition. During feedback inhibition, the products of a metabolic pathway serve as inhibitors (usually allosteric) of one or more of the enzymes (usually the first committed enzyme of the pathway) involved in the pathway that produces them.
Enzymes
A substance that helps a chemical reaction to occur is a catalyst, and the special molecules that catalyze biochemical reactions are called enzymes. Almost all enzymes are proteins, made up of chains of amino acids, and they perform the critical task of lowering the activation energies of chemical reactions inside the cell. Enzymes do this by binding to the reactant molecules, and holding them in such a way as to make the chemical bond-breaking and bond-forming processes take place more readily. It is important to remember that enzymes don’t change the ∆G of a reaction. In other words, they don’t change whether a reaction is exergonic (spontaneous) or endergonic. This is because they don’t change the free energy of the reactants or products. They only reduce the activation energy required to reach the transition state.
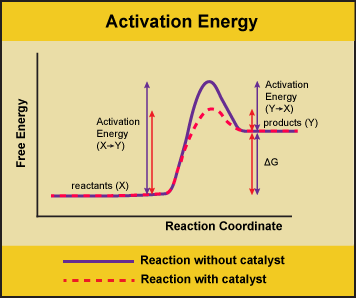
Figure 1: Enzymes lower the activation energy of the reaction but do not change the free energy of the reaction. Here the solid line in the graph shows the energy required for reactants to turn into products without a catalyst. The dotted line shows the energy required using a catalyst. This figure should say Gibbs Free Energy on the Y-axis and instead of noting deltaH should have deltaG. Attribution: Marc T. Facciotti (own work)
Enzyme Active Site and Substrate Specificity
The chemical reactants to which an enzyme binds are the enzyme’s substrates. There may be one or more substrates, depending on the particular chemical reaction. In some reactions, a single-reactant substrate is broken down into multiple products. In others, two substrates may come together to create one larger molecule. Two reactants might also enter a reaction, both become modified, and leave the reaction as two products. The location within the enzyme where the substrate binds is called the enzyme’s active site. The active site is where the “action” happens, so to speak. Since enzymes are proteins, there is a unique combination of amino acid residues (also called side chains, or R groups) within the active site. Each amino acid side-chain is characterized by different properties. Amino acids can be classified as large or small, weakly acidic or basic, hydrophilic or hydrophobic, positively or negatively charged, or neutral. The unique combination of amino acids, their positions, sequences, structures, and properties, creates a very specific chemical environment within the active site. This specific environment is suited to bind, albeit briefly, to a specific chemical substrate (or substrates). Due to this jigsaw puzzle-like match between an enzyme and its substrates (which adapts to find the best fit between the transition state and the active site), enzymes are known for their specificity. The “best fit” between an enzyme and its substrates results from the their respective shapes and the chemical complementarity of the functional groups on each binding partner.
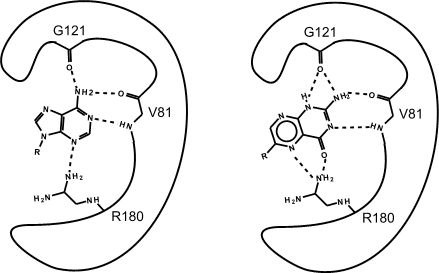
Figure 2: This is an enzyme with two different substrates bound in the active site. The enzymes are represented as blobs, except for the active site which shows the three R-groups of each of the three amino acids located in the active site. These R groups are interacting with the substrates through hydrogen bonding (represented as dashed lines)
At this point in the class you should be familiar with all the types of bonds as well as the chemical characteristics of all the functional groups. For example, the R group of R180 in the enzyme depicted above is the amino acid Arginine (abbreviated as R) and has an R group that consists of several amino functional groups. Amino functional groups contain a nitrogen (N) and hydrogen (H) atoms. Nitrogen is more electronegative than hydrogen so the covalent bond between N-H is a polar covalent bond. The hydrogen atoms in this bond will have a positive dipole moment, and the nitrogen atom will have a negative dipole moment. This allows amino groups to form hydrogen bonds with other polar compounds. Likewise, the backbone carbonyl oxygens of Valine (V) 81 and Glycine (G) 121 the backbone amino hydrogen of V81 are depicted engaged in hydrogen bonds with the small molecule substrate.
Prepare for the Test
Look to see which atoms in the figure above are involved in the hydrogen bonds between the amino acid R groups and the substrate. You will need to be able to identify these on your own, hydrogen bonds may not be drawn in for you on the test.
If you changed the pH of the solution that this enzyme was located in, would the enzyme still be able to form hydrogen bonds with the substrate ?
Which substrate (the left or right one) do you think is more stable in the active site? Why? How?
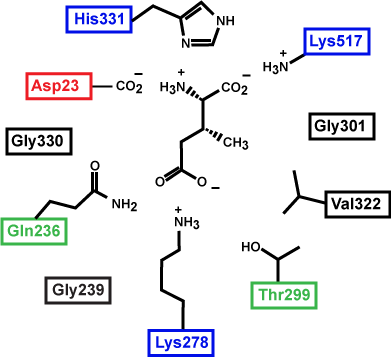
Figure 3: This is an enzyme active site. Only the amino acids in the active site are drawn. The substrate is sitting directly in the center. Source: Created by Marc T. Facciotti (original work)
Note
Prepare for the test: First, identify the type of macromolecule in the figure above. Second, draw in and label the appropriate interactions between the R groups and the substrate. Explain how these interactions might change if the pH of the solution changed.
Structural Instability of Enzymes
The fact that active sites are so well-suited to provide specific environmental conditions also means that they are subject to influences by the local environment. It is true that increasing the environmental temperature generally increases reaction rates, enzyme-catalyzed or otherwise. However, increasing or decreasing the temperature outside of an optimal range can affect chemical bonds within the active site in such a way that they are less well suited to bind substrates. High temperatures will eventually cause enzymes, like other biological molecules, to denature, a process that changes the natural properties of a substance. Likewise, the pH of the local environment can also affect enzyme function. Active site amino acid residues have their own acidic or basic properties that are optimal for catalysis. These residues are sensitive to changes in pH that can impair the way substrate molecules bind. Enzymes are suited to function best within a certain pH range, and, as with temperature, extreme pH values (acidic or basic) of the environment can cause enzymes to denature.
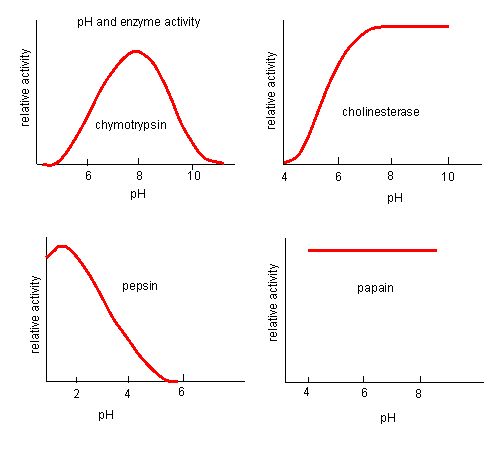
Figure 4: Enzymes have an optimal pH. The pH at which the enzyme is most active will be the pH where the active site R groups are protonated/deprotonated such that the substrate can enter the active site and the initial step in the reaction can begin. Some enzymes require a very low pH (acidic) to be completely active. In the human body, these enzymes are most likely located in the lower stomach, or located in lysosomes (a cellular organelle used to digest large compounds inside the cell). Source: http://biowiki.ucdavis.edu/Biochemis..._pH_Inhibition
The process where enzymes denature usually starts with the unwinding of the tertiary structure through destabilization of the bonds holding the tertiary structure together. Hydrogen bonds, ionic bonds and covalent bonds (disulfide bridges and peptide bonds) can all be disrupted by large changes in temperate and pH. Using the chart of enzyme activity and temperature below, make an energy story for the red enzyme. Explain what might be happening from temperature 37C to 95C.
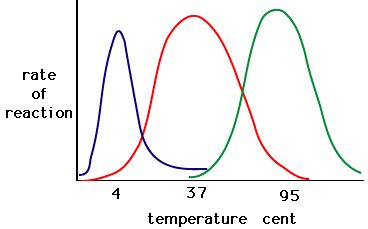
Figure 5: Enzymes have an optimal temperature. The temperature at which the enzyme is most active will usually be the temperature where the structure of the enzyme is stable or uncompromised. Some enzymes require a specific temperature to remain active and not denature. Source: http://academic.brooklyn.cuny.edu/bi...ge/enz_act.htm
Induced Fit and Enzyme Function
For many years, scientists thought that enzyme-substrate binding took place in a simple “lock-and-key” fashion. This model asserted that the enzyme and substrate fit together perfectly in one instantaneous step. However, current research supports a more refined view called induced fit. The induced-fit model expands upon the lock-and-key model by describing a more dynamic interaction between enzyme and substrate. As the enzyme and substrate come together, their interaction causes a mild shift in the enzyme’s structure that confirms an more productive binding arrangement between the enzyme and the transition state of the substrate. This energetically favorable binding maximizes the enzyme’s ability to catalyze its reaction.
When an enzyme binds its substrate, an enzyme-substrate complex is formed. This complex lowers the activation energy of the reaction and promotes its rapid progression in one of many ways. On a basic level, enzymes promote chemical reactions that involve more than one substrate by bringing the substrates together in an optimal orientation. The appropriate region (atoms and bonds) of one molecule is juxtaposed to the appropriate region of the other molecule with which it must react. Another way in which enzymes promote the reaction of their substrates is by creating an energetically favorable environment within the active site for the reaction to occur. Certain chemical reactions might proceed best in a slightly acidic or non-polar environment. The chemical properties that emerge from the particular arrangement of amino acid residues within an active site create the energetically favorable environment for an enzyme’s specific substrates to react.
The activation energy required for many reactions includes the energy involved in slightly contorting chemical bonds so that they can more easily react. Enzymatic action can aid this process. The enzyme-substrate complex can lower the activation energy by contorting substrate molecules in such a way as to facilitate bond-breaking. Finally, enzymes can also lower activation energies by taking part in the chemical reaction itself. The amino acid residues can provide certain ions or chemical groups that actually form covalent bonds with substrate molecules as a necessary step of the reaction process. In these cases, it is important to remember that the enzyme will always return to its original state at the completion of the reaction. One of the hallmark properties of enzymes is that they remain ultimately unchanged by the reactions they catalyze. After an enzyme is done catalyzing a reaction, it releases its product(s).
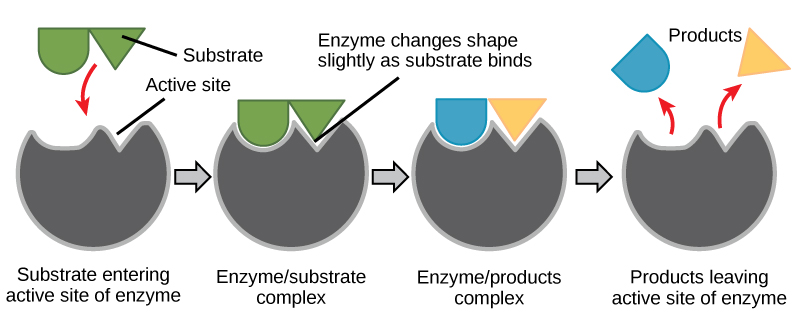
Figure 6: According to the induced-fit model, both enzyme and substrate undergo dynamic conformational changes upon binding. The enzyme contorts the substrate into its transition state, thereby increasing the rate of the reaction.
Creating an Energy story for the reaction above
Using the figure above, answer the questions posed in the energy story.
1. What are the reactants? What are the products?
2. What work was accomplished by the enzyme?
3. What state is the energy in initially? What state is the energy transformed into in the final state? This one might be tricky still, but try to identify where the energy is in the initial state and the final state.
Enzyme Regulation
Why regulate enzymes?
Cellular needs and conditions vary from cell to cell, and change within individual cells over time. The required enzymes and energetic demands of stomach cells are different from those of fat storage cells, skin cells, blood cells, and nerve cells. Furthermore, a digestive cell works much harder to process and break down nutrients during the time that closely follows a meal compared with many hours after a meal. As these cellular demands and conditions vary, so do the needed amounts and functionality of different enzymes.
Regulation of Enzymes by Molecules
Enzymes can be regulated in ways that either promote or reduce their activity. There are many different kinds of molecules that inhibit or promote enzyme function, and various mechanisms exist for doing so. In some cases of enzyme inhibition, for example, an inhibitor molecule is similar enough to a substrate that it can bind to the active site and simply block the substrate from binding. When this happens, the enzyme is inhibited through competitive inhibition, because an inhibitor molecule competes with the substrate for active site binding. On the other hand, in noncompetitive inhibition, an inhibitor molecule binds to the enzyme in a location other than an allosteric site and still manages to block substrate binding to the active site.
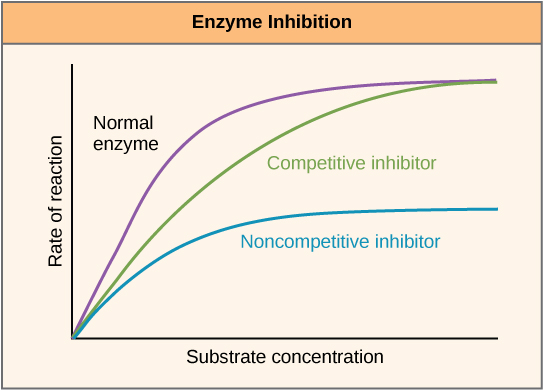
Figure 7: Competitive and noncompetitive inhibition affect the rate of reaction differently. Competitive inhibitors affect the initial rate but do not affect the maximal rate, whereas noncompetitive inhibitors affect the maximal rate.
Some inhibitor molecules bind to enzymes in a location where their binding induces a conformational change that reduces the affinity of the enzyme for its substrate. This type of inhibition is called allosteric inhibition. Most allosterically regulated enzymes are made up of more than one polypeptide, meaning that they have more than one protein subunit. When an allosteric inhibitor binds to an enzyme, all active sites on the protein subunits are changed slightly such that they bind their substrates with less efficiency. There are allosteric activators as well as inhibitors. Allosteric activators bind to locations on an enzyme away from the active site, inducing a conformational change that increases the affinity of the enzyme’s active site(s) for its substrate(s).
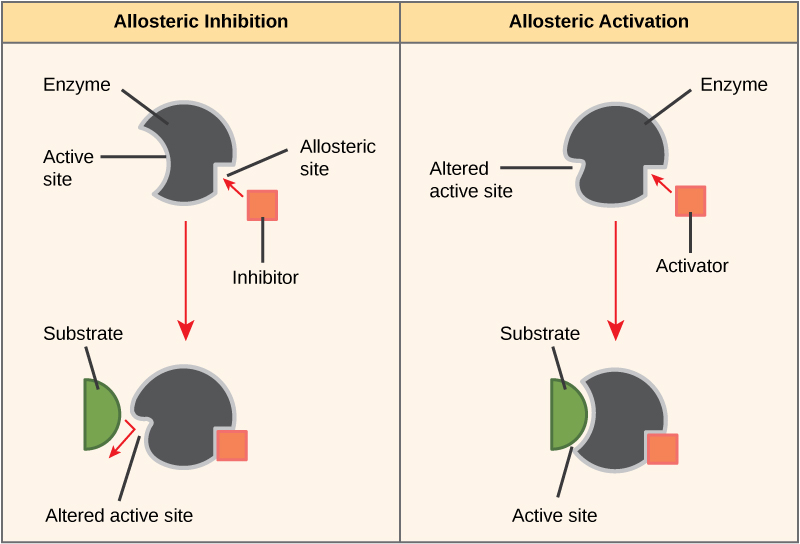
Figure 8: Allosteric inhibitors modify the active site of the enzyme so that substrate binding is reduced or prevented. In contrast, allosteric activators modify the active site of the enzyme so that the affinity for the substrate increases.
Video Link
Check out this short (1 minute) video on competitive vs. noncompetitive enzymatic inhibition. Also, take a look at this video (1.2 minutes) on feed back inhibition.
Many enzymes don’t work optimally, or even at all, unless bound to other specific non-protein helper molecules, either temporarily through ionic or hydrogen bonds or permanently through stronger covalent bonds. Two types of helper molecules are cofactors and coenzymes. Binding to these molecules promotes optimal conformation and function for their respective enzymes. Cofactors are inorganic ions such as iron (Fe2+) and magnesium (Mg2+). One example of an enzyme that requires a metal ion as a cofactor is the enzyme that builds DNA molecules, DNA polymerase, which requires bound zinc ion (Zn2+) to function. Coenzymes are organic helper molecules, with a basic atomic structure made up of carbon and hydrogen, which are required for enzyme action. The most common sources of coenzymes are dietary vitamins. Some vitamins are precursors to coenzymes and others act directly as coenzymes. Vitamin C is a coenzyme for multiple enzymes that take part in building the important connective tissue component, collagen. An important step in the breakdown of glucose to yield energy is catalysis by a multi-enzyme complex called pyruvate dehydrogenase. Pyruvate dehydrogenase is a complex of several enzymes that actually requires one cofactor (a magnesium ion) and five different organic coenzymes to catalyze its specific chemical reaction. Therefore, enzyme function is, in part, regulated by an abundance of various cofactors and coenzymes, which are supplied primarily by the diets of most organisms.
Enzyme Compartmentalization
In eukaryotic cells, molecules such as enzymes are usually compartmentalized into different organelles. This allows for yet another level of regulation of enzyme activity. Enzymes required only for certain cellular processes can be housed separately along with their substrates, allowing for more efficient chemical reactions. Examples of this sort of enzyme regulation based on location and proximity include the enzymes involved in the latter stages of cellular respiration, which take place exclusively in the mitochondria, and the enzymes involved in the digestion of cellular debris and foreign materials, located within lysosomes.
Additional Links
The following links will take you to a series of videos on kinetics. The first link contains 4 videos on reaction rates and the second link contains 9 videos related to the relationship between reaction rates and concentration. These videos are supplemental and are provided to give you an outside resource to further explore enzyme kinetics.

