BIS 2A Ireland Lecture 5
- Page ID
- 11945
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Matter and Energy in Biology
Matter and Energy
The concepts of matter and energy are essential to all scientific disciplines. Yet, while ubiquitous and fundamental, these concepts are often among the most confounding for students. Take the concept of energy. The term is used in a variety of contexts in everyday life:
- “Can we move the couch tomorrow? I don’t have the energy.”
- “Hey dude! Turn the light off. We need to conserve energy.”
- “This is a great energy drink.”
In some sciences classes, students are told that energy comes in different forms (i.e. kinetic, thermal, electrical, potential, etc.). This can sometimes make it difficult to understand exactly what energy “is”. The concept of energy is also associated with many different equations, each with different variables, but that somehow all seem to end up having units of work. Hold on! Work? I thought we were talking about energy?!
Given all the different contexts and sometimes seemingly contradictory treatments and definitions, it’s easy to understand why these topics seem challenging for many students and in some cases end up turning them off of the topics and even fields that make heavy use of these ideas. While the concepts of matter and energy are most often associated with chemistry and physics, they are nevertheless central ideas in biology and we don’t hide from this in BIS2A. In this respect, our instructional goals are to help students develop a framework that help them use the concepts of matter and energy to:
- successfully describe biological reactions and transformations;
- create models and hypotheses for “how things work” in biology that explicitly include matter and energy and;
- be scientifically correct and transfer these ideas to new problems as well as other disciplines.
While there may be a couple of energy-related equations to learn and use in BIS2A, the main focus of the course will be on the robust development of the concepts of energy and matter and their use in the interpretation of biological phenomena.
Motivation for Learning About Matter and Energy
Discussions about matter and energy make some BIS2A students a little apprehensive. After all, aren’t these topics that belong in chemistry or physics? However, the transformations of matter and energy transfer are not phenomena reserved for the chemists and physicists or even scientists and engineers more generally. Understanding, conceptualizing, and doing some basic accounting of transformations of matter and transfers of energy are fundamental skills regardless of occupation or academic training. The scientist may need more rigorous and systematic descriptions of these transformations than the artist but both make use of these skills at various points of their personal and or professional lives. Take the following examples:
Example 1: Matter and Energy Transformation in Global Warming
Let us for a moment consider a topic that affects us all, global warming. At its core lies a relatively simple model that is based on our understanding of energy in solar radiation, the transfer of this energy with matter on the Earth, and the role and cycling of key carbon containing gases in the Earth's atmosphere. In simple terms, solar energy hits the earth and transfers energy to its surface, heating it. Some of this energy is transferred back into space. However, depending on the concentration of carbon dioxide (and other so-called greenhouse gases) different amounts of this energy may become “trapped” in the Earth’s atmosphere. Too little carbon dioxide and relatively little energy/heat is trapped - the Earth freezes and becomes inhospitable for life. Too much carbon dioxide and too much heat is trapped - the Earth overheats and becomes inhospitable for life. It stands to reason, therefore, that mechanisms (biological or other) that influence the levels of carbon dioxide in the atmosphere may be important to consider in the story of global warming and that developing a good understanding of global warming phenomena requires one to trace the flow of the carbon and oxygen (matter) through their different forms and the mechanisms by which energy is transferred to and from different components of the system.
Example 2: Muscle Contraction
Let us now consider a more personal example, the flexing of an arm starting from an extended position and ending in a flexed position. Like most processes, this one can be described and understood at various levels of detail: from the anatomical point of view where the system consists of muscles, skin, and bones to the molecular point of view where the system is composed of individual interacting biomolecules. At whatever level of detail, if we want to create a story describing this process we know that: (a) the description must include an accounting for what happened to the matter in the system (this includes the change in position of the molecules making up the various parts of the arm and the fuel “burned” to move it) and (b) that some fuel was burned to initiate the movement and therefore, that any description of the process must also include an accounting change in the energy of the system. In simpler terms, this is really just saying that if you want to describe a process where something has happened, you need to describe what happened to the “stuff” in the system and what happened to the energy in the system to make the process happen.
We can't possibly cover all examples of matter and energy transfer in BIS2A. But, we will explore these issues often and practice describing transformations that happen in Nature with a structured and explicit attention to what is happening to the matter and energy in a system as it changes. We will do this exercise across different structural levels in biology, from the molecular level (like a single chemical reaction) to more large-scale and abstracted models like nutrient cycling in the environment. We will practice this skill by using a pedagogical tool we call “The Energy Story”. Be prepared to participate!
The energy story
Overview of the energy story
Whether we know it or not, we tell stories that involve matter and energy everyday. We just don’t often use terminology associated with scientific discussions of matter and energy.
Example 1
The setup: a simple statement with implicit details
You tell your roommate a story about how you got to campus by saying, "I biked to campus today." In this simple statement are several assumptions that are instructive to unpack, even if they may not seem very critical to include explicitly in a casual conversation between friends over transportation choices.
An outsider's reinterpretation of the process
To illustrate this, imagine an external observer, such as an alien being watching the comings and goings of humans on Earth. Without the benefit of knowing much of the implied meanings and reasonable assumptions that are buried in our language, the alien's description of the morning cycling trip would be quite different than your own. What you described efficiently as "biking to campus" might be more specifically described by the alien as a change in location of a human body and its bicycle from one location (the apartment, termed position A) to a different location (the university, termed position B). The alien might be even more abstract and describe the bike trip as the movement of matter (the human body and its bike) between an initial state (at location A) to a final state (at location B). Furthermore, from the alien's standpoint, what you'd call "biking" might be more specifically described as the use of a two-wheeled tool that couples the transfer of energy from the electric fields in chemical compounds to the acceleration of the two-wheeled, tool-person combo that heats its environment. Finally, buried within the simple statement describing how we got to work is also the tacit understanding that the mass of the body and bike were conserved in the process (with some important caveats we’ll look at in future lectures) and that some energy was transfered around the system and environment to enable the movement of the body from position A to position B.
Note: possible discussion
Details are important. What if you owned a fully electric bike, and the person you were talking with didn’t know that? What important details might this change about the “everyday” story you told that the more detailed description would have cleared up? How would the alien’s story have changed? In what scenarios might these changes be relevant?
As this simple story illustrates, irrespective of many factors, the act of creating a full description of a process includes some accounting of what happened to the matter, what happened to the energy, and almost always some description of a mechanism that describes how changes in matter and energy of a system were brought about.
To practice this skill in BIS2A, we will make use of something we like to call the "Energy Story." You may be asked to tell an "energy story" in class, to practice telling energy stories on your lecture study guides, and to use the concept on your exams. In this section, we focus primarily on introducing the concept of an energy story and explaining how to tell one. It is worth noting that the term "energy story" is used almost exclusively in BIS2A (and has a specific meaning in this class). This precise term will not appear in other courses at UC Davis (at least in the short term), or if it appears, is not likely to be used in the same manner. You can think of “The Energy Story” as a systematic approach to creating a statement or story describing a biological process or event. Your BIS2A instructors have given this approach a short name (energy story) so that we can all associate it with the common exercise. That way, when the instructor asks the class to tell or construct an energy story, everyone knows what is meant.
Definition 1: energy story
An energy story is a narrative describing a process or event. The critical elements of this narrative are as follows:
- Identify at least two states (e.g., start and end) in the process.
- Identify and list the matter in the system and its state at the start and end of the process.
- Describe the transformation of the matter that occurs during the process.
- Account for the “location” of energy in the system at the start and end of the process.
- Describe the transfer of energy that happens during the process.
- Identify and describe mechanism(s) responsible for mediating the transformation of matter and transfer of energy.
A complete energy story will include a description of the initial reactants and their energetic states as well as a description of the final products and their energetic states after the process or reaction is completed.
Note: possible discussion
We argue that the energy story can be used to communicate all of the useful details that are required to describe nearly any process. Can you think of a process that cannot be adequately described by an energy story? If so, describe such a process.
Example 2: energy story example
Let us suppose that we are talking about the process of driving a car from "Point A" to "Point B" (see Figure 1).
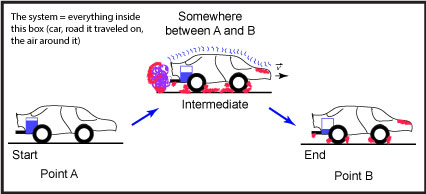
Figure 1: This is a schematic of a car moving from a starting position, "Point A," to an end point, "Point B." The blue rectangle depicted in the back of the car represents the level of the gasoline; the purple, squiggly line near the exhaust pipe represents the exhaust; squiggly blue lines on top of the car represent sound vibrations; and the red shading represents areas that are hotter than at the start. Source: created by Marc T. Facciotti (own work)
Let's step through the Energy Story rubric:
1. Identify at least two states (e.g., start and end) in the process.
In this example, we can easily identify two states. The first state is the nonmoving car at "Point A," the start of the trip. The second state, after the process is done, is the nonmoving car at "Point B."
2. Identify and list the matter in the system and its state at the start and end of the process.
In this case, we first note that the "system" includes everything in the figure—the car, the road, the air around the car, etc.
It is important to understand the we are going to apply the physical law of conservation of matter. That is, in any of the processes that we will discuss, matter is neither created or destroyed. It might change form, but one should be able to account for everything at the end of a process that was there at the beginning.
At the beginning of the process, the matter in the system consists of the following:
1. The car and all the stuff in it
2. The fuel in the car (a special thing in the car)
3. The air (including oxygen) around the car.
4. The road
5. The driver
At the end of the process, the matter in the system is distributed as follows:
1. The car and all the stuff in it is in a new place (let's assume, aside from the fuel and position, that nothing else changed).
2. There is less fuel in the car, and it too is in a new place.
3. The air has changed; it now has less molecular oxygen, more carbon dioxide, and more water vapor.
4. The road did not change (let's assume it didn't change—other than a few pebbles that moved around).
5. The driver did not change (let's assume she didn't change—though we'll see by the end of the term that she did, at least a little). However, the driver is now in a different place.
3. Describe the transformation of the matter that occurs during the process.
What happened to the matter in this process? Thanks to a lot of simplifying assumptions, we see that two big things happened. First, the car and its driver changed positions—they went from "Point A" to "Point B." Second, we note that some of the molecules in the fuel, which used to be in the car as a liquid, have changed forms and are now mostly in the form of carbon dioxide and water vapor (purple blob coming out of the tailpipe). Some of the oxygen molecules that used to be in the air are now also in a new place as part of the carbon dioxide and water that left the car.
4. Account for the “location” of energy in the system at the start and end of the process.
It is again important to understand that we are going to invoke the physical law of conservation of energy. That is, we stipulate that the energy in the system cannot be created or destroyed, and therefore, the energy that is in the system at the start of the process must still be there at the end of the process. It may have been redistributed, but you should be able to account for all the energy.
At the beginning of the process, the energy in the system is distributed as follows:
1. The energy is tied up in the associations between atoms that make up the matter of the car.
2. The energy is tied up in the associations between atoms that make up the fuel.
3. The energy is tied up in the associations between atoms that make up the air.
4. The energy is tied up in the associations between atoms that make up the road.
5. The energy is tied up in the associations between atoms that make up the driver.
6. For all the things above, we can also say that there is energy in the molecular motions of the atoms that make up the stuff.
At the end of the process, the energy in the system is distributed as follows:
1. The energy is tied up in the associations between atoms that make up the matter of the car.
2. The energy is tied up in the associations between atoms that make up the fuel.
3. The energy is tied up in the associations between atoms that make up the air.
4. The energy is tied up in the associations between atoms that make up the road.
5. The energy is tied up in the associations between atoms that make up the driver.
6. For all the things above, we can also say that there is energy in the molecular motions of the atoms that make up the stuff.
This is interesting in some sense, because the lists are about the same. We know that the amount of energy stored in the car has decreased, because there is less fuel. Something must have happened.
5. Describe the transfer of energy that happens during the process.
In this particular example, it is the transfer of energy among the components of the system that is most interesting. As we mentioned, there is less energy stored in the gas tank of the car at the end of the trip, because there is now less fuel. We also know intuitively (from real-life experience) that the transfer of energy from the fuel to something else was instrumental in moving the car from "Point A" to "Point B." So, where did this energy go? Remember, it didn't just disappear. It must have moved somewhere else in the system.
Well, we know that there is more carbon dioxide and water vapor in the system after the process. There is energy in the associations between those atoms (atoms that used to be in the fuel and air). So some of the energy that was in the fuel is now in the exhaust. Let's also draw from real-life experience again, and state that we know that parts of our car have gotten hot by the end of the trip (e.g., the engine, transmission, wheels/tires, exhaust, etc.). For the moment, we'll just use our intuition, and say that we understand that making something hot involves some transfer of energy. So we can reasonably postulate that some of the energy in the fuel went (directly or indirectly) into heating the car, parts of the road, and the exhaust—and thus the environment around the car. An amount of energy also went into accelerating the car from zero velocity to whatever speed it traveled at, but most of that energy eventually became heat when the car came to a stop.
This is a bit of a hand-wavy explanation, and we'll learn how to do a better job throughout the quarter. The main point is that we should be able to add all the energy of the system at the beginning of the process (in all the places it is found) and at the end of the process (in all the places it is found), and those two values should be the same.
6. Identify and describe mechanism(s) responsible for mediating the transformation of matter and transfer of energy.
Finally, it is useful to try understanding how those transformations of matter and transfers of energy might have been facilitated. For the sake of brevity, we might just say that there was a complicated mechanical device (the engine) that helped facilitate the conversion of matter and transfer of energy about the system and coupled this to the change in position of the car. Someone interested in engines would, of course, give a more detailed explanation.
In this example, we made a bunch of simplifying assumptions to highlight the process and to focus on the transformation of the fuel. But that's fine. The more you understand about the processes, the finer details you can add. Note that you can use the Energy Story rubric for describing your understanding (or looking for holes in your understanding) of nearly any process (certainly in biology). In BIS2A, we'll use the Energy Story to get an understanding of processes as varied as biochemical reactions, DNA replication, the function of molecular motors, etc.
Important:
First: We will be working on many examples of the energy story throughout the course—do not feel that you need to have mastery over this topic today.
Second: While it is tempting to think all this is superfluous or not germane to your study of biology in BIS2A, let this serve as a reminder that your instructors (those creating the course midterm and final assessments) view it as core material. We will revisit this topic often throughout the course but need you to get familiar with some of the basic concepts now.
This is important material and an important skill to develop—do not put off studying it because it doesn't "look" like "biology" to you today. The academic term moves VERY quickly, and it will be difficult to catch up later if you don't give this some thought now.
Thermodynamics
Thermodynamics is concerned with describing the changes in systems before and after a change. This usually involves a discussion about energy transfers and its dispersion within the system and its surroundings. In nearly all practical cases, these analyses require that the system and its surroundings be completely described. For instance, when discussing the heating of a pot of water on the stove, the system may includes the stove, the pot, and the water and the environment or surroundings may include everything else. Biological organisms are what are called open systems; energy is transferred between them and their surroundings.
The First Law of Thermodynamics
The first law of thermodynamics deals with the total amount of energy in the universe. It states that this total amount of energy is constant. In other words, there always has been, and always will be, exactly the same amount of energy in the universe.
According to the first law of thermodynamics, energy may be transferred from place to place, but it cannot be created or destroyed. Energy transfers take place around us all the time. Light bulbs transfer energy from electrical power stations into heat and photons of light. Gas stoves transfer energy stored in the bonds of chemical compounds into heat and light. (Heat, by the way, is the amount of energy transferred from one system to another because of a temperature difference.)
Plants perform one of the most biologically useful energy transfers on earth: they transfer energy in the photons of sunlight into the chemical bonds of organic molecules. In every one of these cases, energy is neither made nor destroyed, and we must try to account for all of the energy when we examine some of these reactions.
The First Law and the Energy Story
The first law of thermodynamics is deceptively simple. Students often understand that energy cannot be created or destroyed. Yet, when describing an energy story of a process they often make the mistake of saying things such as "energy is produced from the transfer of electrons from atom A to atom B." While most of us will understand the point the student is trying to make, the wrong words are being used. Energy is not made or produced; it is simply transferred. To be consistent with the first law, when telling an energy story, make sure that you try to explicitly track all of the places that ALL of the energy in the system at the start of a process goes by the end of a process.
The Second Law of Thermodynamics
An important concept in physical systems is that of entropy. Entropy is related to the ways in which energy can be distributed or dispersed within the particles of a system. The Second Law of Thermodynamics states that entropy is always increasing in a system and its surroundings (that is, everything outside the system).
This idea helps explain the directionality of natural phenomena. In general, the notion is that the directionality comes from the tendency for energy in a system to move towards a state of maximal dispersion. The Second Law, therefore, implies that in any transformation, we should look for an overall increase in entropy (or dispersion of energy), somewhere. As dispersion of energy in a system or its surroundings increases, the ability of the energy to be directed towards work decreases.
Keep in mind: you will find many examples in which the entropy of a system decreases locally. However, according to the Second Law, the entropy of the entire universe can never decrease. This must mean that there is an equal or greater increase in entropy somewhere else in the surroundings (most likely in a closely-connected system) that compensates for the local decrease.
Exercise
The entropy of a system can increase when:
- the system gains energy;
- a change of state occurs from solid to liquid to gas;
- a mixing of substances occurs;
- the number of particles increases during a reaction.
possible discussion
Does the second law say that entropy is conserved?
possible discussion
Biological systems, on the surface, seem to defy the Second Law of Thermodynamics. They don't. Why?
Figure 1. An increase in disorder can happen in different ways. An ice cube melting on a hot sidewalk is one example. Here, ice is displayed as a snowflake, with organized, structured water molecules forming the snowflake. Over time, the snowflake will melt into a pool of disorganized, freely moving water molecules. (Source)
possible discussion
A fine point. Figure 1 above discusses order and disorder and shows that this is somehow related to a change in entropy (ΔS). It is common to describe entropy as a measure of order as a way to simplify the more concrete description relating entropy to the number of states in which energy can be dispersed in a system. While the idea of measuring order to define entropy has some flaws, it is sometimes a useful, if imperfect, proxy. Consider the figure above. Here, order serves as a good proxy for approximating the number of ways to distribute energy in the system. Can you describe why this is the case?
If we consider the first and second laws together, we come to a useful conclusion. Whenever energy is transferred or redistributed within a system, entropy must increase. This increase in entropy is related to how "useful" the energy is to do work. Recall again that this energy generally becomes less and less available as entropy increases.
We conclude that while all of the energy must be conserved, if the required change increases entropy, it means that some of the energy will become distributed in a way that makes it less useful for work. In many cases, particularly in biology, some of the increase in entropy can be chalked up to a transfer of energy to heat in the environment.
Energy in chemical reactions
Chemical reactions involve a redistribution of energy within the reacting chemicals and with their environment. So, like it or not, we need to develop some models that can help us to describe where energy is in a system (perhaps how it is "stored"/distributed) and how it can be moved around in a reaction. The models we develop will not be overly detailed in the sense that they would satisfy a hard-core chemist or physicist with their level of technical detail, but we expect that they should still be technically correct and not form incorrect mental models that will make it difficult to understand the "refinements" later.
In this respect, one of the key concepts to understand is that we are going to think about energy being transferred between parts of a system rather than referring thinking too much about it as being transformed. The distinction between "transfer" and "transform" is important because the latter gives the impression that energy is a property that exists in different forms, that it gets reshaped somehow. The common use of the term "transform" in relation to energy is understandable as different phenomena associated with the concept of energy physically "look" different to us. However, one potential problem with using the "transform" language is that it is sometimes difficult to reconcile with the idea that energy is being conserved (according to the first law of thermodynamics) if it is constantly changing form. How can the entity of energy be conserved if after a transformation it is no longer the same thing (e.g. transformed)? Moreover, the second law of thermodynamics tells us that no transformation conserves all energy in a system. If energy is getting "transformed," how can it be conserved and still be consistent with the second law of thermodynamics?
So, instead, we are going to approach this issue by transferring and storing energy between different parts of a system and thus think about energy as a property that can get redistributed. That'll hopefully make the accounting of energy easier. Not that the energy "transfer" idea is, of course, completely consistent and compatible with terms like "potential energy" and "kinetic energy", as these are useful for describing how the energy is distributed between the motion of matter and the various fields (e.g. electric, gravational, etc.) in a system.
CAUTION
If we are going to think about transferring energy from one part of a system to another, we also need to be careful about NOT treating energy like a substance that moves like a fluid or "thing." Rather, we need to appreciate energy simply as a property of a system that can be measured and reorganized but that is neither a "thing" nor something that is at one time in one form then later in another.
Since we will often be dealing with transformations of biomolecules, we can start by thinking about where energy can be found/stored in these systems. We'll start with a couple of ideas and add more to them later.
Let us propose that one place that energy can be stored is in the motion of matter. For brevity, we'll give the energy stored in motion a name: kinetic energy. Molecules in biology are in constant motion and therefore have a certain amount of kinetic energy (energy stored in motion) associated with them.
Let us also propose that there is a certain amount of energy stored in the biomolecules themselves and that the amount of energy stored in those molecules is associated with the types and numbers of atoms in the molecules and their organization (the number and types of bonds between them). The discussion of exactly where the energy is stored in the molecules is beyond the scope of this class, but we can approximate it by suggesting that a good proxy is in the bonds. Different types of bonds may be associated with storing different amounts of energy. In some contexts, this type of energy storage could be labeled potential energy or chemical energy. With this view, one of the things that happens during the making and breaking of bonds in a chemical reaction is that the energy is transferred about the system into different types of bonds. In the context of an Energy Story, one could theoretically count the amount of energy stored in the bonds and motion of the reactants and the energy stored in the bonds and energy of the products.
In some cases, you might find that when you add up the energy stored in the products and the energy stored in the reactants that these sums are not equal. If the energy in the reactants is greater than that in the products, where did this energy go? It had to get transferred to something else. Some will certainly have moved into other parts of the system, stored in the motion of other molecules (warming the environment) or perhaps in the energy associated with photons of light. One good, real-life example is the chemical reaction between wood and oxygen (reactants) and it's conversion to carbon dioxide and water (products). At the beginning, the energy in the system is largely in the molecular bonds of oxygen and the wood (reactants). There is still energy left in the carbon dioxide and water (products) but less than at the beginning. We all appreciate that some of that energy was transferred to the energy in light and heat. This reaction where energy is transferred to the environment is termed exothermic. By contrast, in some reactions, energy will transfer in from the environment. These reactions are endothermic.
The transfer of energy in or out of the reaction from the environment is NOT the only thing that determines whether a reaction will be spontaneous or not. We'll discuss that soon. For the moment, it is important to get comfortable with the idea that energy can be transferred among different components of a system during a reaction and that you should be able to envision tracking it.
Chemical equilibrium—Part 1: Forward and reverse reactions
Understanding the concept of chemical equilibrium is also critical to following several of the discussions that we have in BIS2A and indeed throughout biology and the sciences. It is difficult to completely describe the concept of chemical equilibrium without reference to the energy of a system, but for the sake of simplicity, let’s try anyway and reserve the discussion of energy for another chapter. Let us, rather, begin developing our understanding of equilibrium by considering the reversible reaction below:

Hypothetical reaction #1: A hypothetical reaction involving compounds A, B and D. If we read this from left to right, we would say that A and B come together to form a larger compound: D. Reading the reaction from right to left, we would say that compound D breaks down into smaller compounds: A and B.
We first need to define what is meant by a “reversible reaction.” The term “reversible” simply means that a reaction can proceed in both directions. That is, the things on the left side of the reaction equation can react together to become the things on the right of the equation, AND the things on the right of the equation can also react together to become the things on the left side of the equation. Reactions that only proceed in one direction are called irreversible reactions.
To start our discussion of equilibrium, we begin by considering a reaction that we posit is readily reversible. In this case, it is the reaction depicted above: the imaginary formation of compound D from compounds A and B. Since it is a reversible reaction, we could also call it the decomposition of D into A and B. Let us, however, imagine an experiment in which we watch the reaction proceed from a starting point where only A and B are present.
Example #1: Left-balanced reaction
| Concentration | t=0 | t=1 | t=5 | t=10 | t=15 | t=20 | t=25 | t=30 | t=35 | t=40 |
|---|---|---|---|---|---|---|---|---|---|---|
| [A] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [B] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [C] | 0 | 10 | 20 | 30 | 45 | 38 | 40 | 40 | 40 | 40 |
At time t = 0 (before the reaction starts), the reaction has 100 concentration units of compounds A and B and zero units of compound D. We now allow the reaction to proceed and observe the individual concentrations of the three compounds over time (t=1, 5, 10, 15, 20, 25, 30, 35, and 40 time units). As A and B react, D forms. In fact, one can see D forming from t=0 all the way to t=25. After that time, however, the concentrations of A, B and D stop changing. Once the reaction reaches the point where the concentrations of the components stop changing, we say that the reaction has reached equilibrium. Notice that the concentrations of A, B, and D are not equal at equilibrium. In fact, the reaction seems left balanced so that there is more A and B than D.
Note: Common student misconception warning
Many students fall victim to the misconception that the concentrations of a reaction’s reactants and products must be equal at equilibrium. Given that the term equilibrium sounds a lot like the word “equal,” this is not surprising. But as the experiment above tries to illustrate, this is NOT correct!
Example #2: right-balanced reaction
We can examine a second hypothetical reaction, the synthesis of compound \(\ce{J}\) from the compounds \(\ce{E}\) and \(\ce{F}\).
\[ \ce{E +F <=> J} \nonumber\]
Hypothetical reaction #2: A hypothetical reaction involving compounds E, F and J. If we read this from left to right, we would say that E and F come together to form a larger compound: J. Reading the reaction from right to left, we would say that compound J breaks down into smaller compounds: E and F.
The structure of hypothetical reaction #2 looks identical to that of hypothetical reaction #1, which we considered above—two things come together to make one bigger thing. We just need to assume, in this case, that E, F, and J have different properties from A, B, and D. Let’s imagine a similar experiment to the one described above and examine this data:
Hypothetical reaction #2: time course
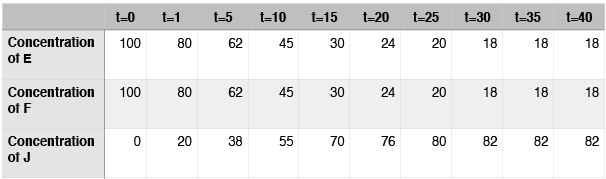
In this case, the reaction also reaches equilibrium. This time, however, equilibrium occurs at around t=30. After that point, the concentrations of E, F, and J do not change. Note again that the concentrations of \(\ce{E}\), \(\ce{F}\), and \(\ce{J}\) are not equal at equilibrium. In contrast to hypothetical reaction #1 (the ABD reaction), this time the concentration of J, the thing on the right side of the arrows, is at a higher concentration than E and F. We say that, for this reaction, equilibrium lies to the right.
Four more points need to be made at this juncture.
- Point 1: Whether equilibrium for a reaction lies to the left or the right will be a function of the properties of the components of the reaction and the environmental conditions that the reaction is taking place in (e.g., temperature, pressure, etc.).
- Point 2: We can also talk about equilibrium using concepts of energy, and we will do this soon, just not yet.
- Point 3: While hypothetical reactions #1 and #2 appear to reach a point where the reaction has “stopped,” you should imagine that reactions are still happening even after equilibrium has been reached. At equilibrium the “forward” and “reverse” reactions are just happening at the same rate. That is, in example #2, at equilibrium J is forming from E and F at the same rate that it is breaking down into E and F. This explains how the concentrations of the compounds aren’t changing despite the fact that the reactions are still happening.
- Point 4: From this description of equilibrium, we can define something we call the equilibrium constant. Typically, the constant is represented by an uppercase K and may be written as Keq. In terms of concentrations, Keq is written as the mathematical product of the reaction product concentrations (stuff on the right) divided by the mathematical product of the reactant concentrations (stuff on the left). For example, Keq,1 = [D]/[A][B], and Keq,2 = [J]/[E][F]. The square brackets "[]" indicate the “concentration of” whatever is inside the bracket.
Free Energy
If we want to describe transformations, it is useful to have a measure of (a) how much energy is in a system, (b) the dispersal of that energy within the system and, of course, (c) how these factors change between the start and end of a process. The concept of free energy, often referred to as Gibbs energy or Gibbs enthalpy (abbreviated with the letter G), in some sense, does just that. Gibbs energy can be defined in several interconvertible ways, but a useful one in the context of biology is the enthalpy (internal energy) of a system minus the entropy of the system scaled by the temperature. The difference in free energy when a process takes place is often reported in terms of the change (Δ) of enthalpy (internal energy) denoted H, minus the temperature scaled change (Δ) in entropy, denoted S. See the equation below.
ΔG=ΔH−TΔS (1)
The Gibbs energy is often interpreted as the amount of energy available to do useful work. With a bit of hand waving, we can interpret this statement by invoking the idea presented in the section on entropy, which states the dispersion of energy (required by the Second Law) associated with a positive change in entropy somehow renders some of the energy that is transferred less useful to do work. One can say that this is reflected in part in the T∆ST∆S term of the Equation 1.
To provide a basis for fair comparisons of changes in Gibbs energy amongst different biological transformations or reactions, the free energy change of a reaction is measured under a set of common standard experimental conditions. The resulting standard free energy change of a chemical reaction is expressed as an amount of energy per mole of the reaction product (either in kilojoules or kilocalories, kJ/mol or kcal/mol; 1 kJ = 0.239 kcal), when measured at a standard pH, temperature, and pressure conditions. Standard pH, temperature, and pressure conditions are generally standardized at pH 7.0, 25 degrees Celsius, and 100 kilopascals (1 atm pressure), respectively.It is important to note that cellular conditions vary considerably from these standard conditions, and so actual ∆G inside a cell will differ considerably from those calculated under standard conditions.
Endergonic and exergonic reactions
Any system of molecules that undergos a physical transformation/reorganizaton (aka. reaction) will have an associated change in internal energy and entropy. If we examine a single isolated reaction, in which unique reactants are converted into unique products the Gibbs energy of the system will be dependent several factors, key among which are (a) the internal energy and entropy differences associated with the molecular rearrangements and (b) the degree to which the reaction is out-of-equilibrium.
If, for the sake of simplicity we begin by considering only the contribution of the molecular transformations in the system on ∆G, we conclude that reactions with ∆G < 0, the products of the reaction have less Gibbs energy than the reactants. Since ∆G is the difference between the enthalpy and temperature-scaled entropy changes in a reaction, a net negative ∆G can arise in through changes largely of enthalpy, entropy or most often both. The left panel of Figure 1 below shows a common graphical representation of an exergonic reaction. This type of graph is called a reaction coordinate diagram. Gibbs energy is plotted on the y-axis, and the x-axis in arbitrary units shows the progress of a reaction. In the case of an exergonic reaction, the figure on the left indicates two key things: (1) the difference between the free energy of the reactants and products is negative and (2) the progress of the reaction requires some input of free energy (shown as an energy "hill" or barrier). This graph does not tell us how the energy in the system was redistributed, only that the difference between enthalpy and temperature-scaled entropy is negative. Exergonic reactions are said to occur spontaneously. Understanding which chemical reactions are spontaneous is extremely useful for biologists who are trying to understand whether a reaction is likely to "go" or not.
It is important to note that the term "spontaneous"—in the context of thermodynamics—does NOT imply anything about how fast the reaction proceeds. The change in free energy only describes the difference between beginning and end states, NOT how fast that transition takes place. This is somewhat contrary to the everyday use of the term, which usually carries the implicit understanding that something happens quickly. As an example, the oxidation/rusting of iron is a spontaneous reaction. However, an iron nail exposed to air does not rust instantly—it may take years.
A chemical reaction with a positive ∆G means that the products of the reaction have a higher free energy than the reactants (see the right panel of Figure 1). These chemical reactions are called endergonic reactions, and they are NOT spontaneous. An endergonic reaction will not take place on its own without the transfer of energy into the reaction or increase of entropy somewhere else.
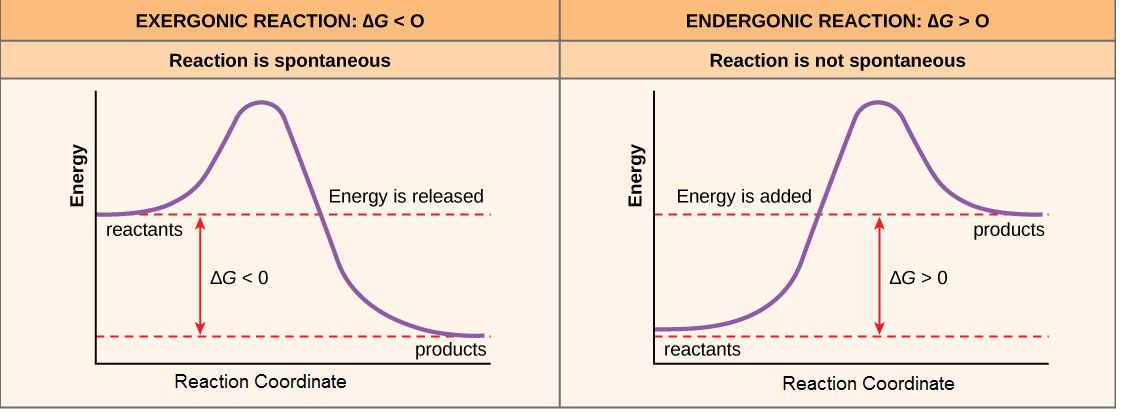
Figure 1. Reaction coordinate diagrams of exergonic and endergonic reactions. Exergonic and endergonic reactions are characterized by changes in Gibbs energy. In the equilibrium state of an exergonic reaction, the Gibbs energy of the products is lower than that of the reactants. Meanwhile, the equilibrium state of an endergonic reaction in, the Gibbs energy of the products is higher than that of the reactants. Attribution: Marc T. Facciotti (own work)
The building of complex molecules, such as sugars, from simpler ones is an anabolic process and is endergonic. On the other hand, the catabolic process, such as the breaking down of sugar into simpler molecules, is generally exergonic. Like the example of rust above, while the breakdown of biomolecules is generally spontaneous, these reactions don’t necessarily occur instantaneously (quickly). Remember, the terms endergonic and exergonic only refer to the difference in Gibbs energy between the products and reactants; they don't tell you about the rate of the reaction (how fast it happens). The issue of rate will be discussed in later sections.
An important concept in the study of metabolism and energy is that of chemical equilibrium. Most chemical reactions are reversible. They can proceed in both directions, often transferring energy into their environment in one direction and transferring energy in from the environment in the other direction. The same is true for the chemical reactions involved in cell metabolism, such as the breaking down and building up of proteins into and from individual amino acids, respectively. Reactants within a closed system will undergo chemical reactions in both directions until a state of equilibrium is reached. Equilibrium in a chemical reaction is the state in which both reactants and products are present in concentrations that have no further tendency to change with time. Usually, this state results when the forward reaction proceeds at the same rate as the reverse reaction. NOTE THIS LAST STATEMENT! Equilibrium means that the relative concentrations of reactants and products are not changing in time, BUT it does NOT mean that there is no interconversion between substrates and products—it just means that when the reactant(s) are converted to product(s) that product(s) are converted to reactant(s) at an equal rate (see Figure 2). The state of equilibrium is also one of the lowest possible free energy states for the reaction and is a state of maximal entropy.
If a reaction is kept or started far out of equilibrium this state of the system also contributes to the overall Gibbs energy of a reaction. Either a rebalancing of substrate or product concentrations (by adding or removing substrate or product) or a positive change in free energy, typically by the transfer of energy from outside the reaction, can to move a reaction to an out-of-equilibrium state. Note that in a living cell, most chemical reactions do not reach a state of equilibrium—this would require that they reach their lowest free energy state, a state that is almost by definition incompatible with life. Energy is therefore required to keep biological reactions out of their equilibrium state. In this way, living organisms are in a constant, energy-requiring, uphill battle against equilibrium and entropy. This also means that the Gibbs energy of most biological reactions as they occur in the cell must also include a contribution from this out-of-equilibrium state. The Gibbs energy of these reactions, therefore, is often different from that reported under standard conditions.

Figure 2. At equilibrium, do not think of a static, unchanging system. Instead, picture molecules moving in equal amounts from one area to another. Here, at equilibrium, molecules are still moving from left to right and right to left. The net movement however, is equal. There will still be about 15 molecules in each side of this flask once equilibrium is reached. Source: https://courses.candelalearning.com/...apter/entropy/
Chemical Equilibrium—Part 2: Gibbs Energy
In a previous section, we began a description of chemical equilibrium in the context of forward and reverse rates. Three key ideas were presented:
- At equilibrium, the concentrations of reactants and products in a reversible reaction are not changing in time.
- A reversible reaction at equilibrium is not static—reactants and products continue to interconvert at equilibrium, but the rates of the forward and reverse reactions are the same.
- We were NOT going to fall into a common student trap of assuming that chemical equilibrium means that the concentrations of reactants and products are equal at equilibrium.
Here we extend our discussion and put the concept of equilibrium into the context of Gibbs energy, also reinforcing the Energy Story exercise of considering the "Before/Start" and "After/End" states of a reaction (including the inherent passage of time).
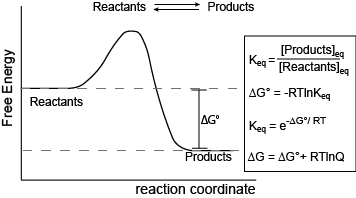
Figure 1. Reaction coordinate diagram for a generic exergonic reversible reaction. Equations relating Gibbs energy and the equilibrium constant: R = 8.314 J mol-1 K-1 or 0.008314 kJ mol-1 K-1; T is temperature in Kelvin. Attribution: Marc T. Facciotti (original work)
The figure above shows a commonly cited relationship between ∆G° and Keq:
∆Go=−RTlnKeq. (Chemical Equilibrium—Part 2.1)
Here, G° indicates the Gibbs energy under standard conditions (e.g., 1 atmosphere of pressure, 298 K). This equation describes the change in Gibbs energy for reactants converting to products in a reaction that is at equilibrium. The value of ∆G° can therefore be thought of as being intrinsic to the reactants and products themselves. ∆G° is like a potential energy difference between reactants and products. With this concept as a basis, one can also consider a reaction where the "starting" state is somewhere out of equilibrium. In this case, there may be an additional “potential” associated with the out-of-equilibrium starting state. This “added” component contributes to the ∆G of a reaction and can be effectively added to the expression for Gibbs energy as follows:
∆G=∆G°+RTlnQ, (Chemical Equilibrium—Part 2.2)
where Q is called the reaction quotient. From the standpoint of BIS2A, we will use a simple (a bit incomplete but functional) definition for
Q=[Products]st[Reactants]st (Chemical Equilibrium—Part 2.3)
at a defined non-equilibrium condition, st. One can extend this idea and calculate the Gibbs energy difference between two non-equilibrium states, provided they are properly defined and thus compute Gibbs energy changes between specifically defined out-of-equilibrium states. This last point is often relevant in reactions found in biological systems as these reactions are often found in multi-step pathways that effectively keep individual reactions in an out-of-equilibrium state.
This takes us to a point of confusion for some. In many biology books, the discussion of equilibrium includes not only the discussion of forward and reverse reaction rates, but also a statement that ∆G = 0 at equilibrium. This can be confusing because these very discussions often follow discussions of non-zero ∆G° values in the context of equilibrium (∆G° = -RTlnKeq). The nuance to point out is that ∆G° is referring to the Gibbs energy potential inherent in the chemical transformation between reactants and products alone. This is different from considering the progress of the reaction from an out-of-equilibrium state that is described by
∆G=∆Go+RTlnQ. (Chemical Equilibrium—Part 2.4)
This expression can be expanded as follows:
∆G=−RTlnKeq+RTlnQ (Chemical Equilibrium—Part 2.5)
to bring the nuance into clearer focus. In this case note that as Q approaches Keq that the reaction ∆G becomes closer to zero, ultimately reaching zero when Q = Keq. This means that the Gibbs energy of the reaction (∆G) reaches zero at equilibrium not that the potential difference between substrates and products (∆G°) reaches zero.


