6.8: Activation Energy
- Page ID
- 8405
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let's start to think a little about the rate of a reaction. Even exergonic (spontaneous) reactions typically require a small increase in free energy before they can begin converting reactants to products. This initial positive change in free energy is called the activation energy (or free energy of activation) and is sometimes abbreviated EA.
Note: possible discussion
The oxidation of gasoline is highly exergonic. Despite this, why do cars not spontaneously explode in parking lots?
Why do nearly all chemical reactions—even those with a very large negative ∆G—first require some free energy increase to proceed? The reason lies in the steps that take place during a chemical reaction. Chemical reactions, almost by definition, require that some chemical bonds be broken and/or formed. For example, when a glucose molecule is broken down, the glycosidic bonds are broken, bonds within water are broken and new bonds are made between the "disassembled" water and the atoms that were involved in the glycosidic bond. While the overall reaction (the combination of energy cost of breaking bonds, energy gained by making bonds, and the change of entropy between reactants and products) may be negative, the breaking of the bonds requires some energy input which increases the free energy of the system. The state of the reaction at the maximum free energy of a reaction is often termed the transition state. This state is considered to be relatively unstable in which the reaction may either relax back to the reactant state or transition to the products. The height of the activation energy "barrier" has a direct relationship to the rate of a reaction. The higher/larger the barrier, the slower the reaction.
Note: possible discussion
Can you propose a physical analog (or model) that can help explain why the activation energy barrier is related to the rate of the reaction, whereas the free energy difference between substrate and product is not.
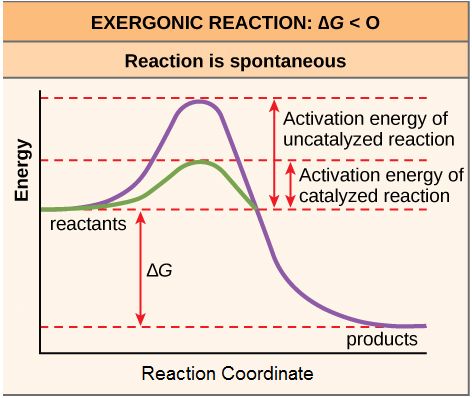
Figure 1. Activation energy is the energy required for a reaction to proceed, and it is lower if the reaction is catalyzed. The horizontal axis of this diagram describes the sequence of events in time.
Where does the free energy required required to overcome the activation energy barrier come from? The sources vary. One source is the energy transferred as heat from the surroundings. This transfer changes the kinetic energy of molecules in the system, increasing the frequency and force with which they collide and thus the frequency that they will react. In other cases, energy may be transferred from other reactions.
As noted, the activation energy of a particular reaction determines the rate at which it will proceed. The higher the activation energy, the slower the chemical reaction will be. The example of iron rusting illustrates an inherently slow reaction. The conversion of diamond into graphite is another spontaneous reaction that takes a LONG time. These reactions occur slowly over time because of high activation energy barriers. The burning (oxidation) of many fossil fuels, which is an exergonic process, will take place at a negligible rate unless their activation energy is overcome by sufficient heat from a spark. Once these fuels begin to burn, however, the chemical reactions release enough heat to help overcome the activation energy barrier for the combustion of the rest of the fuel. Like these reactions outside of cells, the activation energy for most cellular reactions is too high for heat energy to overcome at efficient rates. By the way, this is a very good thing as far as living cells are concerned. Important macromolecules, such as proteins, DNA, and RNA, store considerable energy, and their breakdown is exergonic. If cellular temperatures alone provided enough heat energy for these exergonic reactions to overcome their activation barriers, the essential components of a cell would disintegrate. Therefore, in order for important cellular reactions to occur at appreciable rates (number of reactions per unit time), their activation energies must be lowered (see figure 4). Something that helps lower the activation energy barrier is referred to as catalysis.
Note: possible discussion
If no activation energy were required to break down sucrose (table sugar), would you be able to store it in a sugar bowl?
Exercise 1: activation energy
Lowering the activation energy:
- Makes the reaction happen faster.
- Lowers the energy level of the transition state.
- Is accomplished by adding a catalyst to the reaction.
- Always causes more product to be produced.
- Only reduces the transition state energy level in one direction (from reactants to products).
- a, b, and c
- b and c
- All of the above are true.
Exercise 2
Which of the following comparisons or contrasts between endergonic and exergonic reactions are false?
- Endergonic reactions have a +∆G and exergonic reactions have a -∆G.
- Endergonic reactions consume energy and exergonic reactions release energy.
- Both endergonic and exergonic reactions require a small amount of energy to overcome an activation barrier.
- Endergonic reactions take place slowly and exergonic reactions take place quickly.
Exercise 3
Which of the following is the best way to judge the relative activation energies between two given chemical reactions?
- Compare the ∆G values between the two reactions.
- Compare their reaction rates.
- Compare their ideal environmental conditions.
- Compare the spontaneity between the two reactions.
Appendix: energy units
In the International System of Units (SI), the unit of work or energy is the Joule (J). For very small amounts of energy, the erg (erg) is sometimes used. An erg is one ten-millionth of a Joule:
1 Joule = 10,000,000 ergs (1)
Power is the rate at which energy is used. The unit of power is the Watt (W), named after James Watt, who perfected the steam engine:
1 Watt = 1 Joule/second (2)
Power is sometimes measured in horsepower (hp):
1 horsepower = 746 Watts (3)
Electrical energy is generally expressed in kilowatt-hours (kWh):
1 kilowatt-hour = 3,600,000 Joules (4)
It is important to realize that a kilowatt-hour is a unit of energy not power. For example, an iron rated at 2000 Watts would consume 2x3.6x106 J of energy in one hour.
Heat energy is often measured in calories. One calorie (cal) is defined as the heat required to raise the temperature of one gram of water from 14.5 to 15.5 ºC:
1 calorie = 4.189 Joules (5)
An old but still used unit of heat is the British Thermal Unit (BTU). It is defined as the heat energy required to raise the energy temperature of one pound of water from 63 to 64°F.
1 BTU = 1055 Joules (6)
| Physical quantity | Name | Symbol | SI unit |
|---|---|---|---|
| Force | Newton | N | kg*m/s2 |
| Energy | Joule | J | kg*m/s2 |
| Power | Watt | W | kg*m/s3 |