In contrast to micelles and bilayers, which are composed of aggregates of single and double chain amphiphiles, proteins are covalent polymers of 20 different amino acids, which fold, to a first approximation, in a thermodynamically spontaneous process into a single unique conformation, theoretically at a global energy minimum. This chapter section will investigate the possible conformations available to proteins, just as we studied the conformations of free fatty acids and acyl chains in lipid aggregates. The next chapter section will discuss the actual processes of folding and of unfolding (denaturation), both in vitro and in vivo. Then we will discuss the thermodynamics and intermolecular forces which stabilize the folded (or native) shape and the unfolded (or denatured state) of proteins, in a fashion similar to how we discussed micelle and bilayer stability.
Just as saturated fatty acid chains have preferred conformations (all ttt), peptide chains also have preferred conformations. The complexity is much greater, however. With fatty acid chains, we dealt only with torsion or dihedral angles around the methylene carbons. For proteins, we must consider the covalent links which attach the amino acids together, as well as the rotations possible in 20 different amino acids. The peptide bonds connect the carbonyl C of the i th amino acid to the alpha amine N of the i th+1 amino acid. The resulting bond is an amide link. X-ray analysis shows that the the C-N bond has double bond character. This can be accounted for by delocalizing the nonbonding electron pair of the N to the carbonyl C forming a double bond, with the pi bonded electrons of the carbonyl C-O bond moving to the O. These resonance structures lead to a planar arrangement of the peptide carbonyl C and amide N and the two other atoms connected to each, since the hybridization of the C and N has sp2 character, with 120° bond angles. This greatly simplifies the number of conformations which a protein can adopt since these 6 atoms can be considered to reside and move in a plane. The alpha C serves as the corner attachment point of two different planes, each which can rotate independently of the other plane. The two planes can twist around the alpha carbon. The rotation angles for the two planes are called phi (f) and psi(y) are analogous to the torsion angles in the acyl chains of fatty acid. They can vary from -180° to +180°. The R group substituent attached to the alpha C can also rotate around the alpha C and the beta C of the side chain. This angle is defined as chi. Other rotations also occur within the side chain. We will concentrate on phi (f) and psi(y) angles in this section.
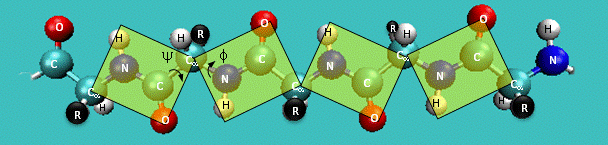
Figure: Extended Polypeptide Showing Planes and phi/psi Angles
Another important feature of the peptide bond is that the alpha Cs at opposite ends of the rectangle are usually trans to each other (on opposite sides of the C-N bond in the peptide bond. This trans arrangement of the alpha Cs is sterically favored by a factor of 1000/1 for all peptide bonds except X-Pro. Pro, which is a cyclic amino acid, is sterically restricted.
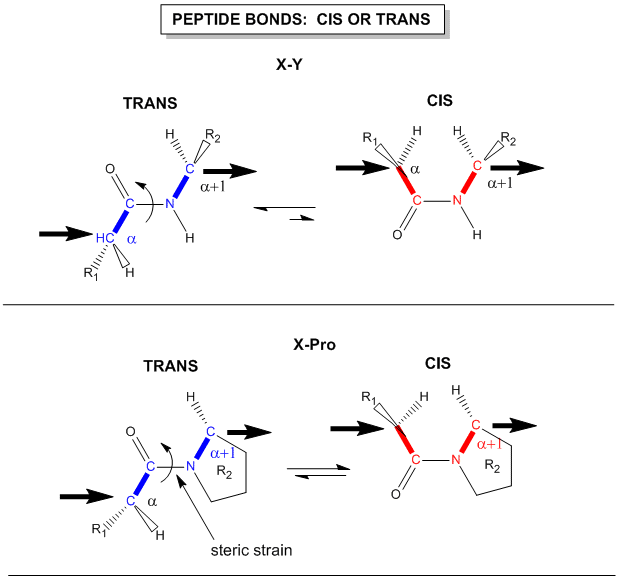
Figure: trans arrangement of the alpha Cs
The figure above, which also shows the X-Pro bond, clearly shows that both the trans and cis forms of the X-Pro bonds are hindered to a similar extent. In X-Pro bonds in proteins, the trans/cis ratio found in proteins is 4/1. The diagram above shows rans peptide bonds, and how they could be converted to cis through rotation around the C-N bond.
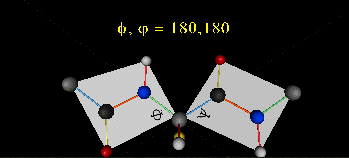
A protein can now be thought of as a series of linked sequences of rigid, planar peptide units which can rotate around phi/psi angles. When the chain is fully extended (as shown in the links above), phi/psi are 180°.
When phi (f) and psi(y) equal 0o, the two peptide bonds flanking the alpha Cs are in the same plane. This conformation is prohibited since the O of the C=O on one plane and the H of the H-N on the other are overlapping - i.e. they approach closer than their van der Waals radii.
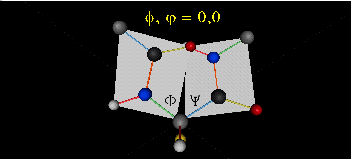
This simple example shows that all conformational space is not accessible for protein folding.
- Animation showing phi (f) angle rotation at psi (y)= 0.
- Animations showing psi (y) angle rotation at phi (f) = 0.
- Quick time movie (Alpha carbons are red. Move slider to approx. half way point to see "extended chain, analogous to the zig-zag conformation of the acyl chains in saturated fatty acids)
Ramachandran plot
Ramachandran was the first to calculate which phi/psi angles are allowed. He modeled the angles permitted to a tripeptide, assuming the atoms were hard spheres. The angles allowed depended in part on the limiting distance chosen for interatomic contacts. (i.e. the usual H -- H distance is 2.0 angstroms, and 3.0 for C--C bonds.) The plot below show the allowed regions in red. Only 3 small regions of conformational space are available. If you allow a closer approach by 0.1 angstrom, more conformation space is available, but only one new area is available (shown in yellow in the plot below).
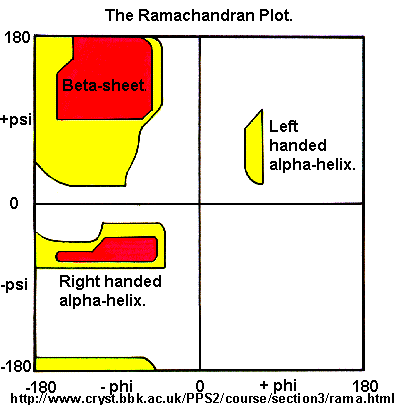
Figure: Ramachandran plot
A Ramachandran plot of Ala-Ala-Ala is nearly identical to the plot for Phe-Phe-Phe (which is unbranched at the beta carbon (the first methylene C in the side chain). The plot for Thr-Thr-Thr, which has a branch at the beta C (with OH and CH3 attached) shows somewhat less room than the other plots. Pro-Pro-Pro is most restricted for obvious reasons. For a longer chain than a tripeptide, there are more restrictions than for (Ala)3, since the chain can't assume a conformation when it passes through itself. The plots for actual proteins have many points which do fall in forbidden regions. However, these points would be allowed if the peptide bonds is twisted a few degrees. Gly bonds also fall outside the allowed regions. This is understandable, since the side chain of Gly is H, and it is used in protein where sharp turns of the chain is necessary. Right hand alpha helices fall at -57,-47 while left hand alpha helices fall at +57,+47. (Notice these are not mirror images of each other. The mirror image of a right-handed alpha helix would be a left handed helix made of D-amino acids.) Parallel beta sheets are at -119, -113, while antiparallel sheets falls at -139, +135. Other types of helices also are found. The 310 helix , a sharper helix with 3 amino acids/turn, falls at -49,-26. All of these examples of secondary structure fall in allowed regions. Modern Ramachandran plots do not model the atoms as hard spheres but instead consider the potential energy of the atoms using the Lennard-Jones potential (6-12 potential) for van der Waals interactions. We discussed this potential function in the molecular modeling lab.
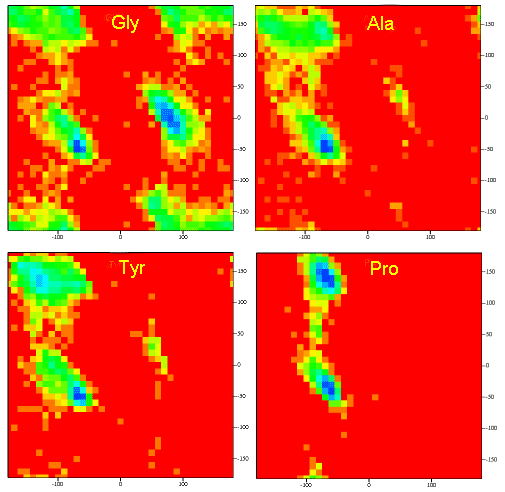
Figure: Ramachandran plots showing phi/psi angles for Gly, Ala, Tyr, and Pro in actual proteins
Contributors and Attributions








