In oxidation/reduction reactions, there is a transfer of charge - an electron - from one species to another. Oxidation is the loss of electrons and reduction is a gain in electrons. Use these acronyms to help you remember: Leo Ger - Loss of electrons oxidation; Gain of electrons reduction or Oil Rig - Oxidation involves loss, Reduction involves gain - of electrons.) These reactions always occur in pair. That is, an oxidation is always coupled to a reduction. When something gets oxidized, another agent gains those electrons, acting as the oxidizing agent, and gets reduced in the process. When a substance gets reduced, it gains electrons from something that gave them up, the reducing agent, which in the process gets oxidized. It's just like an acid base reaction. An acid reacts with a base to form a new acid and base.
Reactions in which a pure metal reacts with a substance to form a salts are clearly oxidation reactions. Consider for example the reaction of sodium metal and chlorine gas.
\[\mathrm{2Na(s) + Cl_2 \rightarrow 2NaCl(s)}\]
Na is a pure metal. (Although it really exists as sodium ions surrounded by a sea of electrons), consider it for our purposes to exist as elemental Na, which has a formal charge of 0. Likewise, Cl2 is a pure element. To determine the charge on each Cl atoms, we divide the two bonded electrons equally between the two Cl atoms, hence assigning 7 electrons to each Cl. Hence the formal charge on each Cl is 0.
In a similar fashion we can determine the oxidation number of an atom bonded to another atom. We can assign electrons to a bonded atoms, compare that number to the number in the outer shell of the unbonded atoms, and see if there is an excess or lack. In these cases, the same number of electrons get assigned to each atoms as when we are calculating formal charge. Hence the oxidation numbers are equal to the formal charge in these examples. Clearly, Na went from an oxidation number and formal charge of 0 to 1+ and Cl from 0 to 1-. Therefore, Na was oxidized by the oxidizing agent Cl2, and Cl2 was reduced by the reducing agent Na.
Let's consider other similar redox reactions:
- \(\mathrm{2Mg(s) + O_2(g) \rightarrow 2MgO(s)}\)
- \(\mathrm{Fe(s) + O_2(g) \rightarrow Fe\: oxides\: (s)}\)
- \(\mathrm{C(s) + O_2(g) \rightarrow CO_2(g)}\)
In the first two reactions, a pure metal (with formal charges and oxidation numbers of 0) lose electrons to form metal oxides, with positive metal ions. The oxygen goes form a formal charge and oxidation number of 0 to 2- and hence is reduced.
What about the last case? Each atom in both reactants and products has a formal charge of 0. This reaction, a combustion reactions with molecular oxygen, is also a redox reaction. Where are the electrons that are lost or gained?
This can be determined by assigning the electrons in the different molecules in a way slightly different than with formal charge. For shared (bonded) electrons, assign both electrons in the bond to the atom in the shared pair that has a higher electronegativity. Next calculate the apparent charge on the atom by comparing the number of assigned electrons to the usual number of outer shell electrons in an atom (i.e. the group number). This apparent charge is called the oxidation number. When using this method for the reaction of C to CO2, the C in carbon dioxide has an oxidation number of 4+ while the two oxygens have an oxidation number of 2- . Clearly, the C has "lost electrons" and has become oxidized by interacting with the oxidizing agent O2. as it went from C to CO2. If the atoms connected by a bond are identical, we split the electrons and assign one to each atom. In water, the O has an oxidation number of 2- while each H atom has an oxidation number of 1+. Notice that the sum of the oxidation numbers of the atoms in a species is equal to the net charge on that species.
What we have done is devise another way to count the electrons around an atom and the resulting charges on the atoms. See the animation below to review electron counting, and the 3 "types of charges" - partial charges, formal charges, and now oxidation numbers.
Consider an O-X bond, where X is any element other than F or O. Since O is the second most electronegative atom, the two electrons in the O-X bond will be assigned to O. In fact all the electrons around O (8) will be assigned to O, giving it always an oxidation number of 2-. This will be true for most molecules containing O we we encounter except for O2 and H2O2 (hydrogen peroxide), where the oxidations number for O are 0 and 1-, respectively. Now consider a C-H bond. Since C is nearer to F, O, and N than is H, we could expect C (en 2.5) to be more electronegative than H (en 2.1). Therefore, both electrons in the C-H bond are assigned to C, and H has an oxidation number of 1+. This will always be true for the molecules we study, except H-H. A quick summary of oxidation numbers shows that for the molecules we will study:
- O always has an oxidation # of 2- (except when it is bonded to itself or F)
- H always has an oxidation # of 1+ (except when it is bonded to itself)
- The sum of the oxidation numbers on a compound must equal the charge on the compound (just like the case of formal charges)
Notice in each of the reactions above, oxygen is an oxidizing agent. Also notice that in each of these reactions, a pure element is chemically changed into a compound with other elements. All pure, uncharged elements have formal charges and oxidation numbers of 0. When they appear as compounds in the products, they must have a different oxidation number. The disappearance or appearance of a pure element in a chemical reaction makes that reaction a redox reaction.
Now lets consider a more complicated case - the reaction of methane and oxygen to produce carbon dioxide and water:
\[\mathrm{CH_4 + O_2 \rightarrow H_2O + CO_2}\]
Since H has an oxidation # of 1+, the oxidation # of C in CH4 is 4-, while in CO2 it is 4+. Clearly C has been oxidized by the oxidizing agent O2. O2 has been reduced to form both products.
Now consider a series of step-wise reactions of CH4 ultimately leading to CO2
.
You should be able to determine that the oxidation numbers for the central C in each molecule are 4-, 2-, 0, 2+, and 4+ as you proceed from left to right, and hence represent step-wise oxidations of the carbon. Stepwise oxidations of carbon by oxidizing agents different than O2 are the hallmark of biological oxidation reactions. Each step-wise step releases smaller amounts of energy, which can be handled by the body more readily that if it occurred in "one step", as indicated in the combustion of methane by O2 above.
You may have learned in a previous course that in oxidation reactions, there is an increase in the number of X-O bonds, where X is some atom. Alternatively, it also involves the decrease of X-H bonds. Reduction would be the opposite case - decreasing the number of X-O bonds and/or increasing the number of X-H bonds. This rule applies well to the above step-wise example.
Now let's consider sulfur. in sulfhydrls and disulfides.
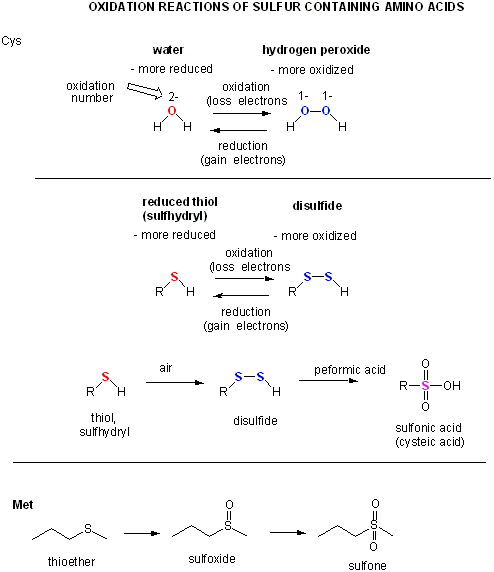
The oxidation number of S in RSH (2-) and in RSSH (1-) is the same as for O in ROH and ROOR. This must be true only if S is more electronegative than C. It is but not by much in the Pauling Scale (2.55 for C, 2.58 for S). In some general chemistry textbooks, the values are both given as 2.5. Other scales give different values as shown below.
| Scale | C | S |
| Pauling | 2.55 | 2.58 |
| Sanderson | 2.75 | 2.96 |
| Allred Rochow | 2.5 | 2.44 |
| Mulliken-Jaffe | 2.48 | 2.69 |
| Allen | 2.544 | 2.589 |
| Avg value for all | 2.56 | 2.65 |
Hence, S is more electronegative than C (or H) and its oxidation numbers are analogous to oxygen.
Contributors and Attributions




