11.2: Clade Age and Diversity
- Page ID
- 21643
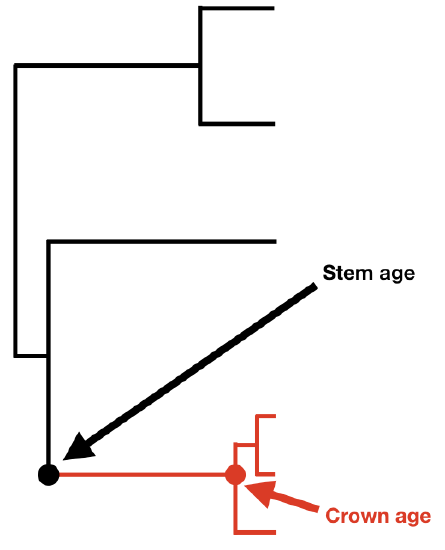
If we know the age of a clade and its current diversity, then we can calculate the net diversification rate for that clade. Before presenting equations, I want to make a distinction between two different ways that one can measure the age of a clade: the stem age and the crown age. A clade's crown age is the age of the common ancestor of all species in the clade. By contrast, a clade's stem age measures the time that that clade descended from a common ancestor with its sister clade. The stem age of a clade is always at least as old, and usually older, than the crown age.
Magallón and Sanderson (2001) give an equation for the estimate of net diversification rate given clade age and diversity:
\[ \hat{r} = \frac{ln(n)}{t_{stem}} \label{11.1}\]
where n is the number of species in the clade at the present day and tstem is the stem group age. In this equation we also see the net diversification rate parameter, r = λ − μ (see Chapter 10). This is a good reminder that this parameter best predicts how species accumulate through time and reflects the balance between speciation and extinction rates.
Alternatively, one can use tcrown, the crown group age:
\[ \hat{r} = \frac{ln(n)-ln(2)}{t_{crown}} \label{11.2}\]
The two equations differ because at the crown group age one is considering the clade's diversification starting with two lineages rather than one (Figure 11.2).
Even though these two equations reflect the balance of births and deaths through time, they give ML estimates for r only under a pure birth model where there is no extinction. If there has been extinction in the history of the clade, then our estimates using equations 11.1 and 11.2 will be biased. The bias comes from the fact that we see only clades that survive to the present day, and miss any clades of the same age that died out before they could be observed. By observing only the "winners" of the diversification lottery, we overestimate the net diversification rate. If we know the relative amount of extinction, then we can correct for this bias.
Under a scenario with extinction, one can define ϵ = μ/λ and use the following method-of-moments estimators from Rohatgi (1976, following the notation of Magallon and Sanderson (2001)):
\[ \hat{r} = \frac{log[n(1-\epsilon)+\epsilon]}{t_{stem}} \label{11.3}\]
for stem age, and
\[ \hat{r} = \frac{ln[\frac{n(1-\epsilon^2 )}{2}+2 \epsilon+\frac{(1-\epsilon) \sqrt{n(n \epsilon^2-8\epsilon+2 n \epsilon+n)}}{2}]-ln(2)}{t_{crown}} \label{11.4}\]
for crown age. (Note that eq. 11.3 and 11.4 reduce to 11.1 and 11.2, respectively, when ϵ = 0). Of course, we usually have little idea what ϵ should be. Common practice in the literature is to try a few different values for ϵ and see how the results change (e.g. Magallon and Sanderson 2001).
Magallón and Sanderson (2001), following Strathmann and Slatkin (1983), also describe how to use eq. 10.13 and 10.15 to calculate confidence intervals for the number of species at a given time.
As a worked example, let's consider the data in table 11.1, which give the crown ages and diversities of a number of plant lineages in the Páramo (from Madriñán et al. 2013). For each lineage, I have calculated the pure-birth estimate of speciation rate (from equation 11.2, since these are crown ages), and net diversification rates under three scenarios for extinction (ϵ = 0.1, ϵ = 0.5, and ϵ = 0.9).
| Lineage | n | Age | $\hat{r}_{pb}$ | $\hat{r}_{\epsilon = 0.1}$ | $\hat{r}_{\epsilon = 0.5}$ | $\hat{r}_{\epsilon = 0.9}$ |
|---|---|---|---|---|---|---|
| 1 | 17 | 0.42 | 5.10 | 5.08 | 4.53 | 2.15 |
| 2 | 14 | 10.96 | 0.18 | 0.18 | 0.16 | 0.07 |
| 3 | 32 | 3.80 | 0.73 | 0.73 | 0.66 | 0.36 |
| 4 | 65 | 2.50 | 1.39 | 1.39 | 1.28 | 0.78 |
| 5 | 55 | 3.05 | 1.09 | 1.08 | 1.00 | 0.59 |
| 6 | 120 | 4.04 | 1.01 | 1.01 | 0.94 | 0.62 |
| 7 | 36 | 4.28 | 0.68 | 0.67 | 0.61 | 0.34 |
| 8 | 32 | 7.60 | 0.36 | 0.36 | 0.33 | 0.18 |
| 9 | 66 | 1.47 | 2.38 | 2.37 | 2.19 | 1.34 |
| 10 | 27 | 8.96 | 0.29 | 0.29 | 0.26 | 0.14 |
| 11 | 5 | 3.01 | 0.30 | 0.30 | 0.26 | 0.09 |
| 12 | 46 | 0.80 | 3.92 | 3.91 | 3.58 | 2.07 |
| 13 | 53 | 14.58 | 0.22 | 0.22 | 0.21 | 0.12 |
The table above shows estimates of net diversification rates for Páramo lineages (data from Madriñán et al. 2013) using equations 11.2 and 11.4. Lineages are as follows: 1: Aragoa, 2: Arcytophyllum, 3: Berberis, 4: Calceolaria, 5: Draba, 6: Espeletiinae, 7: Festuca, 8: Jamesonia + Eriosorus, 9: Lupinus, 10: Lysipomia, 11: Oreobolus, 12: Puya, 13: Valeriana.
Inspecting the last four columns of this table, we can make a few general observations. First, these plant lineages really do have remarkably high diversification rates (Madriñán et al. 2013). Second, the net diversification rate we estimate depends on what we assume about relative extinction rates (ϵ). You can see in the table that the effect of extinction is relatively mild until extinction rates are assumed to be quite high (ϵ = 0.9). Finally, assuming different levels of extinction affects the diversification rates but not their relative ordering. In all cases, net diversification rates for Aragoa, which formed 17 species in less than half a million years, is higher than the rest of the clades. This relationship holds only when we assume relative extinction rates are constant across clades, though. For example, the net diversification rate we calculate for Calceolaria with ϵ = 0 is higher than the calculated rate for Aragoa with ϵ = 0.9. In other words, we can't completely ignore the role of extinction in altering our view of present-day diversity patterns.
We can also estimate birth and death rates for clade ages and diversities using ML or Bayesian approaches. We already know the full probability distribution for birth-death models starting from any standing diversity N(0)=n0 (see equations 10.13 and 10.15). We can use these equations to calculate the likelihood of any particular combination of N and t (either tstem or tcrown) given particular values of λ and μ. We can then find parameter values that maximize that likelihood. Of course, with data from only a single clade, we cannot estimate parameters reliably; in fact, we are trying to estimate two parameters from a single data point, which is a futile endeavor. (It is common, in this case, to assume some level of extinction and calculate net diversification rates based on that, as we did in Table 11.1 above).
One can also assume that a set of clades have the same speciation and extinction rates and fit them simultaneously, estimating ML parameter values. This is the approach taken by Magallón and Sanderson (2001) in calculating diversification rates across angiosperms. When we apply this approach to the Paramo data, shown above, we obtain ML estimates of $\hat{r} = 0.27$ and $\hat{\epsilon} = 0$. If we were forced to estimate an overall average rate of speciation for all of these clades, this might be a reasonable estimate. However, the table above also suggests that some of these clades are diversifiying faster than others. We will return to the issue of variation in diversification rates across clades in the next chapter.
We can also use a Bayesian approach to calculate posterior distributions for birth and death rates based on clade ages and diversities. This approach has not, to my knowledge, been implemented in any software package, although the method is straightforward (for a related approach, see Höhna et al. 2016). To do this, we will modify the basic algorithm for Bayesian MCMC (see Chapter 2) as follows.
Note
- Sample a set of starting parameter values, r and ϵ, from their prior distributions. For this example, we can set our prior distribution for both parameters as exponential with a mean and variance of λprior (note that your choice for this parameter should depend on the units you are using, especially for r). We then select starting r and ϵ from their priors.
- Given the current parameter values, select new proposed parameter values using the proposal density Q(p′|p). For both parameter values, we can use a uniform proposal density with width wp, so that Q(p′|p) U(p − wp/2, p + wp/2). We can either choose both parameter values simultaneously, or one at a time (the latter is typically more effective).
- Calculate three ratios:
- a. The prior odds ratio. This is the ratio of the probability of drawing the parameter values p and p′ from the prior. Since we have exponential priors for both parameters, we can calculate this ratio as: \[ R_{prior} = \frac{\lambda_{prior} e^{-\lambda_{prior} p'}}{\lambda_{prior} e^{-\lambda_{prior} p}}=e^{\lambda_{prior} (p-p')} \label{11.5}\[
- b. The proposal density ratio. This is the ratio of probability of proposals going from p to p′ and the reverse. We have already declared a symmetrical proposal density, so that Q(p′|p)=Q(p|p′) and Rproposal = 1.
- c. The likelihood ratio. This is the ratio of probabilities of the data given the two different parameter values. We can calculate these probabilities from equations 10.13 or 10.16 (depending on if the data are stem ages or crown ages).
- Find Raccept as the product of the prior odds, proposal density ratio, and the likelihood ratio. In this case, the proposal density ratio is 1, so (eq. 11.6):
Raccept = Rprior ⋅ Rlikelihood


