3.4: Brownian Motion on a Phylogenetic Tree
- Page ID
- 21589
We can use the basic properties of Brownian motion model to figure out what will happen when characters evolve under this model on the branches of a phylogenetic tree. First, consider evolution along a single branch with length t1 (Figure 3.4A). In this case, we can model simple Brownian motion over time t1 and denote the starting value as \(\bar{z}(0)\). If we evolve with some rate parameter σB2, then:
\[ E[\bar{z}(t)] \sim N(\bar{z}(0), \sigma_B^2 t_1) \label{3.17} \]
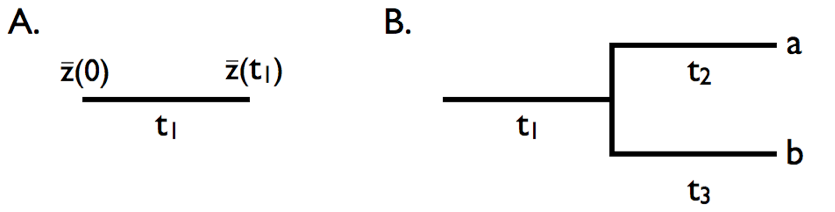
Now consider a small section of a phylogenetic tree including two species and an ancestral stem branch (Figure 3.4B). Assume a character evolves on that tree under Brownian motion, again with starting value \(\bar{z}(0)\) and rate parameter σB2. First consider species a. The mean trait in that species \(\bar{x}_a\) evolves under Brownian motion from the ancestor to species a over a total time of t1 + t2. Thus,
\[ \bar{x}_a \sim N[\bar{z}(0), \sigma_B^2 (t_1+t_2)] \label{3.18}\]
Similarly for species b, over a total time of t1 + t3
\[ \bar{x}_b \sim N[\bar{z}(0),\sigma_B^2 (t_1+t_3)] \label{3.19} \]
However, \( \bar{x}_a\) and \( \bar{x}_b\) are not independent of each other. Instead, the two species share one branch in common (branch 1). Each tip trait value can be thought of as an ancestral value plus the sum of two evolutionary changes: one (from branch 1) that is shared between the two species and one that is unique (branch 2 for species a and branch 3 for species b). In this case, mean trait values \( \bar{x}_a\) and \( \bar{x}_b\) will share similarity due to their shared evolutionary history. We can describe this similarity by calculating the covariance between the traits of species a and b. We note that:
\[ \begin{array}{lcr} \bar{x}_a = \Delta \bar{x}_1 + \Delta \bar{x}_2\\ \bar{x}_b = \Delta \bar{x}_1 + \Delta \bar{x}_3\\ \end{array} \label{3.20} \]
Where \(\Delta \bar{x}_1\), \(\Delta \bar{x}_2\), and \(\Delta \bar{x}_3\) represent evolution along the three branches in the tree, are all normally distributed with mean zero and variances σ2t1, σ2t2, and σ2t3, respectively. \(\bar{x}_a\) and \(\bar{x}_b\) are sums of normal random variables and are themselves normal. The covariance of these two terms is simply the variance of their shared term:
\[ cov(\bar{x}_a,\bar{x}_b)=var(\Delta \bar{x}_1)=\sigma_B^2 t_1 \label{3.21} \]
It is also worth noting that we can describe the trait values for the two species as a single draw from a multivariate normal distribution. Each trait has the same expected value, \(\bar{z}(0)\), and the two traits have a variance-covariance matrix:
\[ \begin{bmatrix} \sigma^2 (t_1 + t_2) & \sigma^2 t_1 \\ \sigma^2 t_1 & \sigma^2 (t_1 + t_3) \\ \end{bmatrix} = \sigma^2 \begin{bmatrix} t_1 + t_2 & t_1 \\ t_1 & t_1 + t_3 \\ \end{bmatrix} = \sigma^2 \mathbf{C} \label{3.22} \]
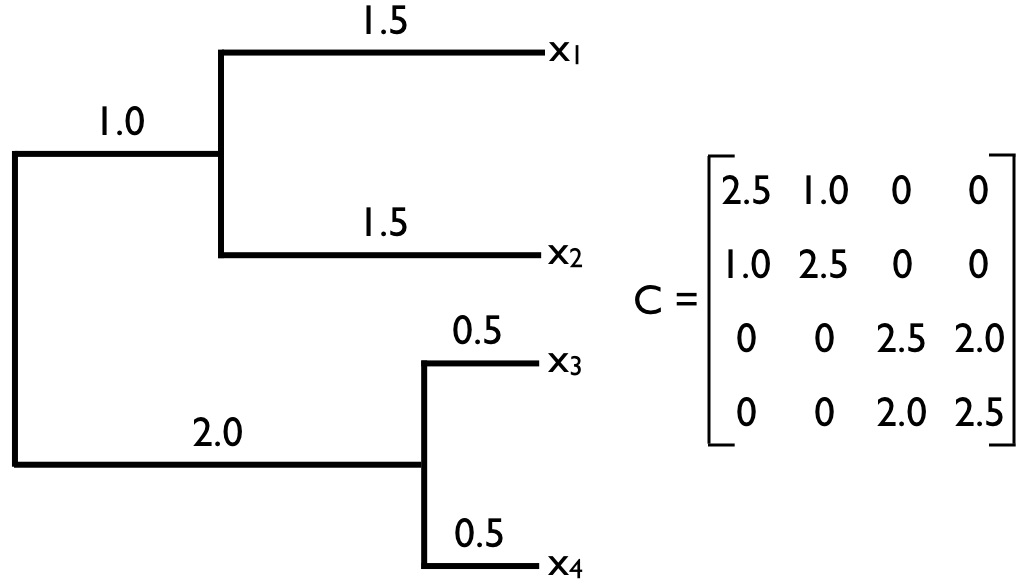
The matrix C in Equation \ref{3.22} is commonly encountered in comparative biology, and will come up again in this book. We will call this matrix the phylogenetic variance-covariance matrix. This matrix has a special structure. For phylogenetic trees with n species, this is an n × n matrix, with each row and column corresponding to one of the n taxa in the tree. Along the diagonal are the total distances of each taxon from the root of the tree, while the off-diagonal elements are the total branch lengths shared by particular pairs of taxa. For example, C(1, 2) and C(2, 1) – which are equal because the matrix C is always symmetric – is the shared phylogenetic path length between the species in the first row – here, species a - and the species in the second row – here, species b. Under Brownian motion, these shared path lengths are proportional to the phylogenetic covariances of trait values. A full example of a phylogenetic variance-covariance matrix for a small tree is shown in Figure 3.5. This multivariate normal distribution completely describes the expected statistical distribution of traits on the tips of a phylogenetic tree if the traits evolve according to a Brownian motion model.