8.6: Current Research Directions, What Have We Learned?, Bibliography
- Page ID
- 40965
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- HMM’s have been used extensively in various fields of computational biology. One of the first such applications was in a gene-finding algorithm known as GENSCAN written by Chris Burge and Samuel Karlin [1]. Because the geometric length distribution of HMM’s does not model exonic regions well, Burge et. al used an adaptation of HMM’s known as hidden semi-Markov models (HSMM’s). These types of models differ in that whenever a hidden state is reached, the length of duration of that state (di) is chosen from a distribution and the state then emits exactly di characters. The transition from this hidden state to the next is then analogous to the HMM procedure except that akk = 0 for all k, thereby preventing self-transitioning. Many of the same algorithms that were previously developed for HMM’s can be modified for HSMM’s. Although the details won’t be discussed here, the forward and backward algorithms can be modified to run in O(K2N3) time, where N is the number of observed characters. This time complexity assumes that there is no upper bound on the length of a state’s duration, but imposing such a bound reduces the complexity to O(K2ND2), where D is the maximum possible duration of a state.
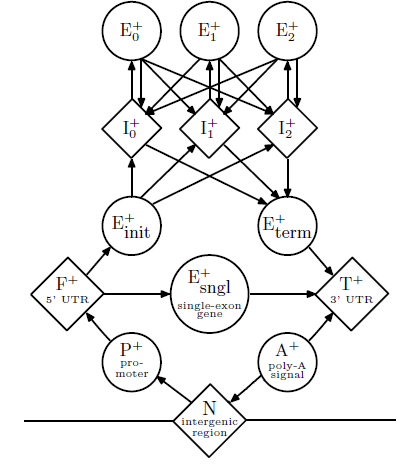
The basic state diagram underlying Burge’s model is depicted in Figure 8.7. The included diagram only lists the states on the forward strand of DNA, but in reality a mirror image of these states is also included for the reverse strand, resulting in a total of 27 hidden states. As the diagram illustrates, the model incorporates many of the major functional units of genes, including exons, introns, promoters, UTR’s and poly-A tails. In addition, three different intronic and exonic states are used to ensure that the total length of all exons in a gene is a multiple of three. Similar to the CpG island example, this expanded state-space enabled the encoding of memory within the model.
- A recent effort has been made to make an HMM-based approach to homology searches, called HMMER, a viable alternative to BLAST in terms of computational efficiency. Unlike most other homology search algorithms, HMMER, written by Sean Eddy, uses the Forward algorithm’s average over alignment un- certainty, rather than only reporting the maximum likelihood alignment (a la Viterbi ); this approach is often better for detecting more remote homologies, as as divergence times increase, there may become more viable ways of aligning sequences, each of them individually not sufficiently strong to be differentiated from noise but together giving evidence for homology. A particularly exciting recent development is that HMMER is now available as a web server; it can be found at http://www.ebi.ac.uk/Tools/hmmer/.
- An interesting subject that may be explored also concerns the agreement of Viterbi and Posterior decoding paths; not just for CpG island detection but even for chromatin state detection. One may look at multiple paths by sampling, asking questions such as:
– What is the maximum a posteriori vs viterbi path? Where do they differ?
– Can complete but maximally disjoint (from Viterbi) paths be found?
