A3. Amino Acid Charges
- Page ID
- 4690
Monomeric amino acids have an alpha amino group and a carboxyl group, both of which may be protonated or deprotonated, and a R group, some of which may be protonated or deprotonated. When protonated, the amino group has a +1 charge, and the carboxyl group a 0 charge. When deprotonated the amino group has no charge, while the carboxyl group has a -1 charge. The R groups which can be protonated/deprotonated include Lys, Arg and His, which have a + 1 charge when protonated, and Glu and Asp (carboxylic acids), Tyr and Ser (alcohols) and Cys (thiol), which have 0 charge when protonated. Of course, when the amino acids are linked by peptide bonds (amide link), the alpha N and the carboxyl C are in an amide link, and are not charged. However, the amino group of the N -terminal amino acid and the carboxyl group of the C-terminal amino acid of a protein may be charged. The Henderson Hasselbach equation gives us a way to determine the charge state of any ionizable group knowing the pKa of the group. Write each functional group capable of being deprotonated as an acid, HA, and the deprotonated form as A. The charge of HA and A will be determined by the functional group. The Ka for the reaction is:
\[\mathrm{K_a = \dfrac{[H_3O^+][A]}{[HA]}}\]
or
\[\mathrm{[H_3O^+ ] = K_a\dfrac{[HA ]}{[A]}}\]
\[\mathrm{ - log [H_3O^+] = -log K_a + log \dfrac {[A]}{[HA]}}\]
or
\[\mathrm{pH = pK_a + log \dfrac{[A]}{[HA]}}\]
This is the (in)famous Henderson-Hasselbach (HH) equation.
The properties of a protein will be determined partly by whether the side chain functional groups, the N terminal, and the C terminal are charged or not. The HH equation tells us that this will depend on the pH and the pKa of the functional group.
- If the pH is 2 units below the pKa, the HH equation becomes, -2 = log A/HA, or .01 = A/HA. This means that the functional group will be about 99% protonated (with either 0 or +1 charge, depending of the functional group).
- If the pH is 2 units above the pKa, the HH equation becomes 2 = log A/HA, or 100 = A/HA. Therefore the functional group will be 99% deprotonated.
- If the pH = pka, the HH equation becomes 0 = log A/HA, or 1 = A/HA. Therefore the functional group will be 50% deprotonated
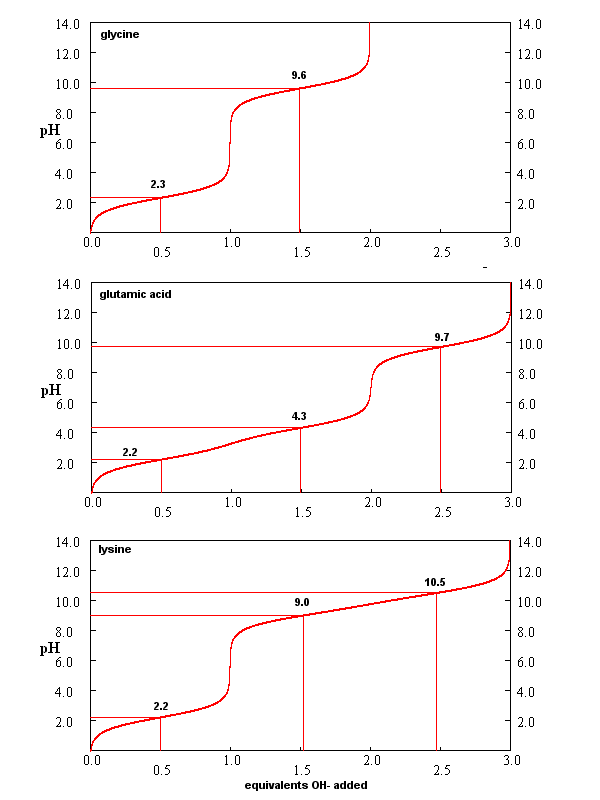
From these simple examples, we have derived the +2 rule. This rule is used to quickly determine protonation, and hence charge state, and is extremely important to know (and easy to derive). Titration curves for Gly (no ionizable) side chain, Glu (carboxlic acid side chain) and Lys (amine side chain) are shown below. You should be able to associate various sections of these curves with titration of specific ionizable groups in the amino acids.
Figure: Titration curves for Gly, Glu, and Lys
Buffer Review
The Henderson-Hasselbach equation is also useful in calculating the composition of buffer solutions. Remember that buffer solutions are composed of a weak acid and its conjugate base. Consider the equilibrium for a weak acid, like acetic acid, and its conjugate base, acetate:
\[\mathrm{CH_3CO_2H + H_2O \Leftrightarrow H_3O^+ + \sideset{}{_{2}^{-}}{CH_3CO}}\]
If the buffer solution contains equal concentrations of acetic acid and acetate, the pH of the solution is:
\[\mathrm{pH = pK_a + log \dfrac {[A]}{[HA]} = 4.7 + log\ 1 = 4.7}\]
A look at the titration curve for the carboxyl group of Gly (see above) shows that when the pH = pKa, the slope of the curve (i.e. the change in pH with addition of base or acid) is at a minimum. As a general rule of thumb, buffer solution can be made for a weak acid/base in the range of +/- 1 pH unit from the pKa of the weak acids. At the pH = pKa, the buffer solution best resists addition of either acid and base, and hence has its greatest buffering ability. The weak acid can react with added strong base to form the weak conjugate base, and the conjugate base can react with added strong acid to form the weak acid (as shown below) so pH changes on addition of strong acid and base are minimized.
- addition of strong base produces weak conjugate base: \(\mathrm{CH_3CO_2H + OH^- \rightarrow \sideset{}{_{2}^{-}}{CH_3CO} + H_2O}\)
- addition of strong acid produces weak acid: \(\mathrm{H_3O^+ + \sideset{}{_{2}^{-}}{CH_3CO} \rightarrow CH_3CO_2H + H_2O}\)
There are two simples ways to make a buffered solution. Consider an acetic acid/acetate buffer solution.
- make equal molar solution of acetic acid and sodium acetate, and mix them, monitoring pH with a pH meter, until the desired pH is reached (+/- 1 unit from the pKa).
- take a solution of acetic acid and add NaOH at substoichiometric amounts until the desired pH is reached (+/- 1 unit from the pKa). In this method you are forming the conjugate base, acetate, on addition of the weak base:
\[\mathrm{CH_3CO_2H + OH^- \rightarrow \sideset{}{_{2}^{-}}{CH_3CO} +\, H_2O}\]
 Buffers for pH control: Recipes based on pKas for acids, temperature, and ionic strength
Buffers for pH control: Recipes based on pKas for acids, temperature, and ionic strength
Isoelectric Point
What happens if you have many ionizable groups in a single molecule, as is the case with a polypeptide or protein. Consider a protein. At a pH of 2, all ionizable groups would be protonated, and the overall charge of the protein would be positive. (Remember, when carboxylic acid side chains are protonated, their net charge is 0.) As the pH is increased, the most acidic groups will start to deprotonate and the net charge will become less positive. At high pH, all the ionizable groups will become deprotonated in the strong base, and the overall charge of the protein will be negative. At some pH, then, the net charge will be 0. This pH is called the isoelectric point (pI). The pI can be determined by averaging the pKa values of the two groups which are closest to and straddle the pI. One of the online problems will address this in more detail
- LIst of pI and MW for proteins derived from 2D gels
Remember that pKa is really a measure of the equilibrium constant for the reaction. And of course, you remember that DGo = -RT ln Keq. Therefore, pKa is independent of concentration, and depends only on the intrinsic stability of reactants with respect to the products. This is true only AT A GIVEN SET OF CONDITIONS, SUCH AS T, P, AND SOLVENT CONDITIONS.
Consider, for example acetic acid, which in aqueous solution has a pKa of about 4.7. It is a weak acid, which dissociates only slightly to form H+ (in water the hydronium ion, H3O+, is formed) and acetate (Ac-). These ions are moderately stable in water, but reassociate readily to form the starting product. The pKa of acetic acid in 80% ethanol is 6.87. This can be accounted for by the decrease in stability of the charged products which are less shielded from each other by the less polar ethanol. Ethanol has a lower dielectric constant than does water. The pKa increases to 10.32 in 100% ethanol, and to a whopping 130 in air!
- A great interactive web site: Amino Acid Acid/Base Titration Curves
- pI calculator for any protein sequence
- Amino Acid Repository: Properties of Amino Acids


