A. Reactions and Energy Changes
- Page ID
- 4673
Why do reactions vary in extent from completely irreversible in the forward reaction to reversible reactions favoring the reactants? It might help to understand a simple physical reaction before we try more complicated chemical reactions.
Ball on a hill. Does a ball at the top of a hill roll downhill spontaneously, or does the opposite happen? No one has ever seen a ball roll spontaneously uphill unless a lot of energy was added to the ball. This physical reaction appears to be irreversible, and occurs because the ball has lower potential energy at the bottom of the hill than it does at the top. The gap in the potential energy is related to the "extent" and spontaneity of this reaction. As we have observed before, nature tends to go to a lower energy state. By analogy, we will consider the driving force for a chemical reaction to be the free energy difference between reactants and products. The standard free energy difference, ΔGo, describes the extent of the reaction when it has reached equilibrium, and the free energy difference, ΔG, desribes the spontaneity of the reaction to undergo a chnage from a specific set of starting concentrations to a specific set of ending conditions (often equilibrium).
For physical changes such as a ball rolling down a hill, or a compound undergoing a phase change, there is no ΔGo value because there is no equilibrium state equivalent to the equilibrium state of a chemical reaction. In other words, a ball rolling down hill does not stop part of the way down, nor will there be any ice left in a glass of water that is above 0oC.
ANIMATION: BALL ON A HILL - WHAT YOU ALWAYS SEE!
ANIMATION: BALL ON A HILL - WHAT YOU NEVER SEE!
Reversible/Irreversible Reactions, Extent of Reactions, Equilibrium: Consider a hypothetical reversible reaction in which you start with some reactants, A and B, each at a 1 M concentration (1 mol of each/L solution). but no products, P and Q. For ease assume that the total volume of solution is 1 L, so that we start with 1 mol each of A and B . At time t=0, the concentration of products is 0. The reaction can be written as:
\[\mathrm{A + B \leftrightarrow P + Q}\]
As time progresses, the amounts or concentrations of A and B decrease as the amounts or concentrations of products P and Q increase. At some time, no further changes occur in the amount or concentrations of remaining reactants or products. At this point the reaction is in equilibrium, a term used often in our common vocabulary to denote a system that is undergoing no net change.
Most of the reactions that we will study occur in solution, so we will deal with concentrations (in mol/L or mmol/mL = M). Lets consider how the concentration of reactants and products change as a function of time. Depending on the extent to which a reaction is reversible, 4 different scenarios can be imagined:
Scenario 1: Irreversible reaction in which the reverse reaction occurs to a negligible extent.
In this reaction, the reverse reaction occurs to such a small extent that we can neglect it. The only reaction that occurs is the conversion of reactants to product. Hence all the reactants are converted to product. At equilibrium [A] = 0. Since 1 mol of A reacted, it must form 1 mol of P and 1 mol Q - i.e. the concentration of products at equilibrium is 1 M. At an earlier time of the reaction, (let's pick a time when [A] = 0.8 M), only part of the reactants have reacted (in this case 0.2 M), producing an equal amount of products, P and Q. Graphs of [A] and [P] as a function of timer are shown below. [A] decreases in a nonlinear fashion to 0 M while [P] increases in a reciprocal fashion to 1 M concentration. This is illustrated in the graph below.
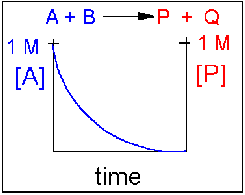
Examples of irreversible reactions are reactions of strong acids (nitric, sulfuric, hydrochloric) with bases (OH- and water), or combustion reactions like the burning of sugars (like trees) and hydrocarbons (like octane) to form CO2 and H2O.
Scenario 2: Reversible reaction in which the forward reaction is favored.
Again [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As [A ]and [B] decrease, [P] and [Q] increase, which increases the chance that they will collide and form product. Since P and Q can react to form reactants, the [A] at equilibrium is not zero as is shown below.
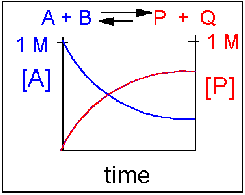
Scenario 3: Reversible Reaction in which forward and reverse reactions are equally favored.
Again [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As [A] and [B] decrease, [P] and [Q] increase, which increases the chance that they will collide and form product. Since P and Q can react to from reactants, the [A] at equilibrium is not zero as is show below. Because the reactants and products are equally favored, their concentrations will be equal at equilibrium .
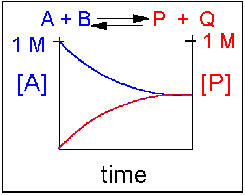
Scenario 4: Reversible Reaction in which the reverse reaction is favored.
Again [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As [A] and [B] decrease, [P] and [Q] increase, which increases the chance that they will collide and form product. Since P and Q can react to from reactants, the [A] at equilibrium is not zero as is show below. Because the reaction favors reactants. their concentration will be higher at equilibrium than the products.
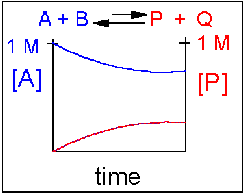
An example of this kind of reaction, one that favors reactants, is the reaction of acetic acid (a weak acid) with water.
\[\mathrm{CH_3CO_2H(aq) + H_2O(l) \Leftrightarrow + H_3O^+(aq) + \sideset{}{_{2}^{-}}{CH_3CO}(aq)}\]


