Reduction/Oxidation Reactions#

Reduction-Oxidation Reactions

In this class we are going to focus on REDOX reactions that are biologically associated. The majority of the reactions we discuss occur in the context of metabolic pathways (connected sets of metabolic reactions) where compounds may be consumed by the cell, broken down into smaller parts and then reassembled into larger macromolecules.

Lets start with some Generic Reactions

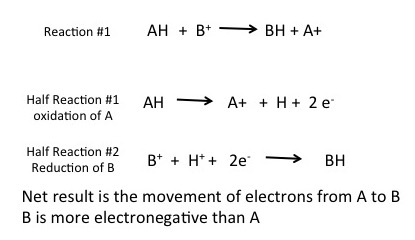
Transferring electrons between two compounds results in one of these compounds loosing an electron, and one of the compounds gaining an electron. For example, look at the figure below. If we use the energy story rubric to look at the overall reaction we can compare the before and after characteristics of the reactants and products. What happens to the matter (stuff) before and after the reaction? Compound A starts as neutral and becomes positively charged. Compound B starts as neutral and becomes negatively charged. Because electrons are negatively charged, we can follow the movement of electrons from compound A to B by looking at the change in charge. A looses an electron (becoming positively charged), and in so doing we say that A has become oxidized. Oxidation is associated with the loss of electron(s). B gains the electron (becoming negatively charged), and we say that B has become reduced. Reduction is associated with gain of electrons. We also know, since something happened that energy must have been either transferred and/or reorganized in this process and we'll consider this shortly.

In Bis2A we expect you to become familiar with this terminology. Try to learn it and learn to use it as soon as possible - we will use the terms frequently and will not have the time to define them each time.

A generic redox reaction. The full reaction is A +B goes to A⁺ + B^-. The two half reactions are shown in the blue box. A is oxidized by the reaction and B is reduced by the reaction.

When an electron(s) is lost, or a molecule is oxidized, the electron(s) must then passed to another molecule. The molecule gaining the electron is said to be reduced. The oxidation and reduction reactions are always paired in what is known as an oxidation-reduction reaction (also called a red/ox reaction).

For emphasis: In Bis2a we expect you to become familiar with this terminology. Try to learn it and learn to use it as soon as possible - we will use the terms frequently and will not have the time to define them each time.

Remember the Definitions:

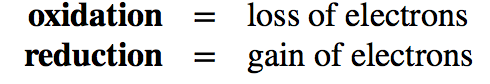
The Half Reaction

To formalize our common understanding of red/ox reactions, we introduce the concept of the half reaction. Two half reactions are required to make the full red/ox reaction. Each half reaction can be thought of as a description of what happens to one of the two molecules involved in the red/ox reaction. This is illustrated below. In this example compound AH is being oxidized by compound B⁺; electrons are moving from AH to B⁺ to generate A⁺ and BH. Each reaction can be thought of as two half reactions: Where AH is being oxidized and a second reaction where B⁺ is being reduced to BH. These two reactions are considered coupled, a term that indicates that these two reactions occur together, at the same time.

Generic red/ox reaction where compound AH is being oxidized by compound B⁺. Each half reaction represents a single species or compound to either lose or gain electrons (and a subsequent proton as shown in the figure above). In half reaction #1 AH loses a proton and 2 electrons: in the second half reaction, B⁺ gains 2 electrons and a proton. In this example HA is oxidized to A⁺ while B⁺ is reduced to BH.

Note: Possible discussion

If you consider a generic redox reaction and reflect back on the thermodynamic lectures what factor will determine whether a redox reaction will "go" in a particular direction spontaneously and what might determine its rate?

Reduction Potential

By convention we analyze and describe red/ox reactions with respect to reduction potentials, a term that quantitatively describes the "ability" of a compound to gain electrons. This value of the reduction potential is determined experimentally but for the purpose of this course we assume that the reader will accept that the reported values are reasonably correct. We can anthropomorphize the reduction potential by saying that it is related to the strength with which a compound can “attract” or “pull” or “capture” electrons. Not surprisingly this is is related to but not identical to electronegativity.

What is this intrinsic property to attract electrons?

Different compounds, based on their structure and atomic composition have intrinsic and distinct attractions for electrons. This quality is termed reduction potential or E0’and is a relative quantity (relative by comparison to some “standard” reaction). If a test compound has a stronger "attraction" to electrons than the standard (if the two competed the test compound would "take" electrons from the standard compound), we say that the test compound has a positive reduction potential whose magnitude is proportional to how much more it "wants" electrons than the standard compound. The relative strength of the compound in comparison to the standard is measured and reported in units of Volts (V)(sometimes written as electron volts or eV) or milliVolts (mV). The reference compound in most redox towers is H₂.

Note: Possible discussion

Rephrase for yourself: How do you describe or think about the difference between the concept of electronegativity and redox potential?

The Redox Tower

All kinds of compounds can participate in redox reactions. A tool has been developed to graphically tabulate redox half reactions based on their E₀^' values and to help us predict the direction of electron flow between potential electron donors and acceptors. Whether a particular compound can act as an electron donor (reductant) or electron acceptor (oxidant) depends critically on what other compound it is interacting with. The electron tower usually ranks a variety of common compounds (their half reactions) from most negative E₀^', compounds that readily get rid of electrons, to the most positive E₀^', compounds most likely to accept electrons. In addition, each half reaction is written by convention with the oxidized form on the left/followed by the reduced form on the right of the slash.
For example the half reaction for the reduction of NAD⁺ to NADH is written:
NAD⁺/NADH. In the tower below, the number of electrons that are transferred is also listed. For example the reduction of NAD⁺ to NADH involves two electrons, written in the table as 2e^-.

An electron tower is shown below.

Common Red/ox tower used in Bis2A. By convention the tower half reactions are written with the oxidized form of the compound on the left and the reduced form on the right. Compounds that make excellent electron donors are found at the top of the tower. Compounds such as Glucose and Hydrogen gas are excellent electron donors. Notice, that they are found on the right hand side of the red/ox pair half reactions. At the other end of the tower lies compounds that make excellent terminal electron acceptors, such as Oxygen and Nitrite, these compounds are found on the left side of the red/ox pair and have a positive E₀^' value.

Video on electron tower

For a short video on how to use the electron tower in red/ox problems click here. This video was made by Dr. Easlon for Bis2A students. (This is quite informative.)

What is the relationship between ΔE₀^' and ΔG?

The question now becomes: how do we know if any given redox reaction is energetically spontaneous or not (exergonic or endergonic) and regardless of direction, what the free energy difference is? The answer lies in the difference in the reduction potentials of the two compounds. The difference in the reduction potential for the reaction or E0' for the reaction, is the difference between the E₀^' for the oxidant (the compound getting the electrons and causing the oxidation of the other compound) and the reductant (the compound losing the electrons). In our generic example below, AH is the reductant and B⁺ is the oxidant. Electrons are moving from AH to B⁺. Using the E₀^' of -0.32 for the reductant and 0.82 for the oxidant the total change in E₀^' or ΔE0' is 1.14 eV.

Generic redox reaction with half reactions written with reduction potential (E₀^') of the two half reactions indicated.

The change in ΔE₀^' correlates to changes in Gibbs free energy, ΔG. In general a large positive ΔE₀^' is proportional to a large negative ΔG. The reactions are exergonic and spontaneous. For a reaction to be exergonic the reaction needs to have a negative change in free energy or -ΔG, this will correspond to a positive ΔE₀^'. In other words, when electrons flow "downhill" in a redox reaction from a compound with a higher (more positive) reduction potential to a second compound with a lower (less positive) reduction potential, they release free energy. The greater the voltage, ΔE₀^', between the two components, the greater the energy available when electron flow occurs. It is, in fact, possible to quantify the amount of free energy available. The relationship is given by the Nernst equation:

The Nernst equation relates free energy of a redox reaction to the difference in reduction potential between the reduced products of the reaction and oxidized reactant.
Attribution: Marc T. Facciotti (original work)

Where:

• n is the number of moles of electrons transferred
• F is the Faraday constant of 96.485 kJ/V. Sometimes it is given in units of kcal/V which is 23.062 kcal/V, which is the amount of energy (in kJ or kcal) released when one mole of electrons passes through a potential drop of 1 volt

Note

What you should notice is that ΔG and ΔE have an inverse relationship: When ΔG is positive, ΔE is negative and when ΔG is negative, ΔE is positive. For additional review see the redox discussion in the Bis2A Discussion Manual.