C. Change in Free Energy G
- Page ID
- 4675
The total ΔG can be expressed as the sum of the two contributions showing the effects of the intrinsic stability (Keq) and concentration:
ΔG = ΔGstab + ΔGconc
ΔG = ΔGo + RTlnQrx = ΔGo + RTln ([P][Q])/([A][B])
for the reaction A + B <=> P + Q, where ΔGoreflects the contribution from the relative intrinsic stability of reactants and products) and RTlnQrx reflects the contribution from the relative concentrations of reactants and products (which has nothing to do with stability). Qrx is the reaction quotient which for the reaction A + B <=> P + Q is given by:
Qrx = ([P][Q])/([A][B])
Meaning of ΔG
Remember that ΔG is the "driving" force for a reaction, analogous to the difference in potential energy for a ball on a hill. Go back to that analogy. if the ball starts at the top of the hill, does it roll down hill? Of course. It goes from high potential energy to low potential energy. The reaction can be written as: Balltop --> Ballbottom for which the change in potential energy, ΔPE = PEbottom -PEtop< 0. If the ball starts at the bottom, will it go to the top? Obviously not. For that reaction, Ballbottom --> Balltop, ΔPE > 0. If the top of the hill was at the same height at the bottom of the hill (obviously an absurd situation), the ball would not move. It would effectively be at equilibrium, a state of no change. For this reaction, Balltop --> Ballbottom, the ΔPE = 0. As the ball starts rolling down the hill, its potential energy gets closer to the potential it would have at the bottom. Hence the ΔPE changes from negative to more and more positive until it gets to the bottom at which case the ΔPE = 0 and movement ceases. If the ΔPE is not 0, the ball will move until the ΔPE = 0.
Likewise, for a chemical reaction that favors products, ΔG < 0. The system is not at equilibrium and the reaction will go in the direction of products. As the reaction proceeds, products build up, and there is less of a driving force for reactants to go to products (LeChatilier's Principle), so the ΔG becomes more a more positive until the ΔG = 0 and the reaction is at equilibrium. A reaction that has a ΔG > 0 is likewise not at equilibrium so it will go in the appropriate direction until equilibrium is reached. Hence for the reaction A + B <==> P + Q,
- if ΔG < 0, the reaction goes toward products P and Q
- if ΔG = 0, the reaction is at equilibrium and no further change occurs in the concentration of reactants and products.
- if ΔG > 0, the reaction goes toward reactants A and B.
We can not measure easily the actual free energy G of reactants or products, but we can measure ΔG readily. These points are illustrated in the graph below of ΔG vs time for the hypothetical reaction A + B <==> P + Q. (Also notice the two insert graphs - in blue and red - which show, in analogy to the ball on the hill graphs, the values of ΔG at the two points where the perturbation to the equilibrium were made.)
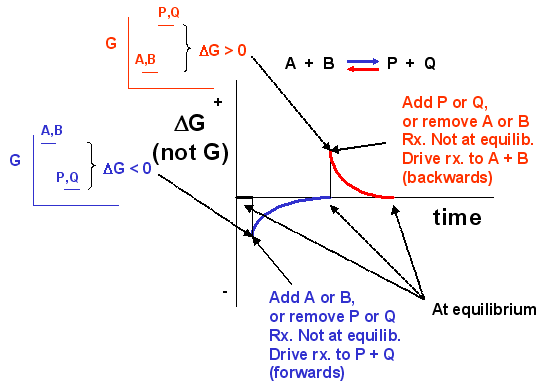
Notice the ΔG is constantly changing until the system reaches equilibrium. Initially the equilibrium is perturbed so that the system is not in equilibrium (shown in blue). The perturbation was such that the products are favored. After equilibrium was reached, the system was perturbed again, this time in a fashion to favor the reverse reaction. Notice in this case the ΔG for the reaction as written: A + B <==> P + Q is positive - i.e. it is not in equilibrium. Therefore the reaction (as written) goes backwards to products. It is important to realize that the reported ΔG is for the reaction as written.
Now let's apply ΔG = ΔGo + RTln Q = ΔGo + RTln ([P][Q])/([A][B]) to two reactions we discussed above:
- HCl(aq) + H2O(l) <==>H3O+(aq) + Cl-(aq)
- CH3CO2H(aq) + H2O(l) <==> H3O+(aq) + CH3CO2-(aq)
Assume that at time t=0, 0.1 mole of HCl and CH3CO2H were added to two different beakers. At this point the forward reaction are favored, but obviously to different extents. The RTln Q would be identical for both acids, since each reactant is present at 0.1 M, but no products yet exist. However, the ΔGois negative for HCl and positive for acetic acid since HCl is a strong acid. Hence at t=0, ΔG for the HCl reaction is much more negative than for acetic acid. This is summarized in table below. The direction of the arrow shows if products (-->) or reactants (<---) are favored. The size of the arrow shows very approximately to what extent the ΔG term is favored
| Reaction at t=0 | ΔGo | RTln Q | ΔG |
| HCl(aq) + H2O(l) | ---------------> | ---------------> | -----------------------------> |
| CH3CO2H(aq) + H2O(l) | <------------- | ---------------> | -> |
Now when equilibrium is reached, no net change occurs in the concentration of reactants and products, and ΔG = 0. In the case of HCl, there is just an infinitesimal amount of HCl left, and 0.1 M of each product, so concentration favors HCl formation. However, the intrinsic relative stability of reactants and products still favors products. In the case of acetic acid, most of the acetic acid remains (0.099 M) with little product (0.001 M) so concentration favors product. However, the intrinsic relative stability of reactants and products still favors reactants. This is summarized in table below.
| Reaction at equlib. | ΔGostab | RTln Q | ΔG |
| HCl(aq) + H2O(l) | ---------------> | <--------------- | favors neither, = 0 |
| CH3CO2H(aq) + H2O(l) | <------------- | --------------> | favors neither, = 0 |
Compare the two tables above (one at time t= 0 and the other at equilibrium). Notice:
- ΔGonever changes, since it has nothing to do with concentration.
- Only RTln Q changes during the course of a reaction, until equilibrium is achieved.
Meaning of ΔGo
To get a better meaning of the significance of ΔGo, let's consider the following equations under two different conditions:
ΔG = ΔGo + RTln Q = ΔGo + RTln ([P][Q])/([A][B])
Condition I: Reaction at equilibrium, DG = 0
The equation reduces to: ΔGo = - RTln ([P]eq[Q]eq)/([A]eq[B]eq) or ΔGo = - RTln Keq = - 2.303RTlog Keq
This supports our idea that DGo is independent of concentration since Keq should also be independent of concentration.
Condition II: Concentration of all reactants and products is 1 M (standard state, assuming solution reaction)
The equation reduces to: ΔG = ΔGo + RTln ([1][1])/([1][1]) = ΔGo + 2.303RTlog 1 = ΔGo
The implies that when all reactants are at this concentration, defined as the standard state (1 M for solutes), the ΔG at that particular moment just happens to be the DGo for the reaction. If one of the reactant or products is H3O+, it would make little biological sense to calculate DGo for the reaction using the standard state of [H3O+] = 1 M, or a pH of -1. Instead, it is assumed the pH = 7, [H3O+] = 10-7 M. A new symbol is used for DGo under these condition, ΔGo'.
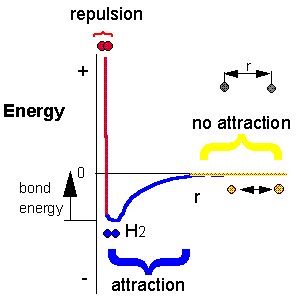
H + H --> H2 Does this reaction occur spontaneously? It does. You should remember that individual H atoms are unstable, since they don't have an completed outer shell of electrons - in this case a duet. As they approach, they can interact to form a covalent bond and in the process release energy. The bonded state is a lower energy state than two separated H atoms. This should be clear since energy has to be added to a molecule of H2 to break the bond.
`
2C8H18(l) + 25O2(g) --> 16CO2(g) + 18H2O(g). To carry out this reaction, every C-C, C-H and O-O bond in the reactants must be broken (which requires an input of energy) but a lots of energy is released on formation of C-O and H-O covalent bonds in the products. Is more energy needed to break the bonds in the reactants or is more energy released on formation of bonds in the product? The answer should be clear. The products must be at a lower energy than the reactants since huge amounts of heat and light energy are released on combustion of gasoline and other hydrocarbons.
These reactions suggest that energy must be released for a reaction to proceed to any extent in a given direction.
Now consider, however, the following reaction:
Ba(OH)2.8H2O(s) + 2NH4SCN(s) --> 10H2O(l) + 2NH3(g) + Ba(SCN)2(aq+s)
When these two solids are mixed, and stirred, a reaction clearly takes places, as evidenced by the formation of a liquid (water) and the smell of ammonia. What is surprising is that heat is not released into the surroundings in this reaction. Rather heat was absorbed from the surroundings turning the beaker so cold that it freezes to a piece of wood (with a layer of water added to the wood) on which it was placed. This reaction seems to violate our idea that a reaction proceeds in a direction in which heat is liberated. Reactions which liberate heat and raise the temperature of the surroundings are called exothermic reactions. Reactions which absorb heat from the surroundings and hence lower the temperature of the surroundings are endothermic reactions.


