8.7: Appendix - Felsenstein's Pruning Algorithm
- Page ID
- 21782
Felsenstein’s pruning algorithm (1973) is an example of dynamic programming, a type of algorithm that has many applications in comparative biology. In dynamic programming, we break down a complex problem into a series of simpler steps that have a nested structure. This allows us to reuse computations in an efficient way and speeds up the time required to make calculations.
The best way to illustrate Felsenstein’s algorithm is through an example, which is presented in the panels below. We are trying to calculate the likelihood for a three-state character on a phylogenetic tree that includes six species.
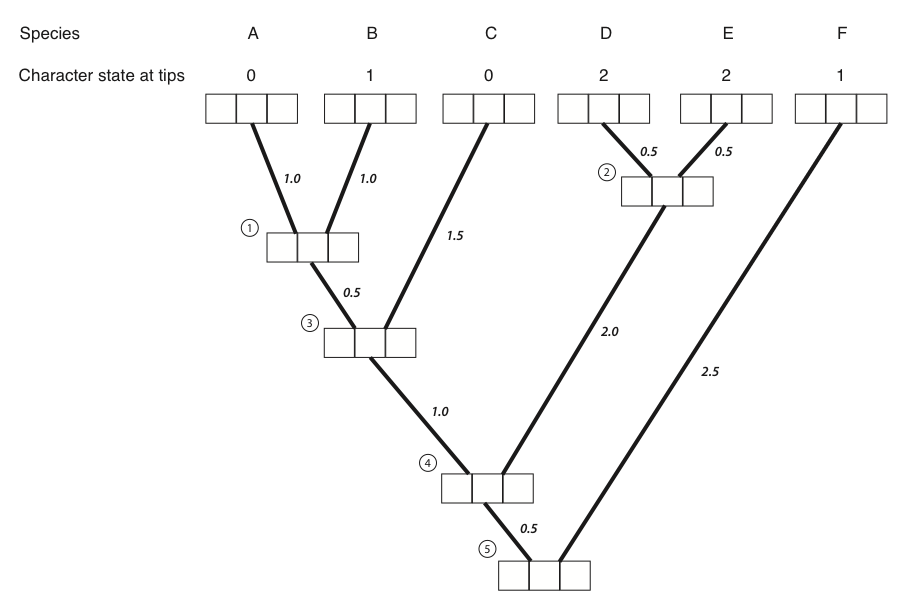
Figure 8.4A. Each tip and internal node in the tree has three boxes, which will contain the probabilities for the three character states at that point in the tree. The first box represents a state of 0, the second state 1, and the third state 2. Image by the author, can be reused under a CC-BY-4.0 license.
- The first step in the algorithm is to fill in the probabilities for the tips. In this case, we know the states at the tips of the tree. Mathematically, we state that we know precisely the character states at the tips; the probability that that species has the state that we observe is 1, and all other states have probability zero:
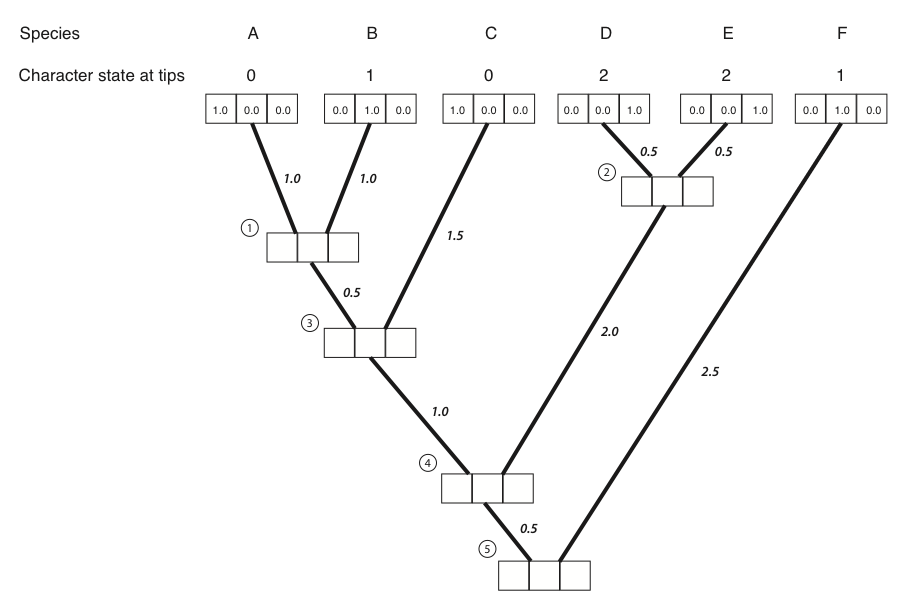
- Next, we identify a node where all of its immediate descendants are tips. There will always be at least one such node; often, there will be more than one, in which case we will arbitrarily choose one. For this example, we will choose the node that is the most recent common ancestor of species A and B, labeled as node 1 in Figure 8.2B.
- We then use equation 7.6 to calculate the conditional likelihood for each character state for the subtree that includes the node we chose in step 2 and its tip descendants. For each character state, the conditional likelihood is the probability, given the data and the model, of obtaining the tip character states if you start with that character state at the root. In other words, we keep track of the likelihood for the tipward parts of the tree, including our data, if the node we are considering had each of the possible character states. This calculation is:
\[ L_P(i) = (\sum\limits_{x \in k}Pr(x|i,t_L)L_L(x)) \cdot (\sum\limits_{x \in k}Pr(x|i,t_R)L_R(x)) \label{8.7}\]
where i and x are both indices for the k character states, with sums taken across all possible states at the branch tips (x), and terms calculated for each possible state at the node (i). The two pieces of the equation are the left and right descendant of the node of interest. Branches can be assigned as left or right arbitrarily without affecting the final outcome, and the approach also works for polytomies (but the equation is slightly different). Furthermore, each of these two pieces itself has two parts: the probability of starting and ending with each state along the two branches being considered, and the current conditional likelihoods that enter the equation at the tips of the subtree (LL(x) and LR(x)). Branch lengths are denoted as tL and tR for the left and right, respectively.
One can think of the likelihood "flowing" down the branches of the tree, and conditional likelihoods for the left and right branches get combined via multiplication at each node, generating the conditional likelihood for the parent node for each character state (LP(i)).
Consider the subtree leading to species A and B in the example given. The two tip character states are 0 (for species A) and 1 (for species B). We can calculate the conditional likelihood for character state 0 at node 1 as:
\[ L_P(0) = \left(\sum\limits_{x \in k}Pr(x|0,t_L=1.0)L_L(x)\right) \cdot \left(\sum\limits_{x \in k}Pr(x|0,t_R=1.0)L_R(x)\right) \label{8.8}\]
Next, we can calculate the probability terms from the probability matrix P. In this case tL = tR = 1.0, so for both the left and right branch:
\[ \mathbf{Q}t = \begin{bmatrix} -2 & 1 & 1 \\ 1 & -2 & 1 \\ 1 & 1 & -2 \\ \end{bmatrix} \cdot 1.0 = \begin{bmatrix} -2 & 1 & 1 \\ 1 & -2 & 1 \\ 1 & 1 & -2 \\ \end{bmatrix} \label{8.9}\]
So that:
\[ \mathbf{P} = e^{Qt} = \begin{bmatrix} 0.37 & 0.32 & 0.32 \\ 0.32 & 0.37 & 0.32 \\ 0.32 & 0.32 & 0.37 \\ \end{bmatrix} \label{8.10}\]
Now notice that, since the left character state is known to be zero, LL(0)=1 and LL(1)=LL(2)=0. Similarly, the right state is one, so LR(1)=1 and LR(0)=LR(2)=0.
We can now fill in the two parts of equation 8.2:
\[ \sum\limits_{x \in k}Pr(x|0,t_L=1.0)L_L(x) = 0.37 \cdot 1 + 0.32 \cdot 0 + 0.32 \cdot 0 = 0.37 \label{8.11} \]
and:
\[ \sum\limits_{x \in k}Pr(x|0,t_R=1.0)L_R(x) = 0.37 \cdot 0 + 0.32 \cdot 1 + 0.32 \cdot 0 = 0.32 \label{8.11B} \]
So:
LP(0)=0.37 ⋅ 0.32 = 0.12.
This means that under the model, if the state at node 1 were 0, we would have a likelihood of 0.12 for this small section of the tree. We can use a similar approach to find that:
(eq. 8.13)
LP(1)=0.32 ⋅ 0.37 = 0.12.
LP(2)=0.32 ⋅ 0.32 = 0.10.
Now we have the likelihood for all three possible ancestral states. These numbers can be entered into the appropriate boxes:
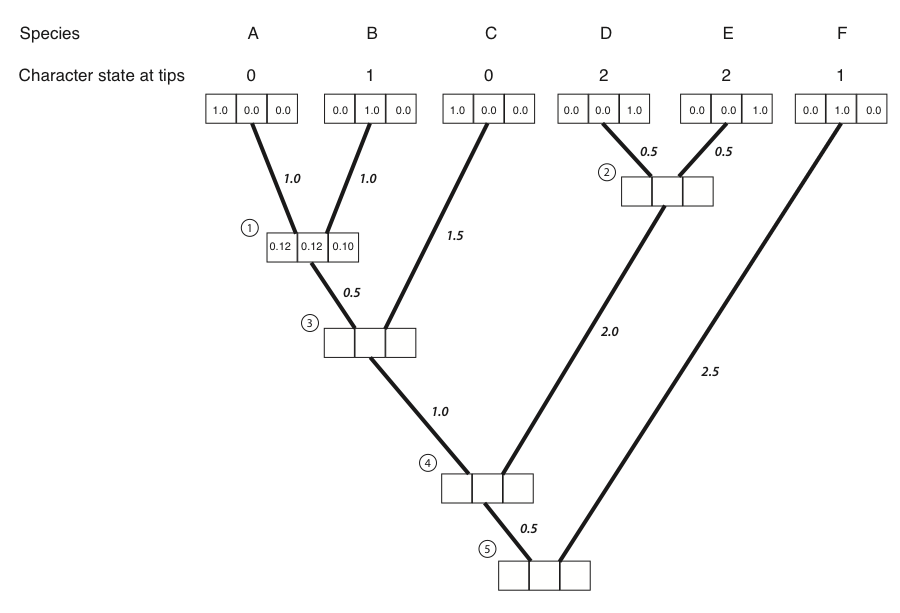
- We then repeat the above calculation for every node in the tree. For nodes 3-5, not all of the LL(x) and LR(x) terms are zero; their values can be read out of the boxes on the tree. The result of all of these calculations:
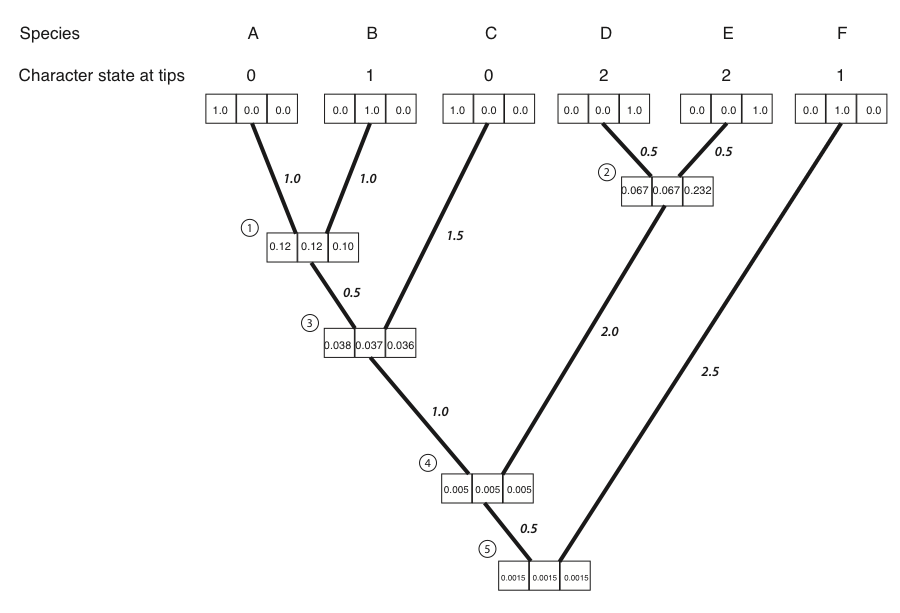
- We can now calculate the likelihood across the whole tree using the conditional likelihoods for the three states at the root of the tree.
\[ L = \sum\limits_{x \in k} \pi_x L_{root} (x) \label{8.14}\]
Where πx is the prior probability of that character state at the root of the tree. For this example, we will take these prior probabilities to be uniform, equal for each state (πx = 1/k = 1/3). The likelihood for our example, then, is:
\[L = 1/3 ⋅ 0.00150 + 1/3 ⋅ 0.00151 + 1/3 ⋅ 0.00150 = 0.00150 \label{8.15}\]
Note that if you try this example in another software package, like GEIGER or PAUP*, the software will calculate a ln-likelihood of -6.5, which is exactly the natural log of the value calculated here.

