D. The System, Surroundings, and the Universe - Laws of Thermodynamics
- Page ID
- 4676
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)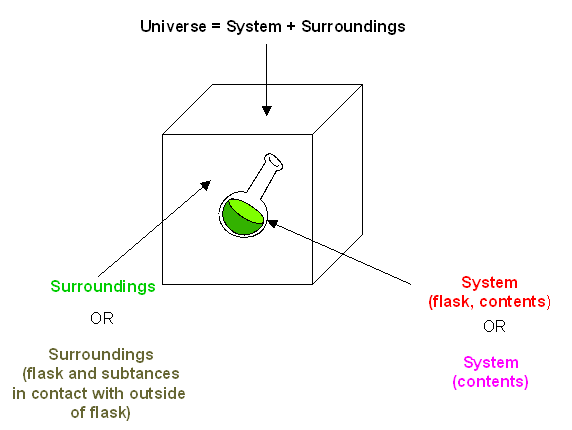
You may remember from General Chemistry that the change in the internal energy of a system, ΔE, is given by:
ΔEsys = q + w = q - PextΔV
where q is the heat (thermal energy) transferred to the system (+), from the system (-), w is the work done on (+) or by (-) the system. If only PV work is done, w = - PextΔV, where Pext is the external pressure resisting a volume change in the system, ΔV. When pressure is constant, and only PV work is done,
qp = ΔEsys + PextΔV = ΔH,
where qp is the heat transferred at constant P (easily measured in a coffee cup calorimeter) which is equal to the change in enthalpy, ΔH, of the system. For exothermic reactions, the reactants have more thermal energy than the products, and the heat energy (measured in kilocalories) released is the difference between the energy of the products and reactants. When heat energy is used to measure the difference in energy, we call the energy enthalpy (H) and the heat released as the change in enthalpy (ΔH), as illustrated below.
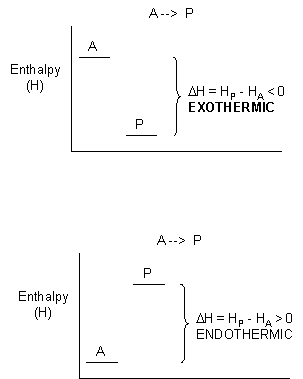
For exothermic reactions, ΔH < 0. For endothermic reactions, ΔH > 0.
The equation ΔEsys = q + w = q - PextΔV is one expression of the First Law of Thermodynamics. Another, a statement of energy conservation, is:
ΔEtot = ΔEuniverse = ΔEsys + ΔEsurr.= 0.
Clearly, there must be something more that decides whether a reaction goes to a significant extent other that if heat is released from the system. That is, the spontaneity of a reaction must depend on more than just ΔHsys. . Another example of a spontaneous natural reaction is the evaporation of water (a physical, not chemical process).
H2O (l) --> H2O (g)
Heat is absorbed from the surroundings to break the intermolecular forces (H bonds) among the water molecules (the system), allowing the liquid to be turned into a gas. If the surroundings are the skin, evaporation of water in the form of sweat cools the body. What are these reactions spontaneous and essentially irreversible even though they are endothermic? Notice that in both of these endothermic reactions (the reactions of Ba(OH)2.8H2O(s) and 2NH4SCN(s) and the evaporation of water), the products are more disorganized (more disordered) than the products. A solid is more ordered than a liquid or gas, and a liquid is more ordered than a gas. In nature, ordered things become more disordered with time. Entropy (S), the other factor (in addition to enthalpy changes) is often considered to be a measure of the disorder of a system. The greater the entropy, the greater the disorder. For reactions that go from order (low S) to disorder (high S), the changed in S, ΔS > 0. For reaction that goes from low order to high order, ΔS < 0.
However, this common description of entropy is quite misleading. Macroscopic examples describing order/disordered states (such as the cleanliness of your room or the shuffling of a deck of card) are inappropriate since entropy deals with microscopic states.
The driving force for spontaneous reactions is the dispersion of energy and matter. Increases in entropy for reactions that involve matter occur when gases or solutes in solution are dispersed, leading to increases in positional entropy. For reactions involving energy changes, entropy increases when energy is dispersed as random, undirected thermal motion, leading to increases in thermal entropy. In this sense, entropy, S (a measure of
("spreadedness") is a measure of number of different ways (microstates) that particles or energy can be arranged (W), not a measure of disorder! W is an abbreviation for the German word, Wahrscheinlichkeith, which means probabilty. It can be shown that for a solute dissolving in a solvent, Wsys = Wsolute x Wsolvent. Note that this is a multiplicative function. Entropy is a logarithmic function of W which allows additivity of solute and solvent W values, a feature found in other thermodynamic state functions like ΔE, ΔH, and ΔS. Hence ln Wsys = ln Wsolute + ln Wsolvent. Boltzman showed that
S = k ln W where k is the Boltzman constant (1.68 x 10-23 J/K), S units: J/Kfor molecules, or
S = kNA ln W = RlnW (J/K.mol) for moles of molecules.
Boltzman realized the connection between the macroscopic entropy of a system and the microscopic order/disorder of a system through the equation S = klnW, Increasing S (macroscopic property) occurs with increasing numbers of possible microscopic states for the atoms and molecules of a system.
The dissolution of a solute in water and the expansion of a gas into a vacuum, both which proceed spontaneously toward an increase in matter dispersal, are examples of familiar processes characterized by a ΔSsys > 0.
The spontaneity of exothermic and endothermic processes will depend on the DStot = DSsurr + DSsys. DSsys often depends on matter dispersal (positional entropy). DSsurr depends on energy changes in the surroundings, ΔHsurr = -ΔHsys(thermal entropy).
It is more convenient to express thermodynamic properties based on the system which is being studied, not on the surrounding. This can be readily done for the ΔSsurr which depends both on ΔHsys and the temperature. First consider the dependency on ΔHsys. thermal energy flow into or out of the system, and since ΔHsys = - ΔHsurr,
ΔSsurr a -ΔHsys
For an exothermic reaction, ΔSsurr > 0 (since ΔHsys < 0) and the reaction is favored;
For an endothermic reaction, ΔSsurr < 0, (since ΔHsys > 0), and the reaction is disfavored;
ΔSsurr also depends on the temperature T of the surroundings:
ΔSsurr a 1/T
If the Tsurr is high, a given heat transfer to or from the surroundings will have a smaller effect on the ΔSsurr; conversely, if the Tsurr is low, the effect on ΔSsurr will be greater. (Atkins, in his recent General Chemistry, uses the analogy of the effect of a sneeze in library compared to in a crowded street; The new American Chemistry General Chemistry text uses the analogy of giving $5 to a friend with $1000 compared to one who has just $10.) Hence,
ΔSsurr = -ΔHsys/T (Note: from a more rigorous thermodynamic approach, entropy can be determined from dS = dqrev/T.)
DStot = DSsurr + DSsysΔStot depends on both enthalpy changes in the system and entropy changes in the surroundings.
DStot = - DHsys/T + DSsys Multiplying both sides by -T gives -TΔStot = ΔHsys + TΔSsys The thermodynamic function Gibb's Free Energy, G, can be defined as: G = H - TS;At constant T and P, ΔG = ΔH - TΔS
Hence ΔGsys = ΔHsys - TΔSsys = - TΔStot Spontaneity is determined by ΔStot OR ΔGsys since ΔStot = -ΔGsys/T . ΔGsys is widely use in discussing spontaneity since it is a state function, depends only on the enthalpy and entropy changes in the system, and is negative (as is the potential energy change for a falling object) for all spontaneous processes.The second law of thermodynamics can be succinctly stated: For any spontaneous process, the ΔStot > 0. Unlike energy (from the First Law), entropy is not conserved.


