6.2: Kinetics without Enzymes
- Page ID
- 21141
Single Step Reactions
First, we will explore the kinetics of non-catalyzed reactions, which is needed to understand the kinetic of the more complicated enzyme-catalyzed reactions.
In this book, we will refer to the change of concentration of a chemical species X as a function of time as dX/dt instead of ΔX/Δt, where dX/dt is the derivative of X with respect to time t. This is the language of calculus, which most readers would have studied. The use of calculus will be mainly limited to writing equations of the form dX/dt = f(t), which is a type of differential equation. We will also use a few integrals, but a working knowledge of calculus is not required. For readers who have not studied calculus, replace dX/dt with ΔX/Δt in your mind, and you will derive the same meaning.
You studied two types of kinetic equations in introductory chemistry to analyze kinetic data:
- Initial Rates: In this method, the initial rate, v0, is measured as a function of the concentration of reactants. The initial velocity, v0, is the initial slope of a graph of the concentration of reactants or products as a function of time, taken over a range of times such that only a small fraction of A has reacted. Under this condition, [A] over this short time range is approximately constant and equal to Ao. Initial rate graphs are often based on the measurement of product increase with time, ΔP/Δt, so v0 vs. A plots have positive slopes. The velocity at time t along the A vs. t curve, dA/dt, constantly changes as [A] decreases since the velocity depends on the [A]. To reiterate, the initial velocity of the reaction is the slope of the initial linear part of the decay curve when the rate is essentially linear over a narrow range of [A].
- Integrated Rates and Progress Curves: In this method, a differential equation that gives the change of A or P with time (dA/dt or dP/dt) is integrated to give an equation that shows the concentration of A or P as a function of time. For any given reaction, it is essential to be able to write the integrated rate equation, often called an ordinary differential equation (ODE). In almost every case, we provide the solutions to the ODEs in either a mathematical equation or a fitted graph of A vs. t. As the reactions get more complicated, we let computers solve them numerically and show the output. The ODEs are also called progress curves as they show how the concentration of reactants and products change with time.
In either case, the mathematical equations describing the reaction are used to fit experimental data taken in the lab. Statistics are used to see how closely the experimental data fit the rate equations. The best-fit equation give the mostly likely chemical reaction equations for the interconversion of reactant and products.
Most biochemistry textbooks focus on initial velocities when explaining enzyme kinetics. However, in many ways, this method is less intuitive than exploring how the concentration of a molecule changes with time. An analogy is the concept of density (mass/volume), which is more complicated than understanding mass or volume separately. We use both methods to develop both chemical and biological intuitions of kinetic properties.
We will first explore simple irreversible reactions (1st and 2nd order), then make them reversible, and then couple them together to form more complex reaction schemes, much as we are compelled to do for enzyme-catalyzed reactions.
First Order Reaction
\[\ce{A ->[k_{1}] P} \nonumber \]
where k1 is the first-order rate constant. For these reactions, the velocity of the reaction, \(v\), is directly proportional to [A], or
\[v=-\frac{d A}{d t}=+\frac{d P}{d t}=k_{1} A \label{6.3.A.1} \]
The negative sign in -d[A]/dt indicates that the concentration of A decreases. The equation could also be written as:\(v=\frac{d A}{d t}=-k_{1} A\)
For the rest of the reactions in this book, we follow the convention of writing all velocities expressed as d[x]/dt as positive numbers. A negative sign for a term on the right-hand side of the differential equation will indicate that the concentration dependency of that term will lead to a decrease in [x] with time. Likewise, a positive sign for the term on the right-hand side of the equation will indicate that concentration dependency of that term will lead to an increase in [x] with time.
Examples: dA/dt = -kA shows that the A will decrease with time. dA/dt = +kA shows that A will increase with time.
Here is the solution to the differential Equation 6.3.A.1 for [A] as a function of t.
\begin{equation}
A=A_0 e^{-k_1 t}
\end{equation}
Here it is!
- Derivation
-
\begin{equation}
\begin{gathered}
\int_{A_O}^A \frac{d A}{A}=-k_1 \int_0^t d t \\
\ln A-\ln A_0=-k_1 t \\
\ln A=\ln A_0-k_1 t \\
A=A_0 e^{-k_1 t}
\end{gathered}
\end{equation}
Equation 6.3.A.2 is an example of an integrated rate equation. The following graphs show plots o.f A vs t and lnA vs. t for a first-order process. Note that the derivative of the graph of A vs. t (dA/dt) is the velocity of the reaction. The graph of ln[A] vs. t is linear with a slope of -k1. The velocity of the reaction (slope of the A vs t curve) decreases with decreasing A, which is consistent with equation 1. Again, the initial velocity is determined from data taken in the first part of the decay curve when the rate is linear and little A has reacted. That is, [A] is approximately equal to [A0].
Figure \(\PageIndex{1}\) shows two ways to plot 1st order reaction data. The left graph shows the exponential decay of A with time and the corresponding rise in P when A0 is 0 and k1=2. The other shows the linear fall of ln[A] vs time.
|
Once again, for complete clarification, another way of analyzing the kinetics of a reaction, in addition to following the concentration of a reactant or product as a function of time and fitting the data to an integrated rate equation, is to plot the initial velocity, vo, of the reaction as a function of the concentration of reactants. The initial velocity is the initial slope of a graph of the concentration of reactants or products as a function of time, taken over a range of times such that only a small fraction of A has reacted, so [A] is approximately constant = Ao. From the first-order graph of A vs. t above, the slope approaches 0 with increasing time as [A] approaches 0, which indicates that the reaction velocity depends on A. For this first-order order process, two equivalent equations can be written showing the
Both equations show that v is directly proportional to A. As [A] is doubled, the initial velocity is doubled. Velocity graphs used by biochemists often show the initial velocity of product formation (not reactant decrease) as a function of reactant concentration. Hence, as product concentration increases, the initial velocity are positive. A graph of v (= dP/dt) vs [A] for a first order process would have a positive slope and be interpreted as showing that the rate of appearance of P depends linearly on [A]. |
Second Order/Pseudo First Order Reactions
\begin{equation}
A+B \stackrel{k_2}{\longrightarrow} P \text { or } A+A \stackrel{k_2}{\longrightarrow} P
\end{equation}
where \(k_2\) is the second-order rate constant. For the first of these irreversible reactions, the velocity of the reaction, v, is directly proportional to [A] and [B], or
\begin{equation}
v=\frac{d A}{d t}=-k_2[A][B]
\end{equation}
We will consider two special cases of this reaction type:
- [B] >> [A]. Under these conditions, [B] never changes, so Equation 5 becomes
\begin{equation}
v=-\left(k_2[B]\right)[A]=-k_1^{\prime}[A]
\end{equation}
where k1' is the pseudo first order rate constant (= k2[B] ) for the reaction. The reaction appears to be first order, depending only on [A].
- As illustrated in the second reaction above, the only reactant is A, which must collide with another A to form P.
The following differential equation can be written and solved to find [A] as a function of t.
\begin{equation}
v=\frac{d A}{d t}=2 \frac{d P}{d t}=-k_2 A^2
\end{equation}
Solving the differential equation for A gives the following:
\begin{equation}
\frac{1}{A}=\frac{1}{A_0}+k_2 t
\end{equation}
Here it is!
- Derivation
-
\begin{equation}
\begin{gathered}
\frac{d A}{d t}=-k_2 A^2 \\
\int_{A_0}^A \frac{d A}{A^2}=\int_{A_0}^A A^{-2} d A=\int_{A_0}^A A^{-2} d A=-k_2 \int_0^t d t \\
\left.\left.\left.\frac{A^{n+1}}{n+1}\right]_{A_0}^A=\frac{A^{-1}}{-1}\right]_{A_0}^A=-k_2 t\right]_{A_0}^A \\
-\frac{1}{A}-\left(\frac{1}{A_0}\right)=-k_2 t
\end{gathered}
\end{equation}
Figure \(\PageIndex{2}\) shows plots of A vs. t and 1/A vs. t for a second-order process when A0 is 0 and k2=1. The right graph shows the linear rise of 1/[A] with time.
Note that just from a plot of A vs. t, it would be difficult to distinguish a first from a second-order reaction. If the plots were superimposed, you would observe that at the same concentration of A (10, for example), the vo of a first-order reaction would be proportional to 10, but for a second-order reaction, to 102 or 100. Therefore, the second-order reaction is faster (assuming similarity in the relative magnitude of the rate constants), as indicated by the steeper negative slope of the curve. However, at low A (0.1 example), the vo of a first-order reaction would be proportional to 0.1 but second-order order reaction to 0.12 or 0.01. Therefore, at low A, the second-order reaction is slower.
The interactive graphs below show the first and second-order conversion of reactant A to product. Change the sliders to see how the curves are different.
By comparing these curves, you should see how difficult it is to differentiate between a 1st and 2nd order process unless the reaction progresses to almost completion.
Multi-Step Reactions
Reversible First Order Reactions
\begin{equation}
\mathrm{A} \underset{\mathrm{k}_2}{\stackrel{\mathrm{k}_1}{\rightleftarrows}} \mathrm{P}
\end{equation}
Here is the differential equation for dA/dt..
\begin{equation}
\mathrm{v}=\frac{\mathrm{dA}}{\mathrm{dt}}=-\mathrm{k}_1 \mathrm{~A}+\mathrm{k}_2 \mathrm{P}
\end{equation}
Here are the solution for both A and P as a function of time
\begin{equation}
\begin{gathered}
\mathrm{A}=\frac{\mathrm{A}_0\left(\mathrm{k}_2+\mathrm{k}_1\left[\mathrm{e}^{-\left(\mathrm{k}_1+\mathrm{k}_2\right) \mathrm{t}}\right]\right.}{\mathrm{k}_1+\mathrm{k}_2} \\
\mathrm{P}=\mathrm{A}_0-\left(\frac{\mathrm{A}_0\left(\mathrm{k}_2+\mathrm{k}_1\left[\mathrm{e}^{-\left(\mathrm{k}_1+\mathrm{k}_2\right) \mathrm{t}}\right]\right.}{\mathrm{k}_1+\mathrm{k}_2}\right)
\end{gathered}
\end{equation}
Figure \(\PageIndex{3}\) shows graphs of A and P vs t for this reaction at two different sets of values of k1 and k2.
Change the sliders on the interactive graph below of a reversible reaction to see how changing the relative values of the forward and reverse rate constants affects the concentrations at which the concentration plateaus are reached.
We all grew up on mathematical graphs that give you valuable insight into textual descriptions and data tables from which the graphs were made. These graphs are enhanced when you can use sliders to change constants as for the reversible reaction A ↔ P above. Even then, you might not infer that when the reaction has reached equilibrium, product is still being made from reactant, and reactant from product, since the equilibrium is dynamic. To add insight into simple and complex reactions, animations showing the continual disappearance of reactants and products are valuable.
This book will incorporate many animations to visually show the changes in the reactant and product concentrations. Hui Liu and Shraddha Nayak (Animation Lab, University of Utah) made all the animations in this book using mathematical solutions to the progress curves for the reactions. Multiple modes of presentation are useful as learners with different backgrounds and preferred ways of learning attempt to understand complex materials.
It is relatively simple to write the differential equations (differential) to show how the rate of disappearance of a reactant A (for example), dA/dt, depends on the concentration of its immediate participants in the reaction. It is not so easy to solve the equations (as we did above) for the progress curve, which shows how [A] changes with time t (i.e. [A] = f(t)). Luckily, many programs have been developed that produce numerical solutions to the differential equations and give progress curve graphs like [A] = f(t). Two interrelated, freely available programs, Copasi and Virtual cell (Vcell), can solve all the equations for hundreds of cellular reactions simultaneously. They use a format called Systems Biology Markup Language (SBML) for describing and storing computational models. We will use Vcell models in this book as they are straightforward to create. All the coding to describe the reactions is built into Vcell and this book and hidden from you. All you will see are the output results. You can change the progress curves by moving sliders to change constants and see the resulting changes in graphical outputs.
The VCell models use a reaction diagram that shows all of the interconnected species. The first Vcell model we will run is for the reversible conversion of A to P (A ↔P), which we just discussed and displayed in the graph above. Here is the Vcell reaction diagram and a description of its components.
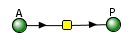
- The reactant A and product P are called species and are shown as green spheres.
- The yellow square indicates a reaction node connecting A to P.
- Lines connect the species that participate in the reaction. The arrows appear unidirectional, BUT the equations describing the concentrations of A and P are derived assuming a reversible reaction with rate constants kf (forward reaction) and kr (reverse reaction).
The program calculates A and P as a function of time (i.e. it solves the differential equations for both species). The graphs of concentration vs time are called progress curves. It also can calculate fluxes (J) (velocities) for each species. The flux at any given time is the slope of the concentration vs time curve at any given time. When we get to metabolism, we will talk about fluxes of metabolites through pathways. Also, fluxes are used to describe the rate of movement of solute through membranes. Here is the result of the simulation run in Vcell, exported as a sbml file, and displayed in the book using a program called MiniSideWinder.
MODEL
Animations
The video animations show particles representing A (red) and P (cyan) interconverting in a reversible process with embedded progress curves showing A (red) and P (cyan) vs. time.
| Reversible Rx A (red) ↔ B (cyan): kF = kR = 3 | Reversible Rx A (red) ↔ B (cyan): kF=4, kR=2 | Reversible Rx A (red) ↔ B (cyan): kF=2, kR=4 |
 |
 |
 |
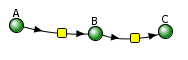
Consecutive Irreversible First Order Reactions
![]()
The following differential equations can be written for these reactions:
\begin{equation}
\begin{gathered}
\frac{\mathrm{d} \mathrm{A}}{\mathrm{dt}}=-\mathrm{k}_1 \mathrm{~A} \\
\frac{\mathrm{dB}}{\mathrm{dt}}=\mathrm{k}_1 \mathrm{~A}-\mathrm{k}_2 \mathrm{~B} \\
\frac{\mathrm{dC}}{\mathrm{dt}}=\mathrm{k}_2 \mathrm{~B}
\end{gathered}
\end{equation}
Here are the solutions to the differential equations:
\begin{array}{c}{\mathrm{A}=\mathrm{A}_{0} \mathrm{e}^{-\mathrm{k}_{1} \mathrm{t}}} \\ {\mathrm{B}=\frac{\mathrm{k}_{1} \mathrm{A}_{0}}{\mathrm{k}_{2}-\mathrm{k}_{1}}\left(\mathrm{e}^{-\mathrm{k}_{1} \mathrm{t}}-\mathrm{e}^{-\mathrm{k}_{2} \mathrm{t}}\right)} \\ {\mathrm{C}=\mathrm{A}_{0}-\mathrm{A}-\mathrm{B}=\mathrm{A}_{0}\left[1+\frac{1}{\mathrm{k}_{1}-\mathrm{k}_{2}}\left(\mathrm{k}_{2} \mathrm{e}^{-\mathrm{k}_{1} \mathrm{t}}-\mathrm{k}_{1} \mathrm{e}^{-\mathrm{k}_{2} \mathrm{t}}\right]\right.}\end{array}
Figure \(\PageIndex{4}\) shows graphs of A, B, and C vs. t for these reactions for a fixed value of k1 and k2.
Figure \(\PageIndex{4}\): Graphs of A, B, and C vs. t for the irreversible reactions A → B → C for a fixed value of k1 and k2.
Change the sliders on the interactive graph below to see how changing the forward and reverse rate constants affect the curves.
Here are two different animations for the irreversible reaction using different rate constants.
| Irreversible Rx A (red) → B (cyan) → C (blue) k1 = 0.2, k2 = 0.6 |
Irreversible Rx A (red) → B (cyan)→ C (blue) k1= 0.6, k2 = 0.2 |
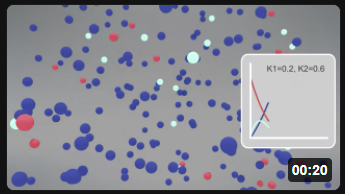 |
 |
Consecutive Reversible First Order Reactions
You can imagine that solving the equations for the completely reversible reactions of A ↔ B ↔ C would be very difficult. However, writing the differential equations for each step is straight-forward and can be done easily in Vcell by choosing the built-in equations for each separate reaction based on mass action. The program can then solve the equations numerically to produce progress curve graphs.
Now let's look at the simulation for the fully reversible reactions A ↔ B ↔ C. Again, the model was built and solve in VCell, and then exported in the system's biology markup language (sbml) format. The interactive graphs are made using a program called miniSideWinder.
A note: Arrows in VCell Diagrams - In the reaction diagram for the reversible reaction A ↔ B ↔ C below, the arrows go in only one direction, left to right, and simply show that the species are connected. However, in the Vcell program, the equations for the reversible reaction were used to produce the graphs below. To run the simulation of the irreversible reaction, the rate constants for the reverse reaction would be set to 0.
MODEL
Here is the corresponding animation for the fully reversible reaction A ↔ B ↔ C.
| Reversible Rx A (red) ↔ B (cyan) ↔ C Blue) k1f = 0.2, k1r = 0.1; k2f =0.6, k2r = 0.3 |
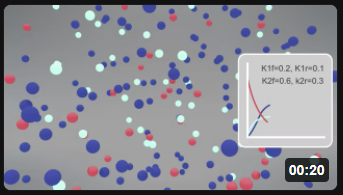 |