4.12: Laboratory Determination of the Thermodynamic Parameters for Protein Denaturation
- Page ID
- 69626
Introduction
Multiple methods can be used to investigate the denaturation of a protein. These include UV, fluorescence, CD, and viscosity measurement. In all these methods the dependent variable (y) is measured as a function of the independent variable, which is often temperature (for thermal denaturation curves) or denaturant (such as urea, guanidine hydrochloride) concentration. From these curves, we would like to calculate the standard free energy of unfolding (ΔGO) for the protein (for the reaction N ↔ D). It is relatively to calculate if the denaturation curves show a sigmoidal, cooperative transition from the native to the denatured state, indicating a two-state transition. The dependent variable can also be normalized to show fractional denaturation (fD). An idealized denaturation curve is shown below in Figure \(\PageIndex{1}\).
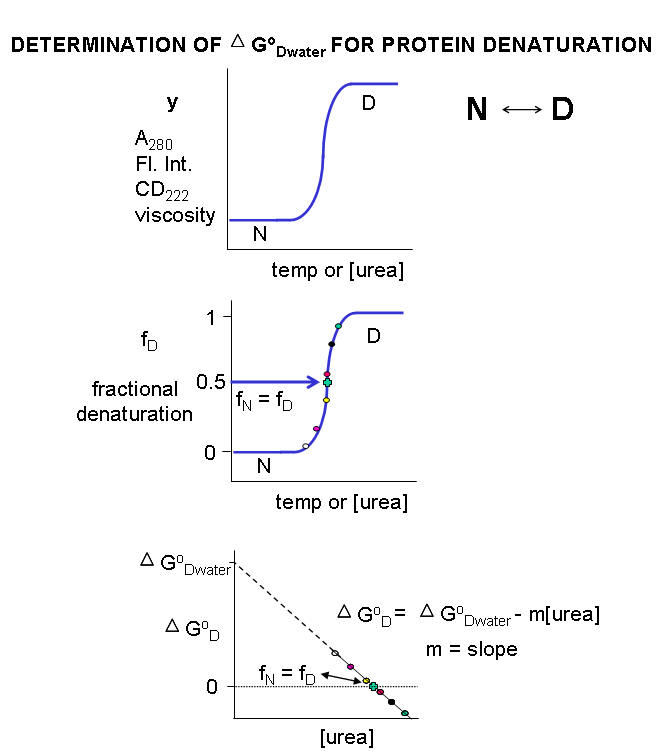
A more realistic denaturation curve might show a small linear change in the dependent variable (fluorescence intensity for example) for temperature or denaturant concentrations well before the major unfolding transition, as well as above those at which it is unfolded. In these cases, the mathematical analyses presented at the end is required.
Denaturation with urea or guanidine hydrochloride
For each curve, the value of \(y\) (either A280, fluorescence intensity, viscosity, etc.) can be thought of as the sum contributed by the native state and from the denatured states, which are both present in different fractional concentrations from 0 - 1. Hence the following equation should be reasonably intuitive.
\[y=\left(f_{N} y_{N}\right)+\left(f_{D} y_{D}\right) \label{1} \]
where \(f_N\) is the fraction native and \(y_N\) is the contribution to the dependent variable \(y\) from the native state, and \(f_D\) is the fraction denatured and \(y_D\) is the contribution to the dependent variable \(y\) from the denatured state. Conservation gives the following equation.
\[1=f_{N}+f_{D} \text { or } f_{N}=1-f_{D} \label{2} \]
Substituting \ref{2} into \ref{1} gives
\[y=\left(1-f_{D}\right) y_{N}+\left(f_{D} y_{D}\right)=y_{N}-f_{D} y_{N}+\left(f_{D} y_{D}\right) \nonumber \]
Rearranging this equation gives
\[\mathrm{f}_{\mathrm{D}}=\frac{\mathrm{y}-\mathrm{y}_{\mathrm{N}}}{\mathrm{y}_{\mathrm{D}}-\mathrm{y}_{\mathrm{N}}} \label{3} \]
Notice the right-hand side of the equations contains variables that are easily measured.
By substituting \ref{2} and \ref{3} into the expression for the equilibrium constant for the reaction \(\ce{N <=> D}\) we get:
\begin{equation}
K_{e q}=\frac{[D]_{e q}}{[N]_{e q}}=\frac{f_D}{f_N}=\frac{f_D}{1-f_D}
\end{equation}
From this, we can calculate ΔG0.
\begin{equation}
\Delta \mathrm{G}^0=-\mathrm{R} \operatorname{Tln} \mathrm{K}_{\mathrm{eq}}=-\mathrm{R} \operatorname{Tln}\left[\frac{\mathrm{f}_{\mathrm{D}}}{1-\mathrm{f}_{\mathrm{D}}}\right]
\end{equation}
Remember that ΔGO (and hence Keq) depends only on the intrinsic stability of the native vs denatured state for a given set of conditions. They vary as a function of temperature and solvent conditions. At low temperatures and low urea/guanidine HCl concentration, the native state is favored, and for the N ↔ D transition, ΔGO > 0 (i.e., denaturation is NOT favored). The denatured state is favored at high temperatures and urea/guanidine-HCl concentrations and ΔGO < 0.
At some temperature or urea/guanidine concentration value, both the native and denatured states would be equally favored. At this value, Keq = 1 and ΔGO = 0.
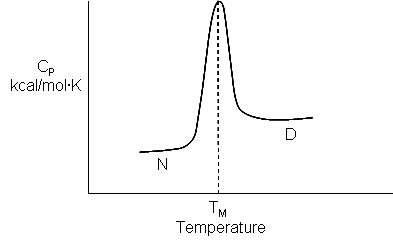
The temperature at this point is called the melting temperature (Tm) of the protein. It is analogous to the Tm in the heat capacity vs temperature graphs for protein denaturation, as we saw in Chapter 4.9. This is Illustrated in Figure \(\PageIndex{2}\).
Ordinarily, at a temperature much below the Tm for the protein or at a low urea concentration, so little of the protein would be in the D state that it would be extremely difficult to determine the protein concentration in the D state. Hence it would be difficult to determine the Keq or ΔGo for the reaction N ↔ D. However, in the range where the protein denatures (either with urea or increasing temperature), it is possible to measure fD/fN.and hence ΔGo at each urea or temperature.
Now we can calculate the ΔGow for N ↔ D in water without urea. For a simple two state N ↔ D, a plot of ΔGo vs [urea] is linear and given by the following equation, which should be evident from (\PageIndex{1}\).
\begin{equation}
\Delta \mathrm{G}^0=\Delta \mathrm{G}_{\mathrm{w}}^0-\mathrm{m}[\text { urea }]
\end{equation}
It is important to know the Keq and ΔG0 for the N ↔ D transition in the absence of urea and under "physiological conditions". A comparison of the calculated values of ΔG0w in the absence of urea for a series of similar proteins (such as those varying by a single amino acid prepared by site-specific mutagenesis of the normal or wild-type gene, would indicate to what extent the mutants were stabilized or destabilized compared to the wild-type protein. ΔG0w for the N ↔ D transition of the protein in the absence of denaturant (i.e in water) can be determined by extrapolating the straight line to [urea] = 0. Admittedly, this is a long extrapolation, but with high-quality data and a high correlation coefficient for the linear regression analysis of the best-fit line, reasonable values can be obtained.
Denaturation with heat
Calculation of ΔHo and ΔSo for N <=>D at room temperature
Keq values can be calculated from thermal denaturation curves in the same way as described above using urea as a denaturant by monitoring change in an observable (spectra signal for example) vs temperature. Knowing Keq, ΔH0, DS0 can be calculated from equation x below since a semi-log plot of lnKeq vs 1/T is a straight line with a slope of - ΔH0R and a y-intercept of + ΔS0/R, where R is the ideal gas constant.
\begin{equation}
\begin{gathered}
\Delta \mathrm{G}^{0}=\Delta \mathrm{H}^{0}-\mathrm{T} \Delta \mathrm{S}^{0}=-\mathrm{RTln} \mathrm{K}_{\mathrm{eq}} \\
\ln \mathrm{K}_{\mathrm{eq}}=-\frac{\Delta \mathrm{H}^{0}-\mathrm{T} \Delta \mathrm{S}^{0}}{\mathrm{RT}} \\
\ln \mathrm{K}_{\mathrm{eq}}=-\frac{\Delta \mathrm{H}^{0}}{\mathrm{RT}}+\frac{\Delta \mathrm{S}^{0}}{\mathrm{R}}
\end{gathered}
\end{equation}
From these equations, it should be evident that all the major thermodynamics constants (ΔG0, ΔH0 and ΔS0 ) for the N ↔ D transition can be calculated from thermal denaturation curves.
Equation (9) below shows that the derivative of equation (8) with respect to 1/T (i.e. the slope of equation 8 plotted as lnKeq vs 1/T) is indeed -ΔH0/R. Equation (9) is the van 't Hoff equation, and the calculated value of the enthalpy change is termed the van 't Hoff enthalpy, ΔH0vHoff.
\begin{equation}
\frac{d \ln \mathrm{K}_{\mathrm{eq}}}{d(1 / \mathrm{T})}=-\frac{\Delta \mathrm{H}^{0}}{\mathrm{R}}=-\frac{\Delta \mathrm{H}_{\mathrm{vHoff}}^{0}}{\mathrm{R}}
\end{equation}
It is useful to compare the van 't Hoff enthalpy, ΔH0vHoff, with the enthalpy change determined directly using differential scanning calorimetry by analyzing a plot of Cp vs T. (Note that the area under the Cp vs T curve as the protein transitions to the unfolded state has units of kcal or kJ. The ΔH0 for the unfolding is inversely proportional to the width of the curve.)
In contrast to the long extrapolation of the ΔG0 vs [urea] to [urea] = 0 to get ΔG0 (the y-intercept) in the absence of urea, which has some physical meaning, extrapolation of the straight line from the van 't Hoff plot from equation 8 to get ΔS0/R, the y-intercept, has little meaning since the 1/T value at the y-intercept is 0, which occurs when T approaches infinity. ΔS0 can be calculated at any reasonable temperature from the calculated value of ΔG0 at that temperature and the calculated ΔH0vHoff.



