B3. Rapid Equilibrium Enzyme-Catalyzed Reactions
- Page ID
- 5099
We have previously derived equations for the reversible binding of a ligand to a macromolecule. Next we derived equations for the receptor-mediated facilitated transport of a molecule through a semipermeable membrane. This latter case extended the former case by the addition of a physical transport step. Now, in what hopefully will seem like deja vu, we will derive almost identical equations for the chemical transformation of a ligand, commonly referred to as a substrate, by an enzyme. Two scenarios will be studied.
- Rapid Equilibrium Assumption: - enzyme E (macromolecule) and substrate S (ligand) concentrations can be determined using the dissociation constant since E, S, and ES are in rapid equilibrium, as we previously used in our derivation of the equations for facilitated transport. Sorry about the switch from A to S in designation of substrate. Biochemists use S to represent the substrate (ligand) but also use A, B, and P and Q to represent reactant and products in the case of multi-substrate and multi-product reactions.
- Steady State Assumption (more general): - enzyme and substrate concentrations are not those determined using the dissociation constant.
Enzyme kinetics experiments, as we will see in the next several chapters, must be used to determine the detailed mechanism of the catalyzed reaction. Using kinetics analyzes you can determine the order of binding/dissociation of substrates and products, the rate constants for individual steps, and clues as the to methods used by the enzyme in catalysis.
Rapid Equilibrium
Consider the following reaction mechanism for the enzyme-catalyzed conversion of substrate \(S\) into product \(P\) (we assume that the catalyzed rate is much greater than the noncatalyzed rate.)
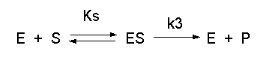
As we did for the derivation of the equations for the facilitated transport reactions under rapid equilibrium conditions, this derivation is based on the assumption that the relative concentrations of \(S\), \(E\), and \(ES\) can be determined by the dissociation constant, \(K_s\), for the interactions and the concentrations of each species during the early part of the reaction (i.e., under initial rate conditions). Assume also the \(S \gg E_o\). Remember that under these conditions, \(S\) does not change much with time. Is this a valid assumption? Examine the mechanism shown above. \(S\) binds to \(E\) with a second order rate constant \(k_1\).
\(ES\) has two fates: it can dissociate with a first order rate constant \(k_2\) to \(S + E\), or it can be converted to product with a first order rate constant of \(k_3\) to give \(P + E\). If we assume that \(k_2 \gg k_3\) (i.e. that the complex falls apart much more quickly than S is converted to P), then the relative ratios of \(S\), \(E\), and \(ES\) can be described by \(K_s\). Alternatively, you can think about it this way. If \(S\) binds to \(E\), most of \(S\) will dissociate, and a small aM_ount will be converted to \(P\). If it does, then \(E\) is now free, and will quickly bind \(S\) and reequilibrate since the most likely fate of bound \(S\) is to dissociate, not be converted to \(P\) (since \(k_3 \ll k_2\)). This also makes sense if you consider that the physical step characterized by \(k_2\) is likely to be quicker than the chemical step, characterized by \(k_3\). Hence the following assumptions have been used:
- \(S \gg E_o\)
- \(P_o = 0\)
- \(k_3\) is rate limiting (i.e., the slowest step)
We would like to derive equations which show the velocity v as a function of the initial substrate concentration, \(S_o\), (assuming that \(P\) is negligible over the time course of measuring the initial velocity). Also assume that the \(v_{catalyzed} \gg v_{noncatalyzed}\). In contrast to the first-order reaction of \(S\) to \(P\) in the absence of E, \(v\) is not proportional to \(S_o\), but rather to \(S_{bound}\) as we described in class with facilitated diffusion (flux proportional to AR, not free A). Therefore,
\[v \propto[ES]\]
or
\[ v = \text{const} \, [ES] = k_3 [ES] \label{1}\]
where \(v\) is the velocity. How can we calculate \([ES]\) when we know \([S]\) (which is equal to \(S_o\)) and Etot (which is \(E_o\))? Let us assume that S is much greater than E, as is the likely biological case. We can calculate \([ES]\) using the following equations and the same procedure we used for the derivation of the binding equation, which gives the equation below:
\[ ES = \dfrac{E_oS}{(K_s + S)} \]
which is analogous to
\[[ML] = \dfrac{M_oL}{K_d + L}\]
Derivation
The dissociation constant can be defined
\[ K_s=\dfrac{[S]_{eq}[E]_{eq}}{[ES]_{eq}} \label{2}\]
and then there is mass balance
\[ [E_o] = [E] + [ES] \label{3}\]
If Equation \(\ref{3}\) is substituted into Equation \(\ref{2}\), we get
\[ K_s = \dfrac{[S]([E_o] - [ES])}{[ES]}\]
which can be expanded to
\[ [ES] K_s = [S][E_o] - [ES][S]\]
or
\[ [ES] K_s +[ES][S] = [S][E_o] \]
and ultimately
\[[ES] = \dfrac{[E_o][S]}{K_s +[S]} \label{4}\]
Substituting Equation \(\ref{4}\) in Equation \(\ref{1}\) give
\[ v = \text{const} [ES] = k_3 [ES] = \dfrac{k_3 [E_o][S]}{K_s + [S]} \]
or
\[ v = \dfrac{V_m [S]}{K_s + [S]} \label{5}.\]
Equation \(\ref{5}\) is the world famous Henri-Michaelis-Menten Equation.
Just as in the case with noncatalyzed first order decay, it is easiest to measure the initial velocity of the reaction when [S] does not change much with time and the velocity is constant (i.e the slope of the \(\frac{dP}{dt}\) curve is constant). A plot of \([P]\) vs. \(t\) (called a progress curve) is made for each different substrate concentration studied. From these curves, the initial rates at each \([S]\) are determined. Alternatively, one set reaction time is determined for all the different substrate concentrations that gives a linear rise in \([P]\) with time. At the time, the reaction can be stopped (quenched) with a reagent that does not cause any change in \(S\) or \(P\). Initial rates can be easily calculated for each \([S]\) from a single data point in this case.
- a plot of \(v\) vs. \(S\) is hyperbolic
- \(v = 0\) when \(S = 0\)
- \(v\) is a linear function of S when \(S \ll K_s\).
- \(v = V_{max}\) or \(V_m\) when \(S\) is much greater than \(K_s\)
- \(S = K_s\) when \(v = \dfrac{V_{max}}{2}\).
These are the same conditions we detailed for our understanding of the binding equation
\[ML = \dfrac{M_oL}{K_d + L} \]
The interactive Mathematics graph below allows you to change the relative value of \(V_m\) and \(K_s\) (which in the graph is given the more general name of \(K_m\)). Note that when \(K_m\) is not \(\ll S\), the graph does not reach saturation and does not look hyperbolic. It should be apparent from the graph that only if \(S \gg K_m\) (or when \(S\) is approximately 100x greater than \(K_m\)) will saturation be achieved.
 Wolfram Mathematica CDF Player - Competitive Inhibition v vs S (free plugin required)
Wolfram Mathematica CDF Player - Competitive Inhibition v vs S (free plugin required)
 History and Picture of Maude Menten
History and Picture of Maude Menten
As we saw in the graph of A or P vs t for a noncatalyzed, first order reaction, the velocity of the reaction, given as the slope of those curves, is always changing. Which velocity should we use in Equation \(\ref{5}\)? The answer invariably is the initial velocity measured in the early part of the reaction when little substrate is depleted. Hence v vs S curves for enzyme catalyzed reactions invariably are really \(v_0\) vs \([S]\).


