C. Molecular Mechanics
- Page ID
- 4667
The following review is based on an NIH Guide to Molecular Modeling, which was removed from the web, to the best of my knowledge, in 1996. I've recreated many of the graphs using Excel.
Molecular mechanics uses Newtonian mechanics to calculate energies of atoms in large molecules like proteins. It assumes that nuclei and electrons are one particle with radii and calculated charged. Bonds are treated as springs connecting atoms. Energies are calculated classically (not with quantum mechanics). Parameters, many based on QM calculations on small molecules, are assigned to all bonds, angles, dihedrals, etc. Interactions are bonded (local) and nonbonded.
Bonded interactions involved atoms connected by one bond (bond stretch), two bonds (angle bending) and 3 bonds (dihedral angle change).
.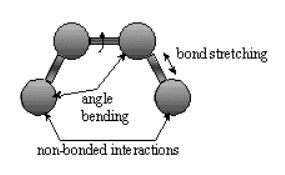
Nonbonded atoms (greater than two bonds apart) interact through van der Waals attraction, steric repulsion and electrostatic attraction/repulsion.
All energy terms from these interactions are summed to give the energy of a given conformation. The energy should be considered relative to those of other conformations. Here is the basic energy equation for all of these energy terms:
\[\mathrm{Energy\: (E) = E_{Stretch} + E_{Bending} + E_{Torsion} + E_\textrm{Non-bonded Interactions}}\]
The "force field" consist of the energy equations and the parameters for each of the energy terms. There are many different commercially available force fields.


