F3. Hydrogen Bonding
- Page ID
- 4766
Linus Pauling first suggested that H bonds (between water and the protein and within the protein itself) would play a dominant role in protein folding and stability. It would seem to make sense since amino acids are dipolar and secondary structure is common. Remember, however, the H bonds would be found not only in the native state but also in the denatured state. Do they contribute differently to the stability of the D vs N states? Many experimental and theoretical studies have been performed investigating helix \(\rightleftharpoons \) (random) coil transitions in small peptides. Remember all the intrachain H bonds in the helix? Are they collectively more stable than H bonds between water and the peptide in a (random) coil?
In thinking about conformational studies involving small peptides, it is useful to apply Le Chatelier's Principle to the equilibrium below:
random coil \(\rightleftharpoons \) helix
Anything perturbant (small molecules, solvent, etc) that would preferentially interact with the helical form would push the equilibrium to the helical form.
Early models assumed that intrachain H bonds were energetically (enthalpically) more favorable than H bonds between peptide and water. But to form a hydrogen bond requires an entropy payback since a helix is much more ordered (lower entropy) than a random coil (higher entropy). At low temperature, enthalpy predominates and helix formation in solution is favored. At high temperature, the helix is disfavored entropically. Imagine the increased vibrational and rotational states permitted to the atoms at higher temperatures. (Remember the trans to gauche conformational changes in the acyl chains of double chain amphiphiles as the temperature increased, leading to a transition from a gel to liquid crystalline phase in bilayer vesicles.) Theoretical studies on helix-coil transitions predict the following:
- as the chain length increases, the helix gets more stable;
- increasing the charge on the molecule destabilizes the helix, since the coil, compared to the more compact helix, has a lower charge density;
- solvents that protonate the carbonyl oxygen (like formic acid) destabilizes the helix; and
- solvents that form strong H bonds compete with the peptide and destabilize the helix. In contrast, solvents such as CHCl3 and dimethylformamide (a nonprotic solvent), stabilize the helix. Likewise 2-chloroethanol and trifluoroethanol, which form none or weaker H bonds to the peptide than does water, stabilizes the helix. (In the case of trifluoroethanol, molecular dynamics simulations have shown that TFE preferentially inteacts with (solvates) the peptide, which inhibits H bonds from the peptide backbone to water, stabilizing the intrahelical H bonds.
These helix-coil studies suggest that H bonds are important in stabilizing a protein.
But do they really? Why should these H bonds differ from those in water? It's difficult to figure out whether they are since there are so many possible H bonds (between protein and water, water and water, and protein and protein), and their strength depends on their orientation and the dielectric constant of the medium in which they are located.
If intrachain H bonds in a protein are not that much different in energy than intermolecular H bonds between the protein and water, and given that proteins are marginally stable at physiological temperatures, then it follows that the folded state must contain about as many intramolecular hydrogen bonds within the protein as possible intermolecular H bonds between the protein and water, otherwise the protein would unfold.
To resolve this issue, and determine the relative strength of H bonds between the varying possible donors and acceptors, many studies have been conducted to compare the energy of H bonds between small molecules in water with the energy of H bonds between the same small molecules but in a nonpolar solvent. The rationale goes like this. If the interior of a protein is more nonpolar than water (lower dielectric constant than water), then intrastrand H bonds in a protein might be modeled by looking at the H bonds between small molecules in nonpolar solvents and asking the question, is the free energy change for the following process < 0:
Dw + Aw \(\rightleftharpoons \) (DA)n, DGo, K
where D is a hydrogen bond donor (like NH) and A is a hydrogen bond acceptor, (like C=O), w is water (i.e. donor and acceptor are in water), and n is a nonpolar solvent, and DGo and K are the standard free energy change and the equilibrium constant, respectively, for the formation of a H-bond in a nonpolar solvent from a donor and acceptor in water. This reaction simulates H-bond contributions to protein folding, where a buried H-bond is mimicked by a H-bond in a nonpolar solvent. The reaction written above is really a thought experiment, since it would be hard to set up the necessary conditions to make the measurement. However, we can calculate the DGo for this reaction since it is a state function and it really doesn't matter how one accomplishes this process.
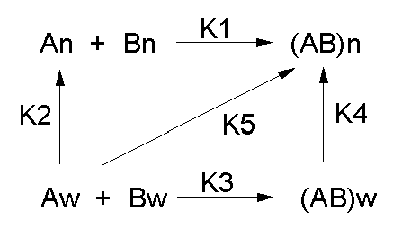
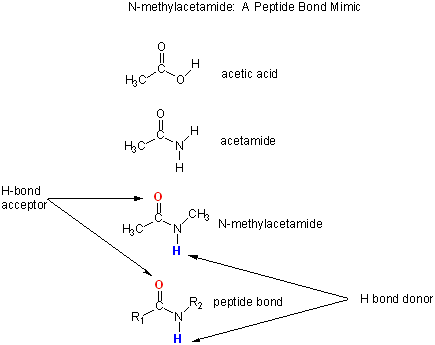
Let's consider a specific example: the formation of H bonds between two molecules of N-methylacetamide (NMA) in water and in a nonpolar solvent. The reaction scheme shown below describes a set of reactions (a thermodynamic cycle) involving the formation of H-bonded dimers of NMA . A and B are both molecules of NMA, in either water (w) or a nonpolar solvent (n).
N-methylacetamide is a good mimic for the H bond donors and acceptors of the peptide bond of a polypeptide chain.
In the reaction scheme shown above,
K1 is the equilibrium constant for the dimerization of NMA in a nonpolar medium. This can be readily determined, and is >1, implying that DGo < 0. (Remember, DGo = -RTlnKeq) For the dimerization of NMA in CCl4, DGo1 = -2.4 kcal/mol.
K2 is the equilibrium constant (think of it as a partition coefficient) for the transfer of two NMA molecules from water to a nonpolar solvent (again easily measurable). For NMA transferring from water to CCl4, DGo2 = + 6.12 kcal/mol.
K3 is the equilibrium constant for the dimerization of NMA in water. This can be readily determined, and is <1, implying that DGo > 0. For the dimerization of NMA in water, DGo3 = +3.1 kcal/mol.
K4 is the equilibrium constant (think of it as a partition coefficient) for the transfer of a hydrogen-bonded dimer of NMA from water to a nonpolar solvent. You try to think of a way to measure that! I can't. This is where thermodynamic cycles comes in so nicely. You don't have to measure it. You can calculate it from K1-3 since DGo is a state function!
\[ \Delta G^o_2 + \Delta G^o_1 = \Delta G^o_3 + \Delta G^o_4 \hspace{15px}\textrm{ or }\hspace{15px} -RT\ln K_2 + -RT\ln K_1 = -RT\ln K_3 + -RT\ln K_4 \]
\[ \ln K_2 + \ln K_1 = \ln K_3 + \ln K_4 = \ln(K_2K_1 )= \ln(K_3K_4) \hspace{15px}\textrm{ or }\hspace{15px} (K_2K_1 )= (K_3K_4) \]
For NMA transferring from water to CCl4, D Go4 = + 0.62 kcal/mol.
(Note: Biochemists like to talk about thermodynamic cycles which may seem new to you. However, believe it or not, you have seen them before - in General Chemistry - in the form of Hess's Law!)
From K1-4and the corresponding DGo values, we can now calculate DGo5 for the formation of H-bonded NMA dimers in a nonpolar solvent from two molecules of NMA(aq). This reaction, which we hope simulates formation of buried intrachain H bonds in proteins on protein folding, is:,
Dw + Aw \(\rightleftharpoons\) (DA)n, for which DGo5= +3.72 (i.e. disfavored).
If this model is a good mimic for studying H bond formation on protein folding, it suggests that the formation of buried H bonds during protein folding does not drive protein folding.
However, if the transfer of D and A (from a large protein) from water to the nonpolar medium (modeled by K2) is driven by other forces (such as the hydrophobic effect), the positive value of K1 will strongly favored buried H bond formation. So, if this happens in proteins, it is clear why so many intrachain H bonds occur, since K1 is so favored. H bonds may not assist the collapse of a protein, but would favor internal organization within a compact protein. That is, H bonds don't drive protein folding per se, but form so that the folded protein would not be destabilized by too many unsatisfied H bonds.
There are potential problems with this simple model. The interior of a protein is not homogeneous (i.e. the effective dielectric within the protein will vary). H bond strength is also very sensitive to geometry. Also, there are many H bonds within a protein, so slight errors in the estimation of H bond strength would lead to large errors in determination of protein stability.
Another argument against H bonds being the determining factor in protein folding and stability comes from solvent denaturation studies. If intrachain H bonds are so important, then should not solvents that can H bond to the backbone denature the protein? Shouldn't water (55 M) act as a denaturant? It doesn't, however. Dioxane (5 member heterocyclic ring with O) which has only a H bond acceptor wouldn't be expected to denature proteins, but it does. H bonds also increase in nonpolar solvents. Peptides which have random structures in water can be induced to form helices when placed in alcohol solutions (trifluorethanol, for example), which are more nonpolar than water, as explained above in the helix-coil studies. If H bonds are the dominate factor in protein stability, the alcohols would stabilize proteins. At low concentrations of alcohol, proteins are destabilized.
Hence, based on small molecule studies and the study of protein in various cosolvents, it is unlikely that H bonds are the big stabilizers of protein structure. Only 11% of all C=O's and 12% of all NH's in protein have no H bonds (determined by analysis of X ray crystallographic structures). Of all H bonds to C=O, 43% are to water, 11% to side chains, and 46% to main chain NH's. Of all H bonds to NH, 21% are to water, 11% to side chains, and 68% to the main chain C=O. We will see later, however, than an opposite conclusion is reached from studies using site-specific mutagenesis.


