Chemical Equilibrium—Part 1: Forward and Reverse Reactions
- Page ID
- 9361
Chemical equilibrium—Part 1: forward and reverse reactions
Understanding the concept of chemical equilibrium is critical to following several of the discussions that we have in BIS2A and indeed throughout biology and the sciences. It is difficult to completely describe the concept of chemical equilibrium without reference to the energy of a system, but for the sake of simplicity, let’s try anyway and reserve the discussion of energy for another chapter. Let us, rather, begin developing our understanding of equilibrium by considering the reversible reaction below:

Hypothetical reaction #1: A hypothetical reaction involving compounds A, B and D. If we read this from left to right, we would say that A and B come together to form a larger compound: D. Reading the reaction from right to left, we would say that compound D breaks down into smaller compounds: A and B.
We first need to define what is meant by a “reversible reaction.” The term “reversible” simply means that a reaction can proceed in both directions. That is, the things on the left side of the reaction equation can react together to become the things on the right of the equation, AND the things on the right of the equation can also react together to become the things on the left side of the equation. Reactions that only proceed in one direction are called irreversible reactions.
To start our discussion of equilibrium, we begin by considering a reaction that we posit is readily reversible. In this case, it is the reaction depicted above: the imaginary formation of compound D from compounds A and B. Since it is a reversible reaction, we could also call it the decomposition of D into A and B. Let us, however, imagine an experiment in which we watch the reaction proceed from a starting point where only A and B are present.
Example #1: Left-balanced reaction
| Concentration | t=0 | t=1 | t=5 | t=10 | t=15 | t=20 | t=25 | t=30 | t=35 | t=40 |
|---|---|---|---|---|---|---|---|---|---|---|
| [A] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [B] | 100 | 90 | 80 | 70 | 65 | 62 | 60 | 60 | 60 | 60 |
| [C] | 0 | 10 | 20 | 30 | 45 | 38 | 40 | 40 | 40 | 40 |
At time t = 0 (before the reaction starts), the reaction has 100 concentration units of compounds A and B and zero units of compound D. We now allow the reaction to proceed and observe the individual concentrations of the three compounds over time (t=1, 5, 10, 15, 20, 25, 30, 35, and 40 time units). As A and B react, D forms. In fact, one can see D forming from t=0 all the way to t=25. After that time, however, the concentrations of A, B and D stop changing. Once the reaction reaches the point where the concentrations of the components stop changing, we say that the reaction has reached equilibrium. Notice that the concentrations of A, B, and D are not equal at equilibrium. In fact, the reaction seems left balanced so that there is more A and B than D.
Note
****Common student misconception warning****
Many students fall victim to the misconception that the concentrations of a reaction’s reactants and products must be equal at equilibrium. Given that the term equilibrium sounds a lot like the word “equal,” this is not surprising. But as the experiment above tries to illustrate, this is NOT correct!
Example #2: right-balanced reaction
We can examine a second hypothetical reaction, the synthesis of compound J from the compounds E and F.

Hypothetical reaction #2: A hypothetical reaction involving compounds E, F and J. If we read this from left to right, we would say that E and F come together to form a larger compound: J. Reading the reaction from right to left, we would say that compound J breaks down into smaller compounds: E and F.
The structure of hypothetical reaction #2 looks identical to that of hypothetical reaction #1, which we considered above—two things come together to make one bigger thing. We just need to assume, in this case, that E, F, and J have different properties from A, B, and D. Let’s imagine a similar experiment to the one described above and examine this data:
Hypothetical reaction #2: time course
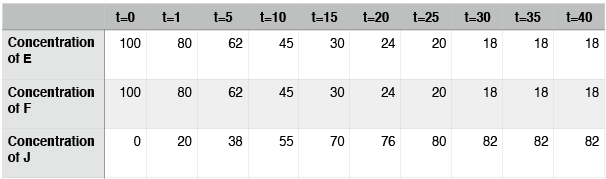
In this case, the reaction also reaches equilibrium. This time, however, equilibrium occurs at around t=30. After that point, the concentrations of E, F, and J do not change. Note again that the concentrations of E, F, and J are not equal at equilibrium. In contrast to hypothetical reaction #1 (the ABD reaction), this time the concentration of J, the thing on the right side of the arrows, is at a higher concentration than E and F. We say that, for this reaction, equilibrium lies to the right.
Four more points need to be made at this juncture.
Point 1: Whether equilibrium for a reaction lies to the left or the right will be a function of the properties of the components of the reaction and the environmental conditions that the reaction is taking place in (e.g., temperature, pressure, etc.).
Point 2: We can also talk about equilibrium using concepts of energy, and we will do this soon, just not yet.
Point 3: While hypothetical reactions #1 and #2 appear to reach a point where the reaction has “stopped,” you should imagine that reactions are still happening even after equilibrium has been reached. At equilibrium the “forward” and “reverse” reactions are just happening at the same rate. That is, in example #2, at equilibrium J is forming from E and F at the same rate that it is breaking down into E and F. This explains how the concentrations of the compounds aren’t changing despite the fact that the reactions are still happening.
Point 4: From this description of equilibrium, we can define something we call the equilibrium constant. Typically, the constant is represented by an uppercase K and may be written as Keq. In terms of concentrations, Keq is written as the mathematical product of the reaction product concentrations (stuff on the right) divided by the mathematical product of the reactant concentrations (stuff on the left). For example, Keq,1 = [D]/[A][B], and Keq,2 = [J]/[E][F]. The square brackets "[]" indicate the “concentration of” whatever is inside the bracket.

