Solutions for Apr. 22, 2008, First Midterm
- Page ID
- 6777
\[\mathbf{BioSci\: 102-02\\ Apr. 22,\: 2008,\: First\: Midterm}\]
Instructions:
• There are seven pages in this exam including the cover sheet, please count them before you start to make sure all are present.
• Write your name on each page of the exam.
• Write your answers in the space provided below each question. If you need more space use the back of the page and indicate clearly that you have continued your answer on the back. Do not use additional paper. For calculation problems a clear line of calculations leading to your final answer must be shown to obtain full credit.
Use the following \(\mathrm{pK_{a}}\) values for the exam.
| Amino Acid | \(\mathbf{\alpha -NH_{2}}\) | \(\mathbf{\alpha -COOH}\) | R-group |
|---|---|---|---|
| Ala, Gly, Ile, Leu, Val | 9.7 | 2.3 | \(-\) |
| Asn, Gln | 9.0 | 2.1 | \(-\) |
| Met, Ser, Trp | 9.3 | 2.3 | \(-\) |
| Phe | 9.1 | 1.8 | \(-\) |
| Pro | 10.6 | 2.0 | \(-\) |
| Thr | 10.4 | 2.6 | \(-\) |
| Asp | 9.8 | 2.1 | 3.9 |
| Glu | 9.7 | 2.2 | 4.2 |
| His | 9.2 | 1.8 | 6.0 |
| Cys | 10.8 | 1.8 | 8.3 |
| Tyr, Lys | 9.1 | 2.2 | 10.0 |
| Arg | 9.0 | 2.2 | 12.5 |
\(\begin{matrix} \mathrm{log\: 1.0=0.00}\\ \mathrm{log\: 1.5=0.18} \\ \mathrm{log\: 2.0=0.18}\\ \mathrm{log\: 2.5=0.40}\\ \mathrm{log\: 3.0=0.48}\\ \mathrm{log\: 3.5=0.54}\\ \mathrm{log\: 4.0=0.60}\\ \mathrm{log\: 4.5=0.65}\\ \mathrm{log\: 5.0=0.70}\\ \mathrm{log\: 5.5=0.74}\\ \mathrm{log\: 6.0=0.78}\\ \mathrm{log\: 6.5= 0.81}\\ \mathrm{log\: 7.0=0.85}\\ \mathrm{log\: 7.5=0.88}\\ \mathrm{log\: 8.0=0.90}\\ \mathrm{log\: 8.5=0.93}\\ \mathrm{log\: 9.0=0.95}\\ \mathrm{log\: 9.5=0.98}\\ \mathrm{log\: 10.0=1.00} \end{matrix}\)
\(\mathbf{R=8.3\times 10^{-3}\: kJ/ ^{\circ}K\cdot mol}\)
\(\mathbf{25^{\circ}C=298K}\)
| Question | Value | Score |
|---|---|---|
| 1 | 18 | |
| 2 | 12 | |
| 3 | 12 | |
| 4 | 12 | |
| 5 | 16 | |
| 6 | 20 | |
| 7 | 14 | |
| 8 | 16 | |
| 9 | 10 | |
| 10 | 20 | |
| Total | 150 |
1. (18) In each blank, write the name of the strongest of the weak interactions that would be likely to occur between the side chains of the two amino acids listed next to the blank (assume an aqueous solution at pH7).
Hydrophobic interaction F and W
H-bond Gln and Asn
Hydrophobic interaction Methionine and Leucine
Salt Bridge K and D
H-bond Ser and Ser
H-bond D and N
2. Some biochemical applications require concentrated solutions of cesium chloride (CsCl). To make up such a solution you add 2 g of solid CsCl to 10 ml of room temperature (\(\mathrm{25^{\circ}C}\)) water and begin to mix it. As the CsCl dissolves you feel the mixture getting noticeably cold to the touch. When the CsCl is completely dissolved you measure the temperature of the solution and find it to be \(\mathrm{4^{\circ}C}\).
a) (4) Is \(\Delta \mathrm{G}\) for the dissolution of CsCl in water at room temperature \(\mathrm{\fbox{less than}}\), greater than, or equal to zero? (circle correct answer). Why?
The reaction was spontaneous at constant pressure so it must have a negative \(\mathbf{ \Delta G}\).
b) (4) Is \(\mathrm{ \Delta H}\) for the dissolution of CsCl in water at room temperature less than, \(\mathrm{\fbox{greater than}}\), or equal to zero? (circle correct answer) Why? The temperature of the solution decreased because heat was taken up by the reaction. This is defined as a positive enthalpic change.
c) (4) Is \(\mathrm{\Delta S}\) for the dissolution of CsCl in water at room temperature less than, \(\mathrm{\fbox{greater than}}\), or equal to zero? (circle correct answer) Why?
\(\mathbf{\Delta G=\Delta H -T\Delta S}\). Since \(\mathbf{\Delta G}\) is less than zero and \(\mathbf{\Delta H}\) is positive, \(\mathbf{\Delta S}\) must be positive for the equation to balance.
3. (12) Consider the following set of reactions and \(\mathrm{\Delta G^{\circ’}}\) values.
\[\begin{matrix} \mathrm{A+B \Leftrightarrow C} & \mathrm{\Delta G^{\circ’}=-1.7\: KJ/mol} \\ \mathrm{C \Leftrightarrow D} & \mathrm{\Delta G^{\circ’}=0.1\: KJ/mol}\\ \mathrm{E \Leftrightarrow D} & \mathrm{\Delta G^{\circ’}=4.2\: KJ/mol} \end{matrix}\]
What is the \(\mathrm{\Delta G^{\circ’}}\) for the reaction \(\mathrm{A+B \Leftrightarrow E}\)?
\[\begin{matrix} \mathrm{A+B \Leftrightarrow C} & \mathrm{\Delta G ^{\circ’}=-1.7\: KJ/mol} & \: \\ \mathrm{C \Leftrightarrow D} & \mathrm{\Delta G^{\circ’} = 0.1\: KJ/mol} & \: \\ \mathrm{D \Leftrightarrow E} & \mathrm{\Delta G^{\circ’}=-4.2\: KJ/mol} & \mathbf{(reverse\: reaction,\: change\: sign)} \\ \hline \mathrm{A+B \Leftrightarrow E} & \mathrm{\Delta G^{\circ’}=-5.8\: KJ/mol} & \: \end{matrix}\]
\(\mathrm{\Delta G^{\circ’}} = \underline{\mathbf{-5.8\: kJ/mol}}\) units
4. (12) Tris is a weak base with a \(\mathrm{pK_{a}}\) of 8.1. You have in the lab 1.0 M solutions of each of Tris base, HCl and NaOH. What volume of each of these solutions would you use to prepare 1.0 liters of 0.1 M Tris buffer at pH 8.4? (note: you may not need to use all three, and assume that you can add water to get the correct volume)
Must add 0.1 liters (100 ml) of Tris base to provide the necessary 0.1 moles of total Tris
\(\mathbf{8.4=8.1+log[Tris]/[TrisHCl]}\)
\(\mathbf{0.3=log[Tris]/[TrisHCl]}\)
\(\mathbf{[Tris]/[TrisHCl]=2;\: [Tris]=2[TrisHCl]}\)
\(\mathbf{[Tris]+[TrisHCl]=0.1\: M}\)
\(\mathbf{2[TrisHCl]+[TrisHCl]=0.1\: M}\)
\(\mathbf{3[TrisHCl]=0.1\: M}\)
\(\mathbf{[TrisHCl]=0.033\: M}\)
\(\mathbf{[Tris]=0.067\: M}\)
Must add 0.033 liters (33 ml) of 1 M HCl to convert 0.033 moles of Tris to TrisHCl
Then add water to make 1.0 liters total.
\(\begin{matrix} \mathrm{NaOH}\: \underline{ \mathbf{0}} & \mathrm{HCl}\: \underline{ \mathbf{33\: ml}} & \mathrm{Tris}\: \underline{\mathbf{100\: ml}} \end{matrix}\)
5. (16) Place an X next to the ONE correct answer to each of the following questions.
a) A hydrogen bond can act between?
A hydrogen in a hydrocarbon and a nitrogen in an amine.
An amide nitrogen and a carbonyl oxygen.
A hydrogen on an amide nitrogen and a hydrogen on an oxygen in a carboxylic acid group.
X A carboxyl oxygen and a hydrogen on an oxygen in a hydroxyl group.
A hydroxyl hydrogen and a carboxyl carbon.
b) The pH of a buffered solution is determined by:
The total concentration and the \(\mathrm{pK_{a}}\) of the buffer.
The \(\mathrm{pK_{a}}\) of the buffer and the concentration of the acid form.
X The \(\mathrm{\Delta G^{\circ’}}\) of dissociation of the acid form of the buffer and the mole ration of the acid and base forms.
The \(\mathrm{pK_{a}}\) of the buffer and the concentration of the base form.
The total concentration and the \(\mathrm{pK_{b}}\) of the buffer.
c). Edman’s reagent (phenylisothiocyanate, PITC) is:
Used to cleave disulfide bonds.
Able to remove the C-terminal amino acids from proteins.
Equivalent in function to Sanger’s reagent (fluorodinitrobenzyne, FDNB).
Used to cleave proteins into large fragments.
X Able to attach to the N-terminus of a protein, and also to remove the first amino acid from a protein.
d) A conjugate base:
X Will have a charge that is one less than the charge of its conjugate acid.
Will quantitatively remove a proton from its conjugate acid.
Will have a charge ≤ 0.
Is an \(\mathrm{OH^{-}}\) acceptor.
Has a lower Gibbs free energy than its conjugate acid.
6. The following peptides were obtained by partial hydrolysis of a purified protein. Answer the questions below by writing the number(s) corresponding to the peptides in the spaces below. (give all correct answers if more than one peptide answers the question).
1. ThrMetValAsnLys
2. PDECE
3. FEEHG
4. MetTrpArgLysLys
5. QTSPA
6. NQIGF
7. IAFVL
a) (4) Which peptide(s) could be readily cleaved by chymotrypsin.
3, 4, 7 (F, W, or Y in any but the last position)
b) (4) Which peptide(s) contain sulfur?
1, 2, 4, (contains Cis (C) or Met (M))
c) (4) Which peptide could bind most strongly to peptide #4 by salt bridges?
2 (2 is most negative (D and E) to pair with the strong positive charge of 4)
d) (4) Which is the most hydrophobic peptide?
7 (no charged or polar AA)
e) (4) Which peptide(s) could be cleaved by cyanogen bromide?
1, 4 (Met, M, at any but the last position)
7. (14) The compound TES is a weak acid with a \(\mathrm{pK_{a}}\) of 7.5 that is often used as a buffer in biochemistry. A biochemical reaction is buffered with TES at pH 7.5. After 10 min, the reaction has produced \(\mathrm{0.004\: M\: H^{+}}\) and the pH has changed to 7.2. What was the original total buffer concentration in the solution?
Start : \(\mathbf{pH=pK_{a}}\) so [TES-](base form) = [TES] = 0.5 x, where x = total buffer concentration.
End: [TES-] = 0.5 x - 0.004; [TES] = 0.5 x + 0.004
\[\mathrm{pH=pK_{a}+log \dfrac{0.5x-0.004}{0.5x+0.004}}\]
\[\mathrm{7.2=7.5+log \dfrac{0.5x-0.004}{0.5x+0.004}}\]
\[\mathrm{log \dfrac{0.5x-0.004}{0.5x+0.004}=-0.3}\]
\[\mathrm{\dfrac{0.5x-0.004}{0.5x+0.004}=0.5}\]
\[\mathrm{0.5x-0.004=-.5(0.5x+0.004)=0.25x+0.002}\]
\[\mathrm{0.25x=0.006}\]
\[\mathrm{x=0.024}\]
Buffer concentration = 0.024 M units
8. (16) The following solutions of amino acids were passed through an ion exchange column containing sulfonated polystyrene resin. For each solution, circle "B" if the amino acid will bind tightly to the column, and "F" if the amino acid will flow through the column, under the conditions given.
B \(\mathrm{\fbox{F}}\) Amino acid D at pH 7 (\(\mathrm{\alpha -N =+1,\: \alpha -C=-1,\: R=-1,\: total=-1}\))
\(\mathrm{\fbox{B}}\) F Lys at pH 9.1 (\mathrm{\alpha -N=+0.5,\: \alpha -C=-1,\: R~+0.8,\: total~+0.3}\))
\(\mathrm{\fbox{B}}\) F Amino acid R at pH 8 (\(\mathrm{\alpha -N=+1,\: \alpha -C=-1,\: R=+1,\: total=+1}\))
B \(\mathrm{\fbox{F}}\) Amino acid Y at pH 9.1 (\(\mathrm{\alpha -N=+0.5,\: \alpha -C=-1,\: R~-0.1,\: total~-0.6}\))
9. (10) The phosphorylation of glucose (Glc) is a critical reaction in energy metabolism in essentially all organisms. It occurs according to the following reaction:
\[\mathrm{Glc+ATP \Leftrightarrow G-6-P + ADP \: K'_{eq}=856\: @\: 25^{\circ}C}\]
Given the following concentrations in a cell: [G-6-P] = 10 mM, [ADP] = 10 mM, [ATP] = 0.1 mM, what would the equilibrium concentration of Glucose (Glc) be under these conditions?
\[\mathrm{K_{eq}=\dfrac{[G6P][ADP]}{[Glc][ATP]}}\]
\[\mathrm{856=\dfrac{10\times 10^{-3}M \cdot 10\times 10^{-3}M}{[Glc]\cdot 0.1\times 10^{-3}M}}\]
\[\mathrm{856=\dfrac{10^{-4}M^{2}}{[Glc]\cdot 10^{-4}M}=\dfrac{1}{[Glc]}}\]
\[\mathrm{[Glc]=\dfrac{1}{856}=1.17\times 10^{-3}M\: or\: 1.17\: mM}\]
[Glc] = \(\mathrm{1.17\times 10^{-3}\: M}\) units
10. a) (10) Draw the complete chemical structure of the dipeptide CysMet in the ionic form that would predominate at pH 8.6.
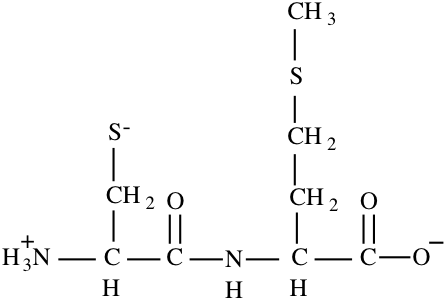
b) (10) To the nearest 0.1 charge unit, what is the net charge on this dipeptide at pH 8.6?
N-term – pKa = 10.8 Charge = +1
C-term – pKa = 2.3 Charge = -1
For side chain sulfhydryl:
\(\mathrm{8.6 = 8.3 + log [S^{-}]/[SH]; [S^{-}]/[SH] = 2; [S^{-}] = 2[SH]
[S^{-}] + [SH] = 1; 2[SH] + [SH] = 1; 3[SH] = 1; [SH] = 0.33 so [S^{-}] = 0.67, charge = -0.67}\)
Total Charge = +1 -1 -0.67 = -0.67
Charge = -0.67

