12.3D: Mendel’s Law of Independent Assortment
- Page ID
- 13272
- Use the probability or forked line method to calculate the chance of any particular genotype arising from a genetic cross
Independent Assortment
Mendel’s law of independent assortment states that genes do not influence each other with regard to the sorting of alleles into gametes: every possible combination of alleles for every gene is equally likely to occur. The independent assortment of genes can be illustrated by the dihybrid cross: a cross between two true-breeding parents that express different traits for two characteristics. Consider the characteristics of seed color and seed texture for two pea plants: one that has green, wrinkled seeds (yyrr) and another that has yellow, round seeds (YYRR). Because each parent is homozygous, the law of segregation indicates that the gametes for the green/wrinkled plant all are yr, while the gametes for the yellow/round plant are all YR. Therefore, the F1 generation of offspring all are YyRr.
For the F2 generation, the law of segregation requires that each gamete receive either an R allele or an r allele along with either a Y allele or a y allele. The law of independent assortment states that a gamete into which an r allele sorted would be equally likely to contain either a Y allele or a y allele. Thus, there are four equally likely gametes that can be formed when the YyRr heterozygote is self-crossed as follows: YR, Yr, yR, and yr. Arranging these gametes along the top and left of a 4 × 4 Punnett square gives us 16 equally likely genotypic combinations. From these genotypes, we infer a phenotypic ratio of 9 round/yellow:3 round/green:3 wrinkled/yellow:1 wrinkled/green. These are the offspring ratios we would expect, assuming we performed the crosses with a large enough sample size.
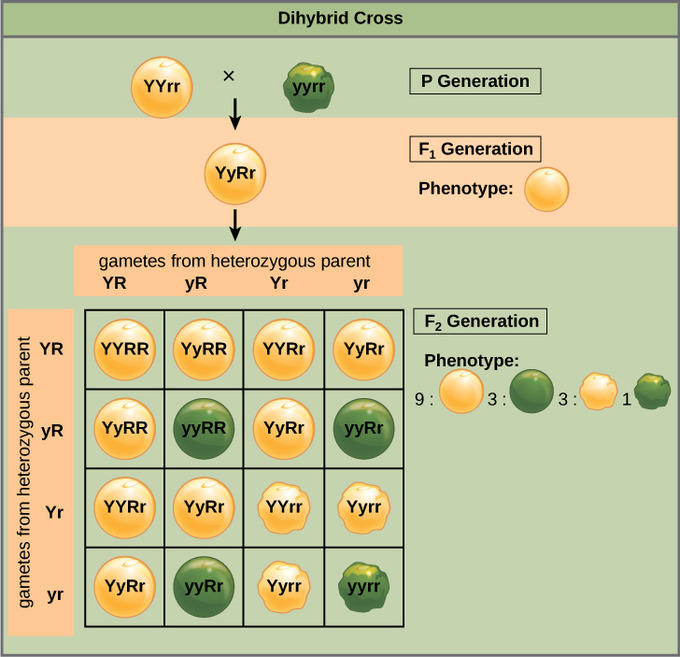
Because of independent assortment and dominance, the 9:3:3:1 dihybrid phenotypic ratio can be collapsed into two 3:1 ratios, characteristic of any monohybrid cross that follows a dominant and recessive pattern. Ignoring seed color and considering only seed texture in the above dihybrid cross, we would expect that three-quarters of the F2 generation offspring would be round and one-quarter would be wrinkled. Similarly, isolating only seed color, we would assume that three-quarters of the F2offspring would be yellow and one-quarter would be green. The sorting of alleles for texture and color are independent events, so we can apply the product rule. Therefore, the proportion of round and yellow F2 offspring is expected to be (3/4) × (3/4) = 9/16, and the proportion of wrinkled and green offspring is expected to be (1/4) × (1/4) = 1/16. These proportions are identical to those obtained using a Punnett square. Round/green and wrinkled/yellow offspring can also be calculated using the product rule as each of these genotypes includes one dominant and one recessive phenotype. Therefore, the proportion of each is calculated as (3/4) × (1/4) = 3/16.
Forked-Line Method
When more than two genes are being considered, the Punnett-square method becomes unwieldy. For instance, examining a cross involving four genes would require a 16 × 16 grid containing 256 boxes. It would be extremely cumbersome to manually enter each genotype. For more complex crosses, the forked-line and probability methods are preferred.
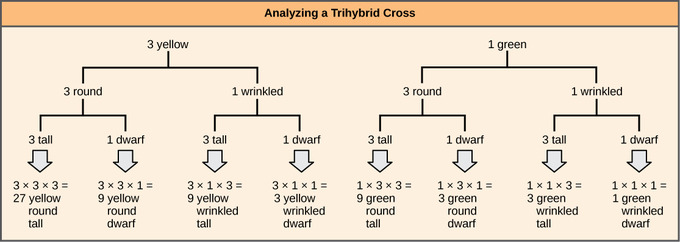
To prepare a forked-line diagram for a cross between F1 heterozygotes resulting from a cross between AABBCC and aabbcc parents, we first create rows equal to the number of genes being considered and then segregate the alleles in each row on forked lines according to the probabilities for individual monohybrid crosses. We then multiply the values along each forked path to obtain the F2 offspring probabilities. Note that this process is a diagrammatic version of the product rule. The values along each forked pathway can be multiplied because each gene assorts independently. For a trihybrid cross, the F2phenotypic ratio is 27:9:9:9:3:3:3:1.
Probability Method
While the forked-line method is a diagrammatic approach to keeping track of probabilities in a cross, the probability method gives the proportions of offspring expected to exhibit each phenotype (or genotype) without the added visual assistance.
To fully demonstrate the power of the probability method, however, we can consider specific genetic calculations. For instance, for a tetrahybrid cross between individuals that are heterozygotes for all four genes, and in which all four genes are sorting independently in a dominant and recessive pattern, what proportion of the offspring will be expected to be homozygous recessive for all four alleles? Rather than writing out every possible genotype, we can use the probability method. We know that for each gene the fraction of homozygous recessive offspring will be 1/4. Therefore, multiplying this fraction for each of the four genes, (1/4) × (1/4) × (1/4) × (1/4), we determine that 1/256 of the offspring will be quadruply homozygous recessive.
Key Points
- Mendel’s law of independent assortment states that genes do not influence each other with regard to the sorting of alleles into gametes; every possible combination of alleles for every gene is equally likely to occur.
- The calculation of any particular genotypic combination of more than one gene is, therefore, the probability of the desired genotype at the first locus multiplied by the probability of the desired genotype at the other loci.
- The forked line method can be used to calculate the chances of all possible genotypic combinations from a cross, while the probability method can be used to calculate the chance of any one particular genotype that might result from that cross.
Key Terms
- independent assortment: separate genes for separate traits are passed independently of one another from parents to offspring


