13.4: ML and Bayesian Tests for State-Dependent Diversification
- Page ID
- 21659
Now that we can calculate the likelihood for state-dependent diversification models, formulating ML and Bayesian tests follows the same pattern we have encountered before. For ML, some comparisons are nested and so you can use likelihood ratio tests. For example, we can compare the full BiSSe model (Maddison et al. 2007), with parameters q01, q10, λ0, λ1, μ0, μ1 with a restricted model with parameters q01, q10, λall, μall. Since the restricted model is a special case of the full model where λ0 = λ1 = λall and μ0 = μ1 = μall, we can compare the two using a likelihood ratio test, as described earlier in the book. Alternatively, we can compare a series of BiSSe-type models by comparing their AICc scores.
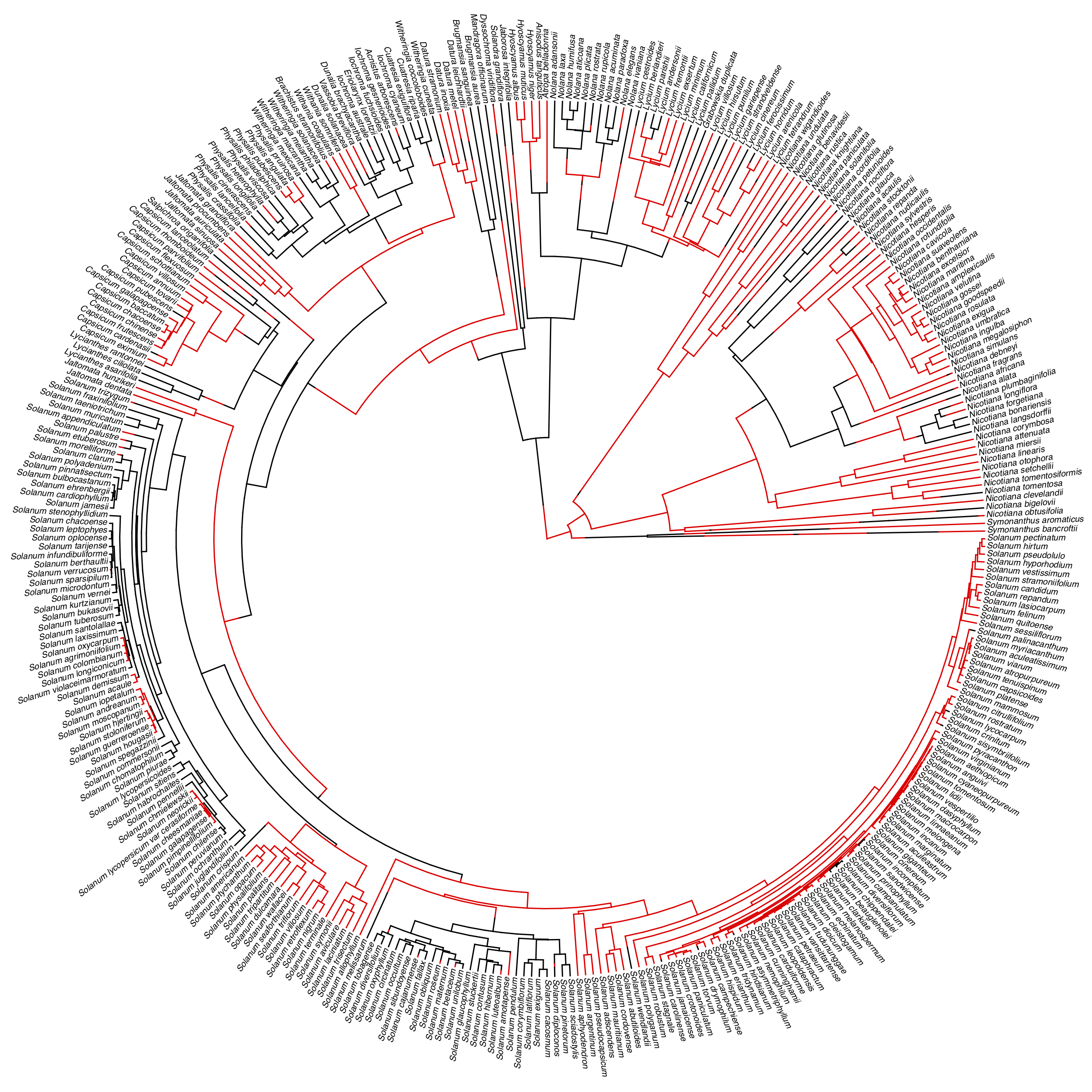
For example, I will apply this approach to the example of self-incompitability. I will use data from Goldberg and Igic (2012), who provide a phylogenetic tree and data for 356 species of Solanaceae. All species were classified as having any form of self incompatibility, even if the state is variable among populations. The data, along with a stochastic character map of state changes, are shown in Figure 13.4. Applying the BiSSe models to these data and assuming that q01 ≠ q10, we obtain the following results:
| Model | Number of parameters | Parameter estimates | lnL | AIC |
|---|---|---|---|---|
| Character-independent model | 4 | λ = 0.65, μ = 0.57 | -945.96 | 1899.9 |
| q01 = 0.16, q10 = 0.09 | ||||
| Speciation rate depends on character | 5 | μ = 0.57 | -945.57 | 1901.1 |
| λ0 = 0.69, λ1 = 0.63 | ||||
| q01 = 0.17, q10 = 0.08 | ||||
| Extinction rate depends on character | 5 | λ = 0.65 | -943.93 | 1897.9 |
| μ0 = 0.45, μ1 = 0.67 | ||||
| q01 = 0.22, q10 = 0.06 | ||||
| Full character-dependent model | 6 | λ0 = 0.49, λ1 = 0.79 | -941.94 | 1895.9 |
| μ0 = 0.20, μ1 = 0.84 | ||||
| q01 = 0.29, q10 = 0.05 |
From this, we conclude that models where the character influences diversification fit best, with the full model receiving the most support. We can't discount the possibility that the character only influences extinction and not speciation, since that model is within 2 AIC units of the best model.
Alternatively, we can carry out a Bayesian test for state-dependent diversification.
Bayesian test for state-dependent diversification
Like other models in the book, this requires setting up an MCMC algorithm that samples the posterior distributions of our model parameters (FitzJohn 2012). In this case:
- Sample a set of starting parameter values, q01, q10, λ0, λ1, μ0, μ1, from their prior distributions. For example, one could set prior distribution for all parameters as exponential with a mean and variance of λpriori (note that, as usual, the choice for this parameter should depend on the units of tree branch lengths you are using). We then select starting values for all parameters from the prior.
- Given the current parameter values, select new proposed parameter values using the proposal density Q(p′|p). For all parameter values, we can use a uniform proposal density with width wp, so that Q(p′|p) U(p − wp/2, p + wp/2). We can either choose all parameter values simultaneously, or one at a time (the latter is typically more effective).
- Calculate three ratios:
- The prior odds ratio. This is the ratio of the probability of drawing the parameter values p and p′ from the prior. Since we have exponential priors for all parameters, we can calculate this ratio as: \[ R_{prior} = \frac{\lambda_{prior_i} e^{-\lambda_{prior_i} p'}}{\lambda_{prior_i} e^{-\lambda_{prior_i} p}}=e^{\lambda_{prior_i} (p-p')} \label{13.11}\[
- The proposal density ratio. This is the ratio of probability of proposals going from p to p′ and the reverse. We have already declared a symmetrical proposal density, so that Q(p′|p)=Q(p|p′) and Rproposal = 1.
- The likelihood ratio. This is the ratio of probabilities of the data given the two different parameter values. We can calculate these probabilities from the approach described in the previous section.
- Find Raccept as the product of the prior odds, proposal density ratio, and the likelihood ratio. In this case, the proposal density ratio is 1, so (eq. 13.12):
Raccept = Rprior ⋅ Rlikelihood


