7.5: Simulating the Mk model on a tree
- Page ID
- 21617
We can also use the equations above to simulate evolution under an Mk or extended-Mk model on a tree (Felsenstein 2004). To do this, we simulate character evolution on each branch of the tree, starting at the root and progressing towards the tips. At speciation, we assume that both daughter species inherit the character state of their parental species immediately following speciation, and then evolve independently after that. At the end of the simulation, we will obtain a set of character states, one for each tip in the tree. The distribution of character states will depend on the shape of the phylogenetic tree (both its topology and branch lengths) along with the parameters of our model of character evolution.
We first draw a beginning character state at the root of the tree. There are several common ways to do this. For example, we can either draw from the stationary distribution or from one where each character state is equally likely. In the case of the standard Mk model, these are the same. For example, if we are simulating evolution under Mk with k = 2, then state 0 and 1 each have a probability of 1/2 at the root. We can draw the root state from a binomial distribution with pstate0 = 0.5.
Once we have a character state for the root, we then simulate evolution along each branch in the tree. We start with the (usually two) branches descending from the root. We then proceed up the tree, branch by branch, until we get to the tips.
We can understand this algorithm perfectly well by thinking about what happens on each branch of the tree, and then extending that algorithm to all of the branches (as described above). For each branch, we first calculate P(t), the transition probability matrix, given the length of the branch and our model of evolution as summarized by Q and the branch length t. We then focus on the row of P(t) that corresponds to the character state at the beginning of the branch. For example, let’s consider a basic two-state Mk model with q = 0.5. We will call the states 0 and 1. We can calculate P(t) for a branch with length t = 3 as:
(eq. 7.16)
\[ \mathbf{P}(t) = e^{\mathbf{Q} t} = exp( \begin{bmatrix} -0.5 & 0.5 \\ 0.5 & -0.5 \\ \end{bmatrix} \cdot 3) = \begin{bmatrix} 0.525 & 0.475 \\ 0.475 & 0.525 \\ \end{bmatrix} \]
If we had started with character state 0 at the beginning of this branch, we would focus on the first row of this matrix. We want to end up at state 0 with probability 0.525 and change to state 1 with probability 0.475. We again draw a uniform random deviate u, and choose state 0 if 0 ≤ u < 0.525 and state 1 if 0.525 ≤ u < 1. If we started with a different character state, we would use a different row in the matrix. If this is an internal branch in the tree, then both daughter species inherit the character state that we chose immediately following speciation – but might diverge soon after! By repeating this along every branch in the tree, we obtain a set of character states at the tips of the tree. This is then the output of our simulation.
Two additional details here are worth noting. First, the procedure for simulating characters under the extended-Mk model are identical to those above, except that the calculation of matrix exponentials is more complicated than in the standard Mk model. Second, if you are simulating a character with more than two states, then the procedure for drawing a random number is slightly different3.
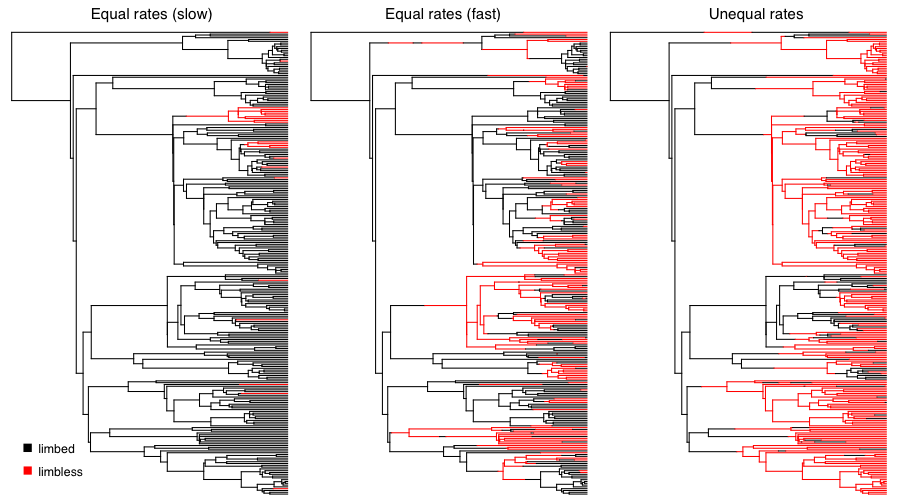
We can apply this approach to simulate the evolution of limblessness in squamates. Below, I present the results of three such simulations. These simulations are a little different than what I describe above because they consider all changes in the tree, rather than just character states at nodes and tips; but the model (and the principal) is the same. You can see that the model leaves an imprint on the pattern of changes in the tree, and you can imagine that one might be able to reconstruct the model using a phylogenetic comparative approach. Of course, typically we know only the tip states, and have to reconstruct changes along branches in the tree. We will discuss parameter estimation for the Mk and extended-Mk models in the next chapter.