3.2: Properties of Brownian Motion
- Page ID
- 21587
We can use Brownian motion to model the evolution of a continuously valued trait through time. Brownian motion is an example of a “random walk” model because the trait value changes randomly, in both direction and distance, over any time interval. The statistical process of Brownian motion was originally invented to describe the motion of particles suspended in a fluid. To me this is a bit hard to picture, but the logic applies equally well to the movement of a large ball over a crowd in a stadium. When the ball is over the crowd, people push on it from many directions. The sum of these many small forces determine the movement of the ball. Again, the movement of the ball can be modeled using Brownian motion 1.
The core idea of this example is that the motion of the object is due to the sum of a large number of very small, random forces. This idea is a key part of biological models of evolution under Brownian motion. It is worth mentioning that even though Brownian motion involves change that has a strong random component, it is incorrect to equate Brownian motion models with models of pure genetic drift (as explained in more detail below).
Brownian motion is a popular model in comparative biology because it captures the way traits might evolve under a reasonably wide range of scenarios. However, perhaps the main reason for the dominance of Brownian motion as a model is that it has some very convenient statistical properties that allow relatively simple analyses and calculations on trees. I will use some simple simulations to show how the Brownian motion model behaves. I will then list the three critical statistical properties of Brownian motion, and explain how we can use these properties to apply Brownian motion models to phylogenetic comparative trees.
When we model evolution using Brownian motion, we are typically discussing the dynamics of the mean character value, which we will denote as $\bar{z}$, in a population. That is, we imagine that you can measure a sample of the individuals in a population and estimate the mean average trait value. We will denote the mean trait value at some time t as $\bar{z}(t)$. We can model the mean trait value through time with a Brownian motion process.
Brownian motion models can be completely described by two parameters. The first is the starting value of the population mean trait, $\bar{z}(0)$. This is the mean trait value that is seen in the ancestral population at the start of the simulation, before any trait change occurs. The second parameter of Brownian motion is the evolutionary rate parameter, σ2. This parameter determines how fast traits will randomly walk through time.
At the core of Brownian motion is the normal distribution. You might know that a normal distribution can be described by two parameters, the mean and variance. Under Brownian motion, changes in trait values over any interval of time are always drawn from a normal distribution with mean 0 and variance proportional to the product of the rate of evolution and the length of time (variance = σ2t). As I will show later, we can simulate change under Brownian motion model by drawing from normal distributions. Another way to say this more simply is that we can always describe how much change to expect under Brownian motion using normal distributions. These normal distributions for expected changes have a mean of zero and get wider as the time interval we consider gets longer.
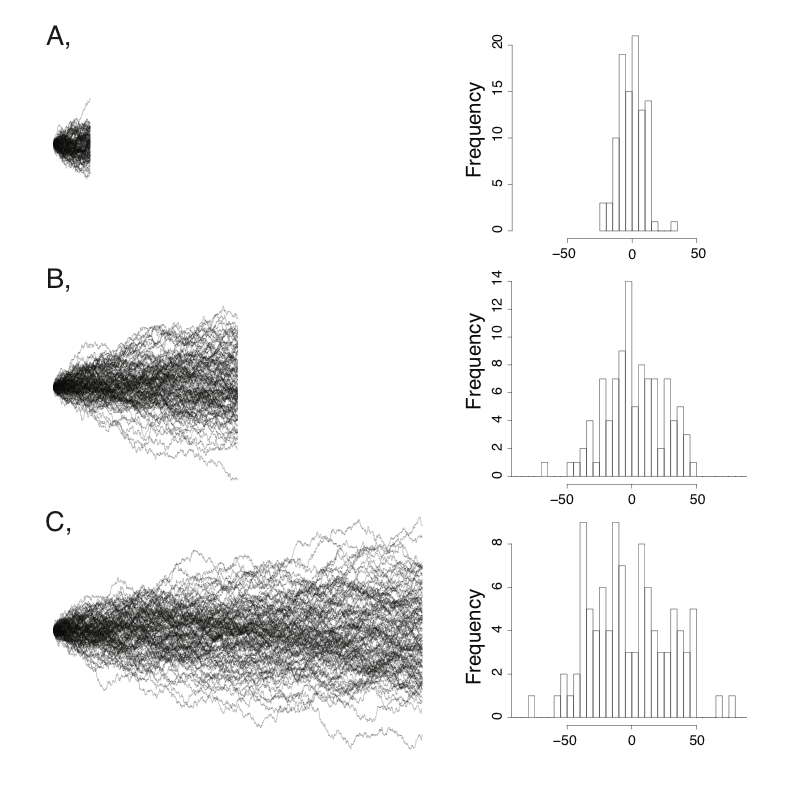
A few simulations will illustrate the behavior of Brownian motion. Figure 3.1 shows sets of Brownian motion run over three different time periods (t = 100, 500, and 1000) with the same starting value $\bar{z}(0) = 0$ and rate parameter σ2 = 1. Each panel of the figure shows 100 simulations of the process over that time period. You can see that the tip values look like normal distributions. Furthermore, the variance among separate runs of the process increases linearly with time. This variance among runs is greatest over the longest time intervals. It is this variance, the variation among many independent runs of the same evolutionary process, that we will consider throughout the next section.
Imagine that we run a Brownian motion process over a given time interval many times, and save the trait values at the end of each of these simulations. We can then create a statistical distribution of these character states. It might not be obvious from figure 3.1, but the distributions of possible character states at any time point in a Brownian walk is normal. This is illustrated in figure 3.2, which shows the distribution of traits from 100,000 simulations with σ2 = 1 and t = 100. The tip characters from all of these simulations follow a normal distribution with mean equal to the starting value, $\bar{z}(0) = 0$, and a variance of σ2t = 100.
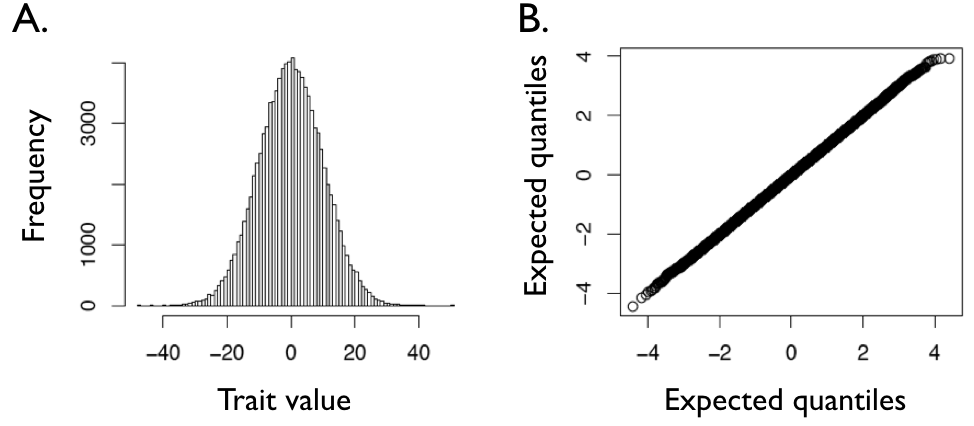
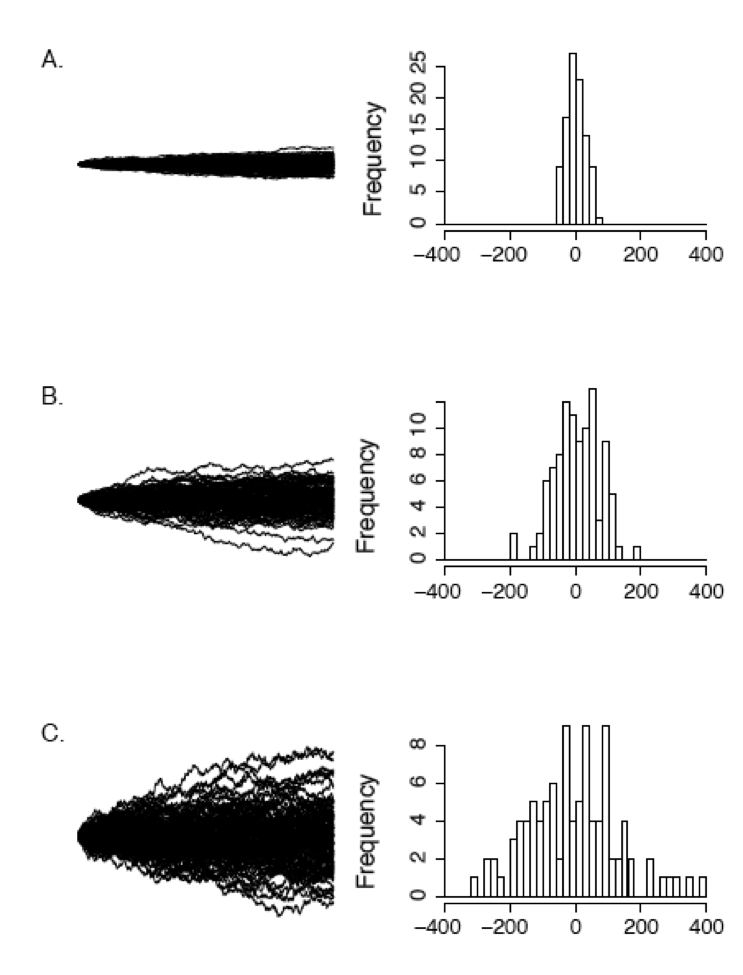
Figure 3.3 shows how rate parameter σ2 affects the rate of spread of Brownian walks. The panels show sets of 100 Brownian motion simulations run over 1000 time units for σ2 = 1 (Panel A), σ2 = 5 (Panel B), and σ2 = 25 (Panel C). You can see that simulations with a higher rate parameter create a larger spread of trait values among simulations over the same amount of time.
If we let \( \bar{z}(t)\) be the value of our character at time t, then we can derive three main properties of Brownian motion. I will list all three, then explain each in turn.
- \(E[\bar{z}(t)] = \bar{z}(0)\)
- Each successive interval of the “walk” is independent
- \(\bar{z}(t) \sim N(\bar{z}(0),\sigma^2 t)\)
First, \( E[\bar{z}(t)] = \bar{z}(0)\). This means that the expected value of the character at any time t is equal to the value of the character at time zero. Here the expected value refers to the mean of \( \bar{z}(t)\) over many replicates. The intuitive meaning of this equation is that Brownian motion has no “trends,” and wanders equally in both positive and negative directions. If you take the mean of a large number of simulations of Brownian motion over any time interval, you will likely get a value close to $\bar{z}(0)$; as you increase the sample size, this mean will tend to get closer and closer to \( \bar{z}(0)\).
Second, each successive interval of the “walk” is independent. Brownian motion is a process in continuous time, and so time does not have discrete “steps.” However, if you sample the process from time 0 to time t, and then again at time t + Δt, the change that occurs over these two intervals will be independent of one another. This is true of any two non-overlapping intervals sampled from a Brownian walk. It is worth noting that only the changes are independent, and that the value of the walk at time t + Δt – which we can write as $\bar{z}(t+\Delta t)$ - is not independent of the value of the walk at time t, \( \bar{z}(t)\). But the differences between successive steps [e.g. \(\bar{z}(t)-\bar{z}(0)\) and \(\bar{z}(t+\Delta t) - \bar{z}(t)\)] are independent of each other and of \( \bar{z}(0)\).
Finally, \( \bar{z}(t) \sim N(\bar{z}(0),\sigma^2 t)\).That is, the value of \( \bar{z}(t)\) is drawn from a normal distribution with mean \( \bar{z}(0)\) and variance σ2t. As we noted above, the parameter σ2 is important for Brownian motion models, as it describes the rate at which the process wanders through trait space. The overall variance of the process is that rate times the amount of time that has elapsed.


