8.6: Testing for Differences in the Forwards and Backwards Rate of Character Change
- Page ID
- 21626
I have been referring to an example of lizard limb evolution throughout this chapter, but we have not yet tested the hypothesis that I stated in the introduction: that transition rates for losing limbs are higher than rates of gaining limbs.
To do this, we can compare our one-rate Mk model with a two-rate model with differences in the rate of forwards and backwards transitions. The character states are 1 (no limbs) and 2 (limbs), and the forward transition represents gaining limbs. This is a special case of the “all-rates different” model discussed in chapter two. Q matrices for these two models will be, for model 1 (equal rates):
\[ \mathbf{Q_{ER}} = \begin{bmatrix} -q & q \\ q & -q \\ \end{bmatrix} \label{8.3A} \]
\[ \mathbf{\pi_{ER}} = \begin{bmatrix} 1/2 & 1/2 \\ \end{bmatrix} \label{8.3B}\]
And for model 2, asymmetric:
\[ \mathbf{Q_{ASY}} = \begin{bmatrix} -q_1 & q_1 \\ q_2 & -q_2 \\ \end{bmatrix} \label{8.4A} \]
\[ \mathbf{\pi_{ASY}} = \begin{bmatrix} 1/2 & 1/2 \\ \end{bmatrix} \label{8.4B} \]
Notice that the ER model has one parameter, while the ASY model has two. Also we have specified equal probabilities of each character at the root of the tree, which may not be justified. But this comparison is still useful as a simple example.
One can compare the two nested models using standard methods discussed in previous chapters – that is, a likelihood-ratio test, AIC, BIC, or other similar methods.
We can apply all of the above methods to analyze the evolution of limblessness in squamates. We can use the tree and character state data from Brandley et al. (2008), which is plotted with ancestral state reconstructions under an ER model in Figure 8.2.
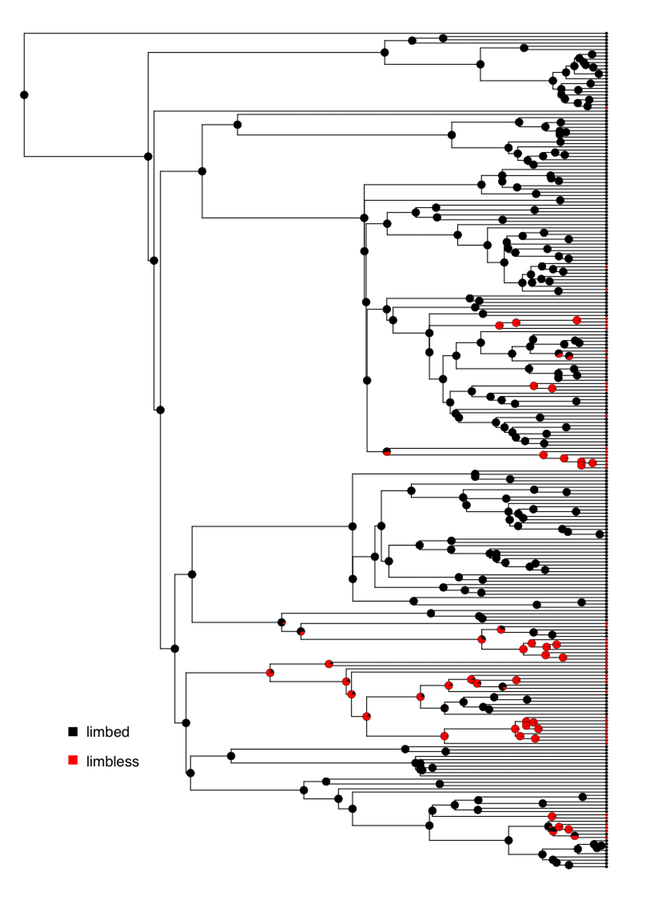
If we fit an Mk model to these data assuming equal state frequencies at the root of the tree, we obtain a lnL of -80.5 and an estimate of the QER matrix as:
\[ \mathbf{Q_{ER}} = \begin{bmatrix} -0.0019 & 0.0019 \\ 0.0019 & -0.0019 \\ \end{bmatrix} \label{8.5}\]
The ASY model with different forward and backward rates gives a lnL of -79.4 and:
\[ \mathbf{Q_{ASY}} = \begin{bmatrix} -0.0016 & 0.0016 \\ 0.0038 & -0.0038 \\ \end{bmatrix} \label{8.6} \]
Note that the ASY model has a higher backwards than forwards rate; as expected, we estimate a rate of losing limbs that is higher than the rate of gaining them (although the difference is surprisingly low). Is this statistically supported? We can compare the AIC scores of the two models. For the ER model, AICc = 163.0, while for the ASY model AICc = 162.8. The AICc score is higher for the unequal rates model, but only by about 0.2 – which is not definitive either way. So based on this analysis, we cannot rule out the possibility that forward and backward rates are equal.
A Bayesian analysis of the ASY model gives similar conclusions (Figure 8.3). We can see that the posterior distribution for the backwards rate (q21) is higher than the forwards rate (q12), but that the two distributions are broadly overlapping.
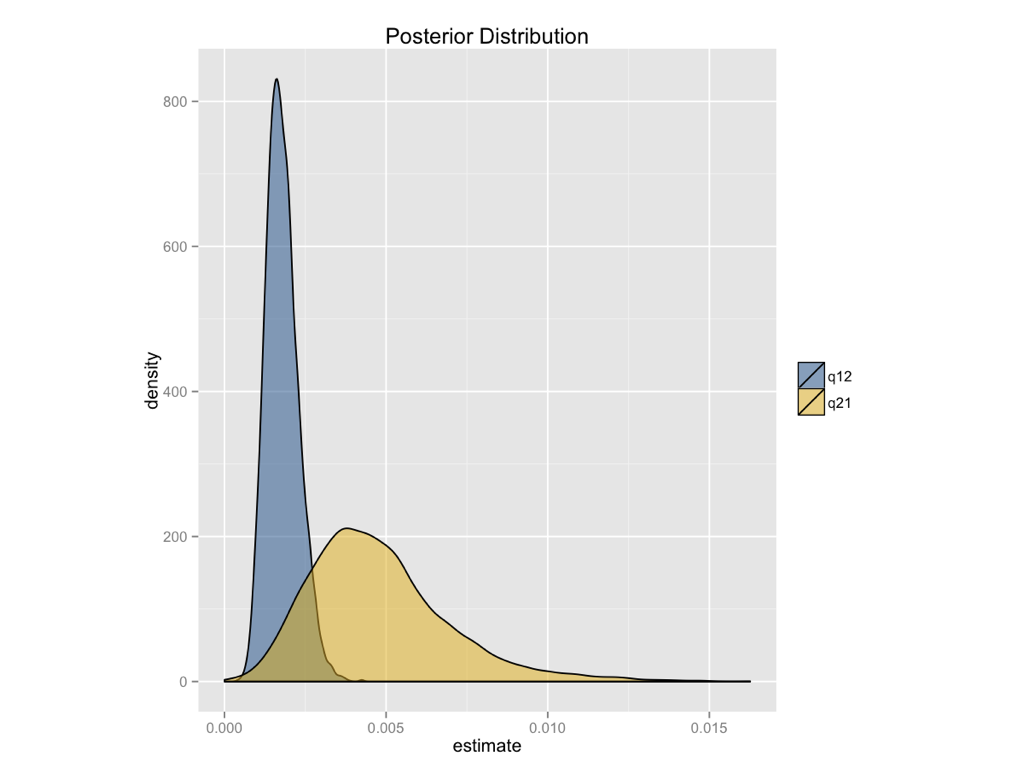
You might wonder about how we can reconcile these results, which suggest that squamates gain limbs at least as frequently as they lose them, with our biological intuition that limbs should be much more difficult to gain than they are to lose. But keep in mind that our comparative analysis is not using any information other than the states of extant species to reconstruct these rates. In particular, identifying irreversible evolution using comparative methods is a problem that is known to be quite difficult, and might require outside information in order to resolve conclusively. For example, if we had some information about the relative number of mutational steps required to gain and lose limbs, we could use an informative prior – which would, I suspect, suggest that limbs are more difficult to gain than they are to lose. Such a prior could dramatically alter the results presented in Figure 8.3. We will return to the problem of irreversible evolution later in the book (Chapter 13).


