5.4: Testing for evolutionary correlations
- Page ID
- 21603
There are many ways to test for evolutionary correlations between two characters. Traditional methods like PICs and PGLS work great for testing evolutionary regression, which is very similar to testing for evolutionary correlations. However, when using those methods the connection to actual models of character evolution can remain opaque. Thus, I will first present approaches to test for correlated evolution based on model selection using AIC and Bayesian analysis. I will then return to “standard” methods for evolutionary regression at the end of the chapter.
Section 5.4a: Testing for character correlations using maximum likelihood and AIC
To test for an evolutionary correlation between two characters, we are really interested in the elements in the matrix R. For two characters, x and y, R can be written as:
(eq. 5.8)
\[ \mathbf{R} = \begin{bmatrix} \sigma_x^2 & \sigma_{xy} \\ \sigma_{xy} & \sigma_y^2 \\ \end{bmatrix} \]
We are interested in the parameter σxy - the evolutionary covariance - and whether it is equal to zero (no correlation) or not. One simple way to test this hypothesis is to set up two competing hypotheses and compare them to each other. One hypothesis (H1) is that the traits evolve independently of each other, and another (H2) that the traits evolve with some covariance σxy. We can write these two rate matrices as:
(eq. 5.9)
\[ \begin{array}{lcr} \mathbf{R}_{H_1} = \begin{bmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2 \\ \end{bmatrix} & \mathbf{R}_{H_2} = \begin{bmatrix} \sigma_x^2 & \sigma_{xy} \\ \sigma_{xy} & \sigma_y^2 \\ \end{bmatrix}\\ \end{array} \]
We can calculate an ML estimate of the parameters in RH2 using equation 5.4. The maximum likelihood estimate of RH1 can be obtained by noting that, if character evolution is independent across all characters, then both σx2 and σy2 can be obtained by treating each character separately and using equations from chapter 3 to solve for each. It turns out that the ML estimates for σx2 and σy2 are always exactly the same for H1 and H2.
To compare these two models, we calculate the likelihood of each using equation 5.4. We can then compare these two likelihoods using either a likelihood ratio test or by comparing AICc scores (see chapter 2).
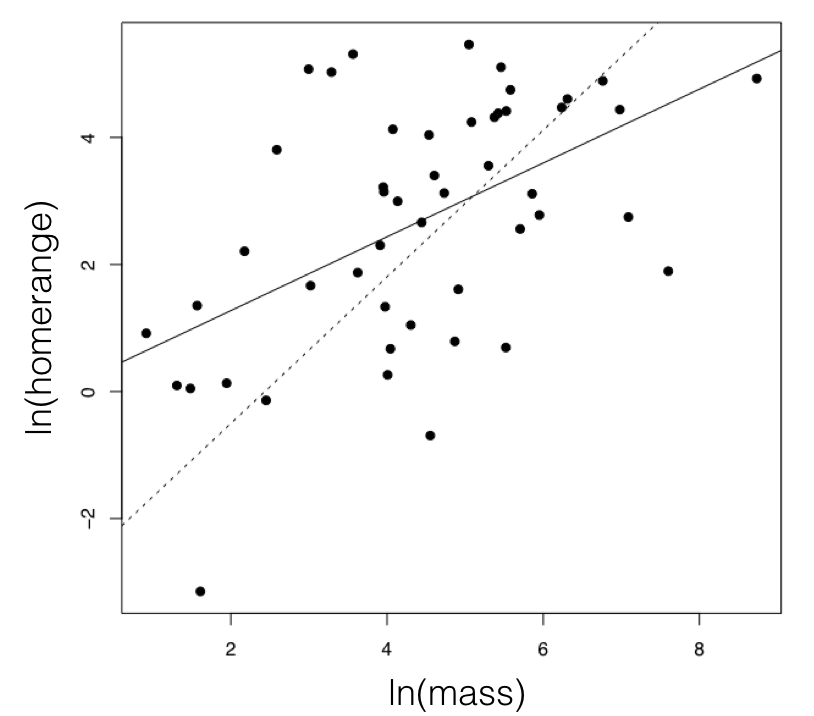
For the mammal example, we can consider the two traits of (ln-transformed) body size and home range size (Garland 1992). These two characters have a positive correlation using standard regression analysis (r = 0.27), and a linear regression is significant (P = 0.0001; Figure 5.3). If we fit a multivariate Brownian motion model to these data, considering home range as trait 1 and body mass as trait 2, we obtain the following parameter estimates:
(eq. 5.10)
\[ \begin{array}{cc} \hat{\mathbf{a}}_{H_2} = \begin{bmatrix} 2.54 \\ 4.64 \\ \end{bmatrix} & \hat{\mathbf{R}}_{H_2} = \begin{bmatrix} 0.24 & 0.10 \\ 0.10 & 0.09 \\ \end{bmatrix}\\ \end{array} \]
Note the positive off-diagonal element in the estimated R matrix, suggesting a positive evolutionary correlation between these two traits. This model corresponds to hypothesis 2 above, and has a log-likelihood of lnL = −164.0. If we fit a model with no correlation between the two traits, we obtain:
(eq. 5.11)
\[ \begin{array}{cc} \hat{\mathbf{a}}_{H_1} = \begin{bmatrix} 2.54 \\ 4.64 \\ \end{bmatrix} & \hat{\mathbf{R}}_{H_1} = \begin{bmatrix} 0.24 & 0 \\ 0 & 0.09 \\ \end{bmatrix}\\ \end{array} \]
It is worth noting again that only the estimates of the evolutionary correlation were affected by this model restriction; all other parameter estimates remain the same. This model has a smaller (more negative) log-likelihood of lnL = −180.5.
A likelihood ratio test gives Δ = 33.0, and P < <0.001, rejecting the null hypothesis. The difference in AICc scores is 30.9, and the Akaike weight for model 2 is effectively 1.0. All ways of comparing these two models give strong support for hypothesis 2. We can conclude that there is an evolutionary correlation between body mass and home range size in mammals. What this means in evolutionary terms is that, across mammals, evolutionary changes in body mass tend to positively covary with changes in home range.
Section 5.4b: Testing for character correlations using Bayesian model selection
We can also implement a Bayesian approach to testing for the correlated evolution of two characters. The simplest way to do this is just to use the standard algorithm for Bayesian MCMC to fit a correlated model to the two characters. We can modify the algorithm presented in chapter 2 as follows:
- Sample a set of starting parameter values σx2, σy2, σxy, $\bar{z}_1(0)$, and $\bar{z}_2 (0)$ from prior distributions. For this example, we can set our prior distribution as uniform between 0 and 1 for σx2 and σy2, uniform from -1 to +1 for σxy, uniform from 1 to 9 for $\bar{z}_1(0)$ (lnMass), and -3 to 5 for $\bar{z}_1(0)$ (lnHomerange).
- Given the current parameter values, select new proposed parameter values using the proposal density Q(p′|p). Here, for all five parameter values, we will use a uniform proposal density with width 0.2, so that Q(p′|p)∼U(p − 0.1, p + 0.1).
- Calculate three ratios:
- The prior odds ratio, Rprior. This is the ratio of the probability of drawing the parameter values p and p’ from the prior. Since our priors are uniform, Rprior = 1.
- The proposal density ratio, Rproposal. This is the ratio of probability of proposals going from p to p’ and the reverse. Our proposal density is symmetrical, so that Q(p′|p)=Q(p|p′) and Rproposal = 1.
- The likelihood ratio, Rlikelihood. This is the ratio of probabilities of the data given the two different parameter values. We can calculate these probabilities from equation 5.6 above (eq. 5.12).
\[ R_{likelihood} = \frac{L(p'|D)}{L(p|D)} = \frac{P(D|p')}{P(D|p)} \[
- Find Raccept, the product of the prior odds, proposal density ratio, and the likelihood ratio. In this case, both the prior odds and proposal density ratios are 1, so Raccept = Rlikelihood.
- Draw a random number x from a uniform distribution between 0 and 1. If x < Raccept, accept the proposed value of all parameters; otherwise reject, and retain the current parameter values.
- Repeat steps 2-5 a large number of times.
We can then inspect the posterior distribution for the parameter is significantly greater than (or less than) zero. As an example, I ran this MCMC for 100,000 generations, discarding the first 10,000 generations as burn-in. I then sampled the posterior distribution every 100 generations, and obtained the following parameter estimates: $\hat{\sigma}_x^2 = 0.26$ [95% credible interval (CI): 0.18 - 0.38], $\hat{\sigma}_y^2 = 0.10$ (95% CI: 0.06 -0.15), and $\hat{\sigma}_{xy} = 0.11$ (95% CI: 0.06 - 0.17; see Figure 5.4). These results are comparable to our ML estimates. Furthermore, the 95% CI for σxy does not overlap with 0; in fact, none of the 901 posterior samples of σxy are less than zero. Again, we can conclude with confidence that there is an evolutionary correlation between these two characters.
Section 5.5c: Testing for character correlations using traditional approaches (PIC, PGLS)
The approach outlined above, which tests for an evolutionary correlation among characters using model selection, is not typically applied in the comparative biology literature. Instead, most tests of character correlation rely on phylogenetic regression using one of two methods: phylogenetic independent contrasts (PICs) and phylogenetic general least squares (PGLS). PGLS is actually mathematically identical to PICs in the simple case described here, and more flexible than PICs for other models and types of characters. Here I will review both PICs and PGLS and explain how they work and how they relate to the models described above.
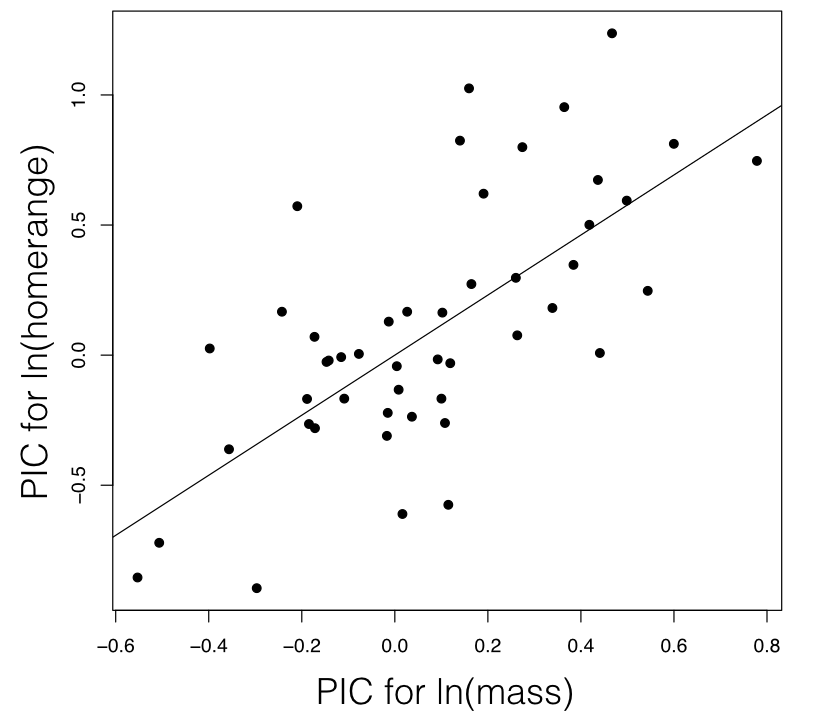
Phylogenetic independent contrasts can be used to carry out a regression test for the relationship between two different characters. To do this, one calculates standardized PICs for trait x and trait y. One then uses standard linear regression forced through the origin to test for a relationship between these two sets of PICs. It is necessary to force the regression through the origin because the direction of subtraction of contrasts across any node in the tree is arbitrary; a reflection of all of the contrasts across both axes simultaneously should have no effect on the analyses3.
For mammal homerange and body mass, a PIC regression test shows a significant correlation between the two traits (P < <0.0001; Figure 5.5).
There is one drawback to PIC regression analysis, though – one does not recover an estimate of the intercept of the regression of y on x – that is, the value of y one would expect when x = 0. The easiest way to get this parameter estimate is to instead use Phylogenetic Generalized Least Squares (PGLS). PGLS uses the common statistical machinery of generalized least squares, and applies it to phylogenetic comparative data. In normal generalized least squares, one constructs a model of the relationship between y and x, as:
(eq. 5.13)
y = XDb + ϵ
Here, y is an n × 1 vector of trait values and b is a vector of unknown regression coefficients that must be estimated from the data. XD is a design matrix including the traits that one wishes to test for a correlation with y and – if the model includes an intercept – a column of 1s. To test for correlations, we use:
(eq. 5.14)
\[ \mathbf{X_D} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \dots & \dots \\ 1 & x_n \\ \end{bmatrix} \]
In the case of one predictor and one response variable, b is 2 × 1 and the resulting model can be used to test correlations between two characters. However, XD could also be multivariate, and can include more than one character that might be related to y. This allows us to carry out the equivalent of multiple regression in a phylogenetic context. Finally, ϵ are the residuals – the difference between the y-values predicted by the model and their actual values. In traditional regression, one assumes that the residuals are all normally distributed with the same variance. By contrast, with GLS, one assumes that the residuals might not be independent of each other; instead, they are multivariate normal with expected mean zero and some variance-covariance matrix Ω.
In the case of Brownian motion, we can model the residuals as having variances and covariances that follow the structure of the phylogenetic tree. In other words, we can substitute our phylogenetic variance-covariance matrix C as the matrix Ω. We can then carry out standard GLS analyses to estimate model parameters:
(eq. 5.15)
\[ \hat{\mathbf{b}} = (\mathbf{X}_D ^ \intercal \mathbf{\Omega}^{-1} \mathbf{X}_D ^ \intercal)^{-1} \mathbf{X}_D ^ \intercal \mathbf{\Omega}^{-1} \mathbf{y} = (\mathbf{X}_D ^ \intercal \mathbf{C}^{-1} \mathbf{X}_D ^ \intercal)^{-1} \mathbf{X}_D ^ \intercal \mathbf{C}^{-1} \mathbf{y} \]
The first term in $\hat{\mathbf{b}}$ is the phylogenetic mean $\bar{z}(0)$. The other term in $\hat{\mathbf{b}}$ will be an estimate for the slope of the relationship between y and x, the calculation of which statistically controls for the effect of phylogenetic relationships.
Applying PGLS to mammal body mass and home range results in an identical estimate of the slope and P-value as we obtain using independent contrasts. PGLS also returns an estimate of the intercept of this relationship, which cannot be obtained from the PICs.
Of course, another difference is that PICs and PGLS use regression, while the approach outlined above tests for a correlation. These two types of statistical tests are different. Correlation tests for a relationship between x and y, while regression tries to find the best way to predict y from x. For correlation, it does not matter which variable we call x and which we call y. However, in regression we will get a different slope if we predict y given x instead of predicting x given y. The model that is assumed by phylogenetic regression models is also different from the model above, where we assumed that the two characters evolve under a correlated Brownian motion model. By contrast, PGLS (and, implicitly, PICs) assume that the deviations of each species from the regression line evolve under a Brownian motion model. We can imagine, for example, that species can freely slide along the regression line, but that evolving around that line can be captured by a normal Brownian model. Another way to think about a PGLS model is that we are treating x as a fixed property of species. The deviation of y from what is predicted by x is what evolves under a Brownian motion model. If this seems strange, that’s because it is! There are other, more complex models for modeling the correlated evolution of two characters that make assumptions that are more evolutionarily realistic (e.g. Hansen 1997); we will return to this topic later in the book. At the same time, PGLS is a well-used method for evolutionary regression, and is undoubtedly useful despite its somewhat strange assumptions.
PGLS analysis, as described above, assumes that we can model the error structure of our linear model as evolving under a Brownian motion model. However, one can change the structure of the error variance-covariance matrix to reflect other models of evolution, such as Ornstein-Uhlenbeck. We return to this topic in a later chapter.


