4.3: Estimating rates using maximum likelihood
- Page ID
- 21594
We can also estimate the evolutionary rate by finding the maximum-likelihood parameter values for a Brownian motion model fit to our data. Recall that ML parameter values are those that maximize the likelihood of the data given our model (see Chapter 2).
We already know that under a Brownian motion model, tip character states are drawn from a multivariate normal distribution with a variance-covariance matrix, C, that is calculated based on the branch lengths and topology of the phylogenetic tree (see Chapter 3). We can calculate the likelihood of obtaining the data under our Brownian motion model using a standard formula for the likelihood of drawing from a multivariate normal distribution:
\[ L(\mathbf{x} | \bar{z}(0), \sigma^2, \mathbf{C}) = \frac {e^{-1/2 (\mathbf{x}-\bar{z}(0) \mathbf{1})^\intercal (\sigma^2 \mathbf{C})^{-1} (\mathbf{x}-\bar{z}(0) \mathbf{1})}} {\sqrt{(2 \pi)^n det(\sigma^2 \mathbf{C})}} \label{4.5} \]
Here, our model parameters are σ2 and \(\bar{z}(0)\), the root trait value. x is an n × 1 vector of trait values for the n tip species in the tree, with species in the same order as C, and 1 is an n × 1 column vector of ones. Note that (σ2C)−1 is the matrix inverse of the matrix σ2C
As an example, with the mammal data, we can calculate the likelihood for a model with parameter values σ2 = 1 and \(\bar{z}(0) = 0\). We need to work with ln-likelihoods (lnL), both because the value here is so small and to facilitate future calculations, so:
\[lnL(\mathbf{x} | \bar{z}(0), \sigma^2, \mathbf{C}) = -116.2.\]
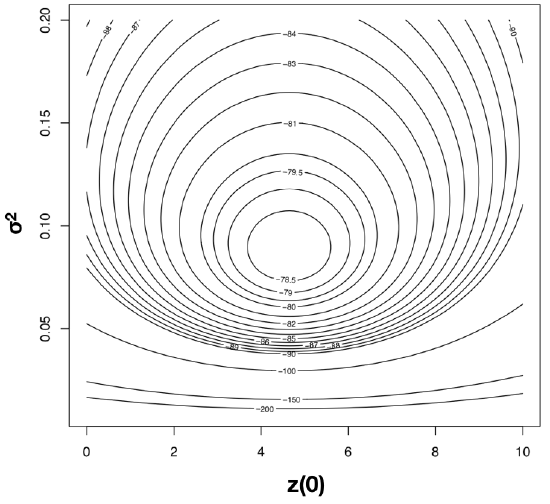
To find the ML estimates of our model parameters, we need to find the parameter values that maximize that function. One (not very efficient) way to do this is to calculate the likelihood across a wide range of parameter values. One can then visualize the resulting likelihood surface and identify the maximum of the likelihood function. For example, the likelihood surface for the mammal body size data given a Brownian motion model is shown in Figure 4.3. Note that this surface has a peak around σ2 = 0.09 and \(\bar{z}(0) = 4\). Inspecting the matrix of ML values, we find the highest ln-likelihood (-78.05) at σ2 = 0.089 and \(\bar{z}(0) = 4.65\).
The calculation described above is inefficient, because we have to calculate likelihoods at a wide range of parameter values that are far from the optimum. A better strategy involves the use of optimization algorithms, a well-developed field of mathematical analysis (Nocedal and Wright 2006). These algorithms differ in their details, but we can illustrate how they work with a general example. Imagine that you are near Mt. St. Helens, and you are tasked with finding the peak of that mountain. It is foggy, but you can see the area around your feet and have an accurate altimeter. One strategy is to simply look at the slope of the mountain where you are standing, and climb uphill. If the slope is steep, you probably still are far from the top, and should climb fast; if the slope is shallow, you might be near the top of the mountain. It may seem obvious that this will get you to a local peak, but perhaps not the highest peak of Mt. St. Helens. Mathematical optimization schemes have this potential difficulty as well, but use some tricks to jump around in parameter space and try to find the overall highest peak as they climb. Details of actual optimization algorithms are beyond the scope of this book; for more information, see Nocedal and Wright (2006).
One simple example is based on Newton’s method of optimization [as implemented, for example, by the r function nlm()]. We can use this algorithm to quickly find accurate ML estimates2.
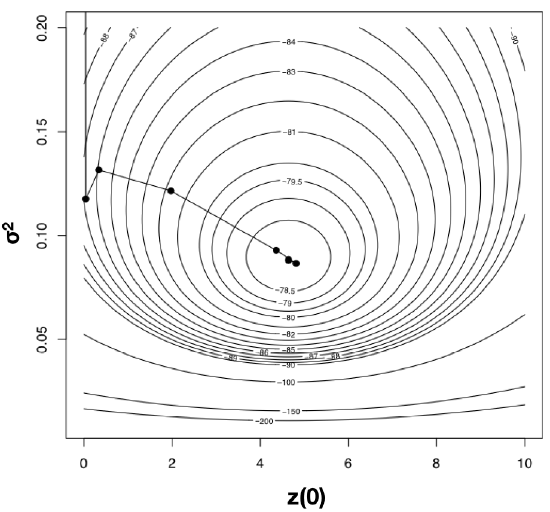
Using optimization algorithms we find a ML solution at \(\hat{\sigma}_{ML}^2 = 0.08804487\) and \(\hat{\bar{z}}(0) = 4.640571\), with lnL = −78.04942. Importantly, the solution can be found with only 10 likelihood calculations; this is the value of good optimization algorithms. I have plotted the path through parameter space taken by Newton’s method when searching for the optimum in Figure 4.4. Notice two things: first, that the function starts at some point and heads uphill on the likelihood surface until an optimum is found; and second, that this calculation requires many fewer steps (and much less time) than calculating the likelihood for a wide range of parameter values.
Using an optimization algorithm also has the added benefit of providing (approximate) confidence intervals for parameter values based on the Hessian of the likelihood surface. This approach assumes that the shape of the likelihood surface in the immediate vicinity of the peak can be approximated by a quadratic function, and uses the curvature of that function, as determined by the Hessian, to approximate the standard errors of parameter values (Burnham and Anderson 2003). If the surface is strongly peaked, the SEs will be small, while if the surface is very broad, the SEs will be large. For example, the likelihood surface around the ML values for mammal body size evolution has a Hessian of:
\[ H = \begin{bmatrix} -314.6 & -0.0026\\ -0.0026 & -0.99 \\ \end{bmatrix} \label{4.6}\]
This gives standard errors of 0.13 (for $\hat{\sigma}_{ML}^2$) and 0.72 [for $\hat{\bar{z}}(0)$]. If we assume the error around these estimates is approximately normal, we can create confidence estimates by adding and subtracting twice the standard error. We then obtain 95% CIs of 0.06 − 0.11 (for \(\hat{\sigma}_{ML}^2\)) and 3.22 − 6.06 [for \(\hat{\bar{z}}(0)\)].
The danger in optimization algorithms is that one can sometimes get stuck on local peaks. More elaborate algorithms repeated for multiple starting points can help solve this problem, but are not needed for simple Brownian motion on a tree as considered here. Numerical optimization is a difficult problem in phylogenetic comparative methods, especially for software developers.
In the particular case of fitting Brownian motion to trees, it turns out that even our fast algorithm for optimization was unnecessary. In this case, the maximum-likelihood estimate for each of these two parameters can be calculated analytically (O’Meara et al. 2006).
\[ \hat{\bar{z}}(0) = (\mathbf{1}^\intercal \mathbf{C}^{-1} \mathbf{1})^{-1} (\mathbf{1}^\intercal \mathbf{C}^{-1} \mathbf{x}) \label{4.7}\]
and:
\[ \hat{\sigma}_{ML}^2 = \frac {(\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})^\intercal \mathbf{C}^{-1} (\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})} {n} \label{4.8}\]
where n is the number of taxa in the tree, C is the n × n variance-covariance matrix under Brownian motion for tip characters given the phylogenetic tree, x is an n × 1 vector of trait values for tip species in the tree, 1 is an n × 1 column vector of ones, $\hat{\bar{z}}(0)$ is the estimated root state for the character, and $\hat{\sigma}_{ML}^2$ is the estimated net rate of evolution.
Applying this approach to mammal body size, we obtain estimates that are exactly the same as our results from numeric optimization: $\hat{\sigma}_{ML}^2 = 0.088$ and \(\hat{\bar{z}}(0) = 4.64\).
Equation (4.8) is biased, and will consistently estimate rates of evolution that are a little too small; an unbiased version based on restricted maximum likelihood (REML) and used by Garland (1992) and others is:
\[ \hat{\sigma}_{REML}^2 = \frac {(\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})^\intercal \mathbf{C}^{-1} (\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})}{n-1} \label{4.9}\]
This correction changes our estimate of the rate of body size in mammals from \(\hat{\sigma}_{ML}^2 = 0.088\) to \(\hat{\sigma}_{REML}^2 = 0.090\). Equation \ref{4.8} is exactly identical to the estimated rate of evolution calculated using the average squared independent contrast, described above; that is, \(\hat{\sigma}_{PIC}^2 = \hat{\sigma}_{REML}^2\). In fact, PICs are a formulation of a REML model. The “restricted” part of REML refers to the fact that these methods calculate likelihoods based on a transformed set of data where the effect of nuisance parameters has been removed. In this case, the nuisance parameter is the estimated root state \(\hat{\bar{z}}(0)\) 3.
For the mammal body size example, we can further explore the difference between REML and ML in terms of statistical confidence intervals using likelihoods based on the contrasts. We assume, again, that the contrasts are all drawn from a normal distribution with mean 0 and unknown variance. If we again use Newton’s method for optimization, we find a maximum REML log-likelihood of -10.3 at \(\hat{\sigma}_{REML}^2 = 0.090\). This returns a 1 × 1 matrix for the Hessian with a value of 2957.8, corresponding to a SE of 0.018. This slightly larger SE corresponds to 95% CI for \(\hat{\sigma}_{REML}^2\) of 0.05 − 0.13.
In the context of comparative methods, REML has two main advantages. First, PICs treat the root state of the tree as a nuisance parameter. We typically have very little information about this root state, so that can be an advantage of the REML approach. Second, PICs are easy to calculate for very large phylogenetic trees because they do not require the construction (or inversion!) of any large variance-covariance matrices. This is important for big phylogenetic trees. Imagine that we had a phylogenetic tree of all vertebrates (~60,000 species) and wanted to calculate the rate of body size evolution. To use standard maximum likelihood, we have to calculate C, a matrix with 60, 000 × 60, 000 = 3.6 billion entries, and invert it to calculate C−1. To calculate PICs, by contrast, we only have to carry out on the order of 120,000 operations. Thankfully, there are now pruning algorithms to quickly calculate likelihoods for large trees under a variety of different models (see, e.g., FitzJohn 2012; Freckleton 2012; and Ho and Ané 2014).


