7.3: Markov Chains and HMMS - From Example to Formalizing

Last updated
Save as PDF

Page ID: 40954

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Motivating Example: Weather Prediction

Weather prediction has always been difficult, especially when we would like to forecast the weather many days, weeks or even months later. However, if we only need to predict the weather of the next day, we can reach decent prediction precision using some quite simple models such as Markov Chain and Hidden Markov Model by building graphical models in Figure 7.2.

Figure 7.2: Prediction Models Using Markov Chain and HMM © source unknown. All rights reserved. This content is excluded from our Creative Commons license. For more information, see http://ocw.mit.edu/help/faq-fair-use/.

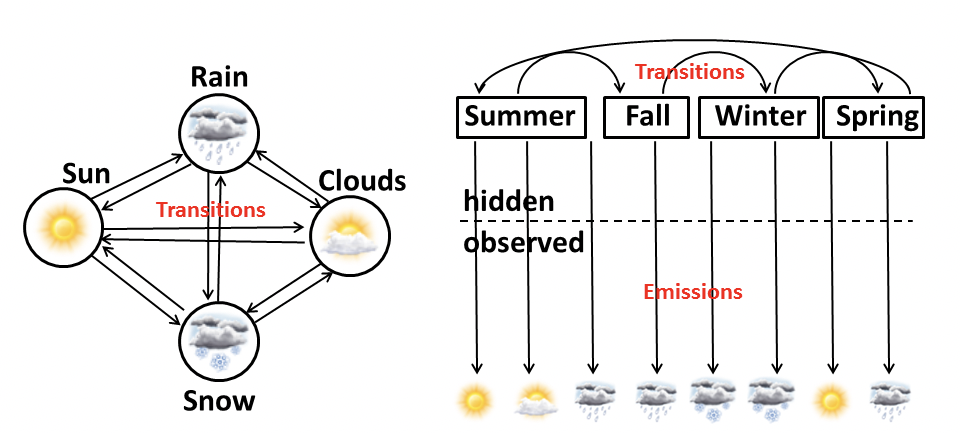
For the Markov Chain model on the left, four kinds of weather (Sun, Rain, Clouds and Snow) can directly transition from one to the other. This is a “what you see is what you get” in that the next state only depends on the current state and there is no memory of the previous state. However for HMM on the right, all the types of weather are modeled as the emission(or outcome) of the hidden seasons (Summer, Fall, Winter and Spring). The key insight behind is that the hidden states of the world (e.g. season or storm system) determines emission probabilities while state transitions are governed by a Markov Chain.

Formalizing of Markov Chain and HMMS

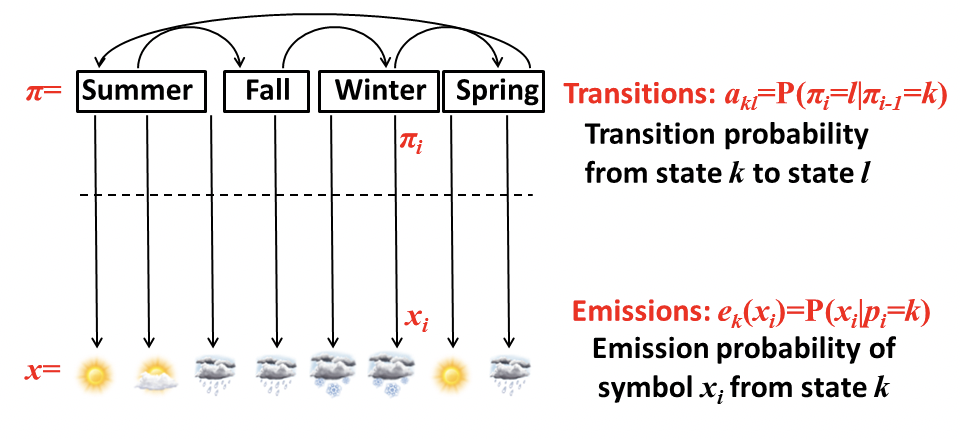
To take a closer look at Hidden Markov Model, let’s first define the key parameters in Figure 7.3. Vector x represents sequence of observations. Vector π represents the hidden path, which is the sequence of hidden states. Each entry a_kl of Transition matrix A denotes the probability of transition from state k to state l. Each entry e_k(x_i) of emission vector denotes the probability of observing x_i from state k. And finally with these parameters and Bayes’s rule, we can use p(x_i|π_i = k) to estimate p(π_i = k|x_i).

Markov Chains

A Markov Chain is given by a finite set of states and transition probabilities between the states. At every time step, the Markov Chain is in a particular state and undergoes a transition to another state. The probability of transitioning to each other state depends only on the current state, and in particular is independent of how the current state was reached. More formally, a Markov Chain is a triplet (Q, p, A) which consists of:

Figure 7.3: Parameterization of HMM Prediction Model. © source unknown. All rights reserved. This content is excluded from our Creative Commons license. For more information, see http://ocw.mit.edu/help/faq-fair-use/.

A set of states Q.

A transition matrix A whose elements correspond to the probability Aij of transitioning from state i to state j.
A vector p of initial state probabilities.

The key property of Markov Chains is that they are memory-less, i.e., each state depends only on the previous state. So we can immediately define a probability for the next state, given the current state:

\[P\left(x_{i} \mid x_{i-1}, \ldots, x_{1}\right)=P\left(x_{i} \mid x _{i-1}\right)\]

In this way, the probability of the sequence can be decomposed as follows:

\[P (x) = P (x_L, x_{L−1}, ..., x_1) = P (x_L|x_{L−1})P (x_{L−1}|x_{L−2})...P (x_2|x_1)P (x_1)\]

\(P(xL)\) can also be calculated from the transition probabilities: If we multiply the initial state probabilities at time t = 0 by the transition matrix A, we get the probabilities of states at time t = 1. Multiplying by the appropriate power AL of the transition matrix, we obtain the state probabilities at time t = L.

Hidden Markov Models

Hidden Markov Models are used as a representation of a problem space in which observations come about as a result of states of a system which we are unable to observe directly. These observations, or emissions, result from a particular state based on a set of probabilities. Thus HMMs are Markov Models where the states are hidden from the observer and instead we have observations generated with certain probabilities associated with each state. These probabilities of observations are known as emission probabilities.

Formally, a Hidden Markov Model is a 5-tuple (Q, A, p, V , E) which consists of the following parameters:

A series of states, Q.
A transition matrix, A
A vector of initial state probabilities , p.
A set of observation symbols, V , for example {A, T, C, G} or the set of amino acids or words in an English dictionary.
A matrix of emission probabilities, E: For each s, t, in Q, the emission probability is e_sk = P(v_k at time t|q_t = s)

The key property of memorylessness is inherited from Markov Models. The emissions and transitions depend only on the current state and not on the past history.