3.3: Enzyme Kinetics
- Page ID
- 16102
Unlike uncatalyzed (but readily occurring) reactions, in which the rate of the reaction is dependent only on the concentration of the reactants, the rate of enzyme-catalyzed reactions is limited by the number of enzyme molecules available. This maximal rate of turnover from substrate to product is a function of the speed of the enzyme and the number of enzyme molecules. \(V_{max}\), this theoretical maximal rate or reaction, is approached when there is such a high concentration of substrate molecules that not only is every available enzyme at a given time occupied, but as soon as an enzyme finishes converting substrate to product, it immediately binds a new substrate. Another term, Km, is related to \(V_{max}\) in that \(K_m\) (the Michaelis constant) is the concentration of substrate at which half-maximal reaction rate \(V_{max}/2\) occurs. These two terms are related in the Michaelis-Menten equation, which describes the reaction rate \(v\) with respect to the substrate concentration [S].
\[v = \frac { V _ { \max } [ \mathrm { S } ] } { \mathrm { K } _ { \mathrm { M } } + [ \mathrm { S } ] } \label{Michaelis-Menten}\]
The Michaelis-Menten equation was derived by Leonor Michaelis and his graduate student Maud Menten in 1913, based on work by Victor Henri, and is applicable only to simple enzyme kinetics in which there is only one substrate that is changed immediately to a product during the reaction without forming any intermediate compound, the enzyme in question shows no allostericity, and the reaction is unidirectional.
It should be noted that the reaction rate v is actually the initial reaction rate at a particular substrate concentration, and is sometimes denoted vo. Naturally, as the reaction continues, the substrate concentration decreases, along with the reaction rate.
The Michaelis-Menten equation assumes a simple reaction of the form:
\[\ce{E + S <=> ES -> E +P}\]
where \(E\) is an enzyme, \(S\) is the substrate, and \(P\) is the product. Note the formation of the intermediate enzyme-substrate complex, ES, which is a transition state (recall Figure \(\PageIndex{2}\)) in which the substrate is unstable and associated with the enzyme. In fact, \(ES\) could as easily be considered \(EP\), since this state is essentially the tipping point between the conversion from substrate to product. In this construction, the Michaelis constant, \(K_M\), of an enzyme-catalyzed reaction is (k2 + k3)/k1. That is the rate of ES dissociation over the rate of ES association. \(K_M\), of course, varies not only depending on the enzyme, but also with respect to the identity of the substrate. Some enzymes can work with multiple substrates, and the \(K_M\) of that enzyme for the different substrates is usually different. Because the saturation curve in Figure \(\PageIndex{5}\) can be difficult to work with, linearizations of the Michaelis-Menten equation (Equation \ref{Michaelis-Menten}) were developed. The most common is the double reciprocal plot, better known as the Lineweaver-Burk plot. On this type of graphical representation of enzyme kinetics, the reciprocal of the substrate concentration is plotted against the reciprocal of the reaction velocity. This generates a line in which the x-intercept is then \(-1/K_m\), the y-intercept is \(1/V_{max}\), and the slope of the line is \(K_m/V_{max}\).
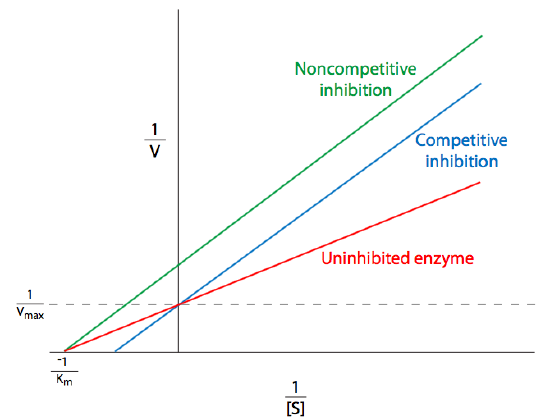
Obtaining \(V_{max}\) and \(K_m\) from a direct plot of v against [S] can be difficult because even at very high substrate concentrations, experimental data may still be significantly under the \(V_{max}\). This leads to underestimation of the Vmax.
The Lineweaver-Burk plot addresses this concern, but has some shortcomings of its own. Because it is easier to obtain data at high concentrations, most of the data points are near 0, and fewer data points are available further out (to the right of the graph). Because these are reciprocals, under these low [S] conditions, small errors in measured values of \(v\) turn into large errors in 1/v, and therefore large errors in \(K_M\) and Vmax. This is evident on examination of the Lineweaver-Burk equation:
\[\frac { 1 } { v } = \left( \frac { K _ { M } } { V _ { \max } } \right) \frac { 1 } { [ S ] } + \frac { 1 } { V _ { \max } }\]


